Loading AI tools
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic (or Euler number, or Euler–Poincaré characteristic) is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent. It is commonly denoted by (Greek lower-case letter chi).
The Euler characteristic was originally defined for polyhedra and used to prove various theorems about them, including the classification of the Platonic solids. It was stated for Platonic solids in 1537 in an unpublished manuscript by Francesco Maurolico.[1] Leonhard Euler, for whom the concept is named, introduced it for convex polyhedra more generally but failed to rigorously prove that it is an invariant. In modern mathematics, the Euler characteristic arises from homology and, more abstractly, homological algebra.

The Euler characteristic χ was classically defined for the surfaces of polyhedra, according to the formula
where V, E, and F are respectively the numbers of vertices (corners), edges and faces in the given polyhedron. Any convex polyhedron's surface has Euler characteristic
This equation, stated by Euler in 1758,[2] is known as Euler's polyhedron formula.[3] It corresponds to the Euler characteristic of the sphere (i.e. ), and applies identically to spherical polyhedra. An illustration of the formula on all Platonic polyhedra is given below.
| Name | Image | Vertices V | Edges E | Faces F |
Euler characteristic: |
|---|---|---|---|---|---|
| Tetrahedron |  | 4 | 6 | 4 | 2 |
| Hexahedron or cube |  | 8 | 12 | 6 | 2 |
| Octahedron |  | 6 | 12 | 8 | 2 |
| Dodecahedron | 20 | 30 | 12 | 2 | |
| Icosahedron |  | 12 | 30 | 20 | 2 |
The surfaces of nonconvex polyhedra can have various Euler characteristics:
| Name | Image | Vertices V | Edges E | Faces F |
Euler characteristic: |
|---|---|---|---|---|---|
| Tetrahemihexahedron |  | 6 | 12 | 7 | 1 |
| Octahemioctahedron |  | 12 | 24 | 12 | 0 |
| Cubohemioctahedron |  | 12 | 24 | 10 | −2 |
| Small stellated dodecahedron |  | 12 | 30 | 12 | −6 |
| Great stellated dodecahedron |  | 20 | 30 | 12 | 2 |
For regular polyhedra, Arthur Cayley derived a modified form of Euler's formula using the density D, vertex figure density and face density
This version holds both for convex polyhedra (where the densities are all 1) and the non-convex Kepler–Poinsot polyhedra.
Projective polyhedra all have Euler characteristic 1, like the real projective plane, while the surfaces of toroidal polyhedra all have Euler characteristic 0, like the torus.
Plane graphs
The Euler characteristic can be defined for connected plane graphs by the same formula as for polyhedral surfaces, where F is the number of faces in the graph, including the exterior face.
The Euler characteristic of any plane connected graph G is 2. This is easily proved by induction on the number of faces determined by G, starting with a tree as the base case. For trees, and If G has C components (disconnected graphs), the same argument by induction on F shows that One of the few graph theory papers of Cauchy also proves this result.
Via stereographic projection the plane maps to the 2-sphere, such that a connected graph maps to a polygonal decomposition of the sphere, which has Euler characteristic 2. This viewpoint is implicit in Cauchy's proof of Euler's formula given below.
Proof of Euler's formula

There are many proofs of Euler's formula. One was given by Cauchy in 1811, as follows. It applies to any convex polyhedron, and more generally to any polyhedron whose boundary is topologically equivalent to a sphere and whose faces are topologically equivalent to disks.
Remove one face of the polyhedral surface. By pulling the edges of the missing face away from each other, deform all the rest into a planar graph of points and curves, in such a way that the perimeter of the missing face is placed externally, surrounding the graph obtained, as illustrated by the first of the three graphs for the special case of the cube. (The assumption that the polyhedral surface is homeomorphic to the sphere at the beginning is what makes this possible.) After this deformation, the regular faces are generally not regular anymore. The number of vertices and edges has remained the same, but the number of faces has been reduced by 1. Therefore, proving Euler's formula for the polyhedron reduces to proving for this deformed, planar object.
If there is a face with more than three sides, draw a diagonal—that is, a curve through the face connecting two vertices that are not yet connected. Each new diagonal adds one edge and one face and does not change the number of vertices, so it does not change the quantity (The assumption that all faces are disks is needed here, to show via the Jordan curve theorem that this operation increases the number of faces by one.) Continue adding edges in this manner until all of the faces are triangular.
Apply repeatedly either of the following two transformations, maintaining the invariant that the exterior boundary is always a simple cycle:
- Remove a triangle with only one edge adjacent to the exterior, as illustrated by the second graph. This decreases the number of edges and faces by one each and does not change the number of vertices, so it preserves
- Remove a triangle with two edges shared by the exterior of the network, as illustrated by the third graph. Each triangle removal removes a vertex, two edges and one face, so it preserves
These transformations eventually reduce the planar graph to a single triangle. (Without the simple-cycle invariant, removing a triangle might disconnect the remaining triangles, invalidating the rest of the argument. A valid removal order is an elementary example of a shelling.)
At this point the lone triangle has and so that Since each of the two above transformation steps preserved this quantity, we have shown for the deformed, planar object thus demonstrating for the polyhedron. This proves the theorem.
For additional proofs, see Eppstein (2013).[4] Multiple proofs, including their flaws and limitations, are used as examples in Proofs and Refutations by Lakatos (1976).[5]
The polyhedral surfaces discussed above are, in modern language, two-dimensional finite CW-complexes. (When only triangular faces are used, they are two-dimensional finite simplicial complexes.) In general, for any finite CW-complex, the Euler characteristic can be defined as the alternating sum
where kn denotes the number of cells of dimension n in the complex.
Similarly, for a simplicial complex, the Euler characteristic equals the alternating sum
where kn denotes the number of n-simplexes in the complex.
Betti number alternative
More generally still, for any topological space, we can define the nth Betti number bn as the rank of the n-th singular homology group. The Euler characteristic can then be defined as the alternating sum
This quantity is well-defined if the Betti numbers are all finite and if they are zero beyond a certain index n0. For simplicial complexes, this is not the same definition as in the previous paragraph but a homology computation shows that the two definitions will give the same value for .
The Euler characteristic behaves well with respect to many basic operations on topological spaces, as follows.
Homotopy invariance
Homology is a topological invariant, and moreover a homotopy invariant: Two topological spaces that are homotopy equivalent have isomorphic homology groups. It follows that the Euler characteristic is also a homotopy invariant.
For example, any contractible space (that is, one homotopy equivalent to a point) has trivial homology, meaning that the 0th Betti number is 1 and the others 0. Therefore, its Euler characteristic is 1. This case includes Euclidean space of any dimension, as well as the solid unit ball in any Euclidean space — the one-dimensional interval, the two-dimensional disk, the three-dimensional ball, etc.
For another example, any convex polyhedron is homeomorphic to the three-dimensional ball, so its surface is homeomorphic (hence homotopy equivalent) to the two-dimensional sphere, which has Euler characteristic 2. This explains why the surface of a convex polyhedron has Euler characteristic 2.
Inclusion–exclusion principle
If M and N are any two topological spaces, then the Euler characteristic of their disjoint union is the sum of their Euler characteristics, since homology is additive under disjoint union:
More generally, if M and N are subspaces of a larger space X, then so are their union and intersection. In some cases, the Euler characteristic obeys a version of the inclusion–exclusion principle:
This is true in the following cases:
- if M and N are an excisive couple. In particular, if the interiors of M and N inside the union still cover the union.[6]
- if X is a locally compact space, and one uses Euler characteristics with compact supports, no assumptions on M or N are needed.
- if X is a stratified space all of whose strata are even-dimensional, the inclusion–exclusion principle holds if M and N are unions of strata. This applies in particular if M and N are subvarieties of a complex algebraic variety.[7]
In general, the inclusion–exclusion principle is false. A counterexample is given by taking X to be the real line, M a subset consisting of one point and N the complement of M.
Connected sum
For two connected closed n-manifolds one can obtain a new connected manifold via the connected sum operation. The Euler characteristic is related by the formula [8]
Product property
Also, the Euler characteristic of any product space M × N is
These addition and multiplication properties are also enjoyed by cardinality of sets. In this way, the Euler characteristic can be viewed as a generalisation of cardinality; see .
Covering spaces
Similarly, for a k-sheeted covering space one has
More generally, for a ramified covering space, the Euler characteristic of the cover can be computed from the above, with a correction factor for the ramification points, which yields the Riemann–Hurwitz formula.
Fibration property
The product property holds much more generally, for fibrations with certain conditions.
If is a fibration with fiber F, with the base B path-connected, and the fibration is orientable over a field K, then the Euler characteristic with coefficients in the field K satisfies the product property:[9]
This includes product spaces and covering spaces as special cases, and can be proven by the Serre spectral sequence on homology of a fibration.
For fiber bundles, this can also be understood in terms of a transfer map – note that this is a lifting and goes "the wrong way" – whose composition with the projection map is multiplication by the Euler class of the fiber:[10]
Surfaces
The Euler characteristic can be calculated easily for general surfaces by finding a polygonization of the surface (that is, a description as a CW-complex) and using the above definitions.
| Name | Image | χ |
|---|---|---|
| Interval |  |
1 |
| Circle |  |
0 |
| Disk |  |
1 |
| Sphere |  |
2 |
| Torus (Product of two circles) |
 |
0 |
| Double torus |  |
−2 |
| Triple torus |  |
−4 |
| Real projective plane |
 |
1 |
| Möbius strip | 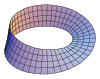 |
0 |
| Klein bottle | 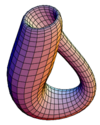 |
0 |
| Two spheres (not connected) (Disjoint union of two spheres) |
 |
2 + 2 = 4 |
| Three spheres (not connected) (Disjoint union of three spheres) |
   |
2 + 2 + 2 = 6 |
| spheres (not connected) (Disjoint union of n spheres) |
 . . . . . .  |
2 + ... + 2 = 2n |
Soccer ball
It is common to construct soccer balls by stitching together pentagonal and hexagonal pieces, with three pieces meeting at each vertex (see for example the Adidas Telstar). If P pentagons and H hexagons are used, then there are faces, vertices, and edges. The Euler characteristic is thus
Because the sphere has Euler characteristic 2, it follows that That is, a soccer ball constructed in this way always has 12 pentagons. The number of hexagons can be any nonnegative integer except 1.[11] This result is applicable to fullerenes and Goldberg polyhedra.
Arbitrary dimensions

The n dimensional sphere has singular homology groups equal to
hence has Betti number 1 in dimensions 0 and n, and all other Betti numbers are 0. Its Euler characteristic is then χ = 1 + (−1) n ; that is, either 0 if n is odd, or 2 if n is even.
The n dimensional real projective space is the quotient of the n sphere by the antipodal map. It follows that its Euler characteristic is exactly half that of the corresponding sphere – either 0 or 1.
The n dimensional torus is the product space of n circles. Its Euler characteristic is 0, by the product property. More generally, any compact parallelizable manifold, including any compact Lie group, has Euler characteristic 0.[12]
The Euler characteristic of any closed odd-dimensional manifold is also 0.[13] The case for orientable examples is a corollary of Poincaré duality. This property applies more generally to any compact stratified space all of whose strata have odd dimension. It also applies to closed odd-dimensional non-orientable manifolds, via the two-to-one orientable double cover.
The Euler characteristic of a closed orientable surface can be calculated from its genus g (the number of tori in a connected sum decomposition of the surface; intuitively, the number of "handles") as
The Euler characteristic of a closed non-orientable surface can be calculated from its non-orientable genus k (the number of real projective planes in a connected sum decomposition of the surface) as
For closed smooth manifolds, the Euler characteristic coincides with the Euler number, i.e., the Euler class of its tangent bundle evaluated on the fundamental class of a manifold. The Euler class, in turn, relates to all other characteristic classes of vector bundles.
For closed Riemannian manifolds, the Euler characteristic can also be found by integrating the curvature; see the Gauss–Bonnet theorem for the two-dimensional case and the generalized Gauss–Bonnet theorem for the general case.
A discrete analog of the Gauss–Bonnet theorem is Descartes' theorem that the "total defect" of a polyhedron, measured in full circles, is the Euler characteristic of the polyhedron.
Hadwiger's theorem characterizes the Euler characteristic as the unique (up to scalar multiplication) translation-invariant, finitely additive, not-necessarily-nonnegative set function defined on finite unions of compact convex sets in ℝn that is "homogeneous of degree 0".
For every combinatorial cell complex, one defines the Euler characteristic as the number of 0-cells, minus the number of 1-cells, plus the number of 2-cells, etc., if this alternating sum is finite. In particular, the Euler characteristic of a finite set is simply its cardinality, and the Euler characteristic of a graph is the number of vertices minus the number of edges. (Olaf Post calls this a "well-known formula".[14])
More generally, one can define the Euler characteristic of any chain complex to be the alternating sum of the ranks of the homology groups of the chain complex, assuming that all these ranks are finite.[15]
A version of Euler characteristic used in algebraic geometry is as follows. For any coherent sheaf on a proper scheme X, one defines its Euler characteristic to be
where is the dimension of the i-th sheaf cohomology group of . In this case, the dimensions are all finite by Grothendieck's finiteness theorem. This is an instance of the Euler characteristic of a chain complex, where the chain complex is a finite resolution of by acyclic sheaves.
Another generalization of the concept of Euler characteristic on manifolds comes from orbifolds (see Euler characteristic of an orbifold). While every manifold has an integer Euler characteristic, an orbifold can have a fractional Euler characteristic. For example, the teardrop orbifold has Euler characteristic 1 + 1/ p , where p is a prime number corresponding to the cone angle 2π / p .
The concept of Euler characteristic of the reduced homology of a bounded finite poset is another generalization, important in combinatorics. A poset is "bounded" if it has smallest and largest elements; call them 0 and 1. The Euler characteristic of such a poset is defined as the integer μ(0,1), where μ is the Möbius function in that poset's incidence algebra.
This can be further generalized by defining a rational valued Euler characteristic for certain finite categories, a notion compatible with the Euler characteristics of graphs, orbifolds and posets mentioned above. In this setting, the Euler characteristic of a finite group or monoid G is 1/ | G | , and the Euler characteristic of a finite groupoid is the sum of 1/ |Gi |, where we picked one representative group Gi for each connected component of the groupoid.[16]
Wikiwand in your browser!
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.




 ...
...





























 ...
...




 ...
...






