The Fifty-Nine Icosahedra

The Fifty-Nine Icosahedra is a book written and illustrated by H. S. M. Coxeter, P. Du Val, H. T. Flather and J. F. Petrie. It enumerates certain stellations of the regular convex or Platonic icosahedron, according to a set of rules put forward by J. C. P. Miller.

The stellation diagram for the icosahedron with the central triangle marked for the original icosahedron

First published by the University of Toronto in 1938, a Second Edition reprint by Springer-Verlag followed in 1982. Tarquin's 1999 Third Edition included new reference material and photographs by K. and D. Crennell.

Stellating polyhedra

Main article: Stellation

Notable stellations of the icosahedron
Regular	Regular star	Uniform duals
(Convex) icosahedron	Great icosahedron	Small triambic icosahedron	Medial triambic icosahedron	Great triambic icosahedron
Regular compounds			Others
Compound of five octahedra	Compound of five tetrahedra	Compound of ten tetrahedra	Excavated dodecahedron	Final stellation

A polyhedron is stellated by extending the face planes of a polyhedron until they meet again to form a new polyhedron or compound. The interior of the new polyhedron is divided by the face planes into a number of cells. When extended indefinitely, the face planes of a polyhedron may divide space into a great many such cells. Different cell sets then yield different stellations.

For a symmetrical polyhedron, these cells will fall into groups, or sets, of congruent cells – we say that the cells in such a congruent set are of the same type. This can still lead to a large number of possible forms, so further criteria are often imposed to reduce the set to those stellations that are significant and unique in some way.

A set of cells forming a closed layer around its core is called a shell. A shell may be made up of one or more cell types.

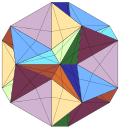
Among the Platonic solids, the tetrahedron and cube have no stellations, the octahedron has one (stella octangula), the dodecahedron has three (small stellated dodecahedron, great dodecahedron and great stellated dodecahedron) and the icosahedron has a much larger number.

Earlier publications on stellated icosahedra

The Fifty-Nine Icosahedra is not the first work about stellated icosahedra.

In 1809 Louis Poinsot discovered the first recognised examples, the great icosahedron (G in the list below) and the great dodecahedron, completing the set of what are nowadays known as the regular star or Kepler–Poinsot polyhedra.^[1]

In 1876 Edmund Hess used stellation diagrams and discovered the remaining mainline stellated icosahedra. (B to F and H in the list below) ^[2][3]

In 1900 Max Brückner described and photographed many stellated icosahedra in his book Vielecke und Vielflache: Theorie und Geschichte (Polygons and polyhedra: Theory and History, Leipzig: B. G. Teubner, 1900).^[4]

In 1924 A. Harry Wheeler gave a talk as an Invited Speaker of the ICM in 1924 at Toronto.^[5] In his talk he presented the method of selecting regions of the stellation diagram and combining their cells to form new polyhedral figures. Wheeler included hollow polyhedra and sets of discrete (non connected) cells. Wheeler was initially to be a co-author of The Fifty-Nine Icosahedra, but he objected to Coxeter's approach, which he found so “involved and clumsy that I did not want to have anything to do with it. ... Coxeter has a way of taking a subject and tying it up into knots in such a way that I find it quite difficult to follow him and some times to even make sense.”^[6]

Authors' contributions

Miller's rules

Although Miller did not contribute to the book directly, he was a close colleague of Coxeter and Petrie. His contribution is immortalised in his set of rules for defining which stellation forms should be considered "properly significant and distinct":

(i) The faces must lie in twenty planes, viz., the bounding planes of the regular icosahedron.

(ii) All parts composing the faces must be the same in each plane, although they may be quite disconnected.

(iii) The parts included in any one plane must have trigonal symmetry, without or with reflection. This secures icosahedral symmetry for the whole solid.

(iv) The parts included in any plane must all be "accessible" in the completed solid (i.e. they must be on the "outside". In certain cases we should require models of enormous size in order to see all the outside. With a model of ordinary size, some parts of the "outside" could only be explored by a crawling insect).

(v) We exclude from consideration cases where the parts can be divided into two sets, each giving a solid with as much symmetry as the whole figure. But we allow the combination of an enantiomorphous pair having no common part (which actually occurs in just one case).^[7]

Rules (i) to (iii) are symmetry requirements for the face planes. Rule (iv) excludes buried holes, to ensure that no two stellations look outwardly identical. Rule (v) prevents any disconnected compound of simpler stellations.

Coxeter

Coxeter was the main driving force behind the work. He carried out the original analysis based on Miller's rules, adopting a number of techniques such as combinatorics and abstract graph theory whose use in a geometrical context was then novel.

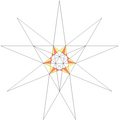
He observed that the stellation diagram comprised many line segments. He then developed procedures for manipulating combinations of the adjacent plane regions, to formally enumerate the combinations allowed under Miller's rules.

His graph, reproduced here, shows the connectivity of the various faces identified in the stellation diagram (see below). The Greek symbols represent sets of possible alternatives:

λ may be 3 or 4

μ may be 7 or 8

ν may be 11 or 12

Du Val

Du Val devised a symbolic notation for identifying sets of congruent cells, based on the observation that all the extended face (or boundary) planes together cut the space around the icosahedron in many different finite three dimensional regions that he called cells.

A segment between a point in a cell and the centre of the icosahedron intersects a number of (extended) face planes; this number is the power of the point and the cell. All cells with the same power form a shell (or layer). The inner icosahedron (power = 0) is named A, the shell with power 1 b, the shell with power 2 c, and so on. If all cells of a shell are congruent, they are named as the shell itself; if there are different non-congruent cells in a shell, they are numbered like e1 and e2. If an enantiomorphic pair of cells is in a shell, one of them is roman and the other italic like f1 and f1. (for example , there are 3 kinds of cells with power 5 (shell f): f1, f1 and f2.) Any combination of these cells form a stellated icosahedron, except that the last two of Millers conditions (see above) rule out certain combinations. A stellation consisting of a complete shell and all cells interior to it is named after the outer shell, capitalised, like B for A + b and De1 for A + b + c + d+ e1

With this scheme, Du Val tested all possible combinations against Miller's rules, confirming the result of Coxeter's approach.

Flather

Flather's contribution was indirect: he made card models of all 59. When he first met Coxeter he had already made many stellations, including some "non-Miller" examples. He went on to complete the series of fifty-nine, which are preserved in the mathematics library of Cambridge University, England. The library also holds some non-Miller models, but it is not known whether these were made by Flather or by Miller's later students.^[8]

Petrie

John Flinders Petrie was a lifelong friend of Coxeter and had a remarkable ability to visualise four-dimensional geometry. He and Coxeter had worked together on many mathematical problems. His direct contribution to the fifty-nine icosahedra was the exquisite set of three-dimensional drawings which provide much of the fascination of the published work.

The Crennells

For the Third Edition, Kate and David Crennell reset the text and redrew the diagrams. They also numbered the icosahedra, added a reference section containing tables, diagrams, and photographs of some of the Cambridge models (which at that time were all thought to be Flather's). Corrections to this edition have been published online.^[9]

Notes on the list

Cell diagram with Du Val notation for cells

Before Coxeter, only Brückner and Wheeler had recorded any significant sets of stellations, although a few such as the great icosahedron had been known for longer. Since publication of The 59, Wenninger published instructions on making models of many polyhedra, some being stellations of the icosahedra; the numbering scheme used in his book has become widely referenced, although he only recorded a few stellations of the icosahedra.

Index

• In the index numbering was added to the Third Edition by the Crennells, the first 32 icosahedra (indices 1–32) are reflective models, and the last 27 (indices 33–59) are chiral with only the right-handed forms listed. This index follows the order in which the stellations are depicted in the book (all editions).

Cells

• In Du Val's notation (see above) , each shell is identified in bold type, working outwards, as a, b, c, ..., h with a being the original icosahedron. Some shells subdivide into two types of cell, for example e comprises e₁ and e₂. The set f₁ further subdivides into right- and left-handed forms, respectively f₁ (plain type) and f₁ (italic). Where a stellation has all cells present within an outer shell, the outer shell is capitalised and the inner omitted, for example a + b + c + e₁ is written as Ce₁.

Stellation diagram with numbered face sets

Faces

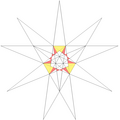
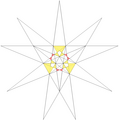
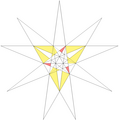
• All of the stellations can be specified by a stellation diagram. In the diagram shown here, the numbered colors indicate the regions of the stellation diagram which must occur together as a set, if full icosahedral symmetry is to be maintained. The diagram has 13 such sets. Some of these subdivide into chiral pairs (not shown), allowing stellations with rotational but not reflexive symmetry. In the table, faces which are seen from underneath (from the centre of the stellation) are indicated by an apostrophe, for example 3'.

Wenninger

• The index numbers and the numbered names were allocated arbitrarily by Wenninger's publisher according to their occurrence in his book Polyhedron models and bear no relation to any mathematical sequence. Only a few of his models were of icosahedra. His names are given in shortened form, with "... of the icosahedron" left off.

Wheeler

• The numbers and names of Wheeler's icosahedra (which by no means were intended to be a complete enumeration) are from the talk he gave as an Invited Speaker of the ICM in 1924 at Toronto.^[5]

Brückner

• Max Brückner made and photographed models of many polyhedra, only a few of which were icosahedra. Taf. is an abbreviation of Tafel, German for plate.

Remarks

• No. 8 is sometimes called the echidnahedron after an imagined similarity to the spiny anteater or echidna. This usage is independent of Kepler's description of his regular star polyhedra as his echidnae.

List of the fifty-nine icosahedra

Several more restrictive categories of stellated polyhedra have been identified, some are easily recognised:

• mainline stellations are the stellations whose name consist of a single capital letterA till (and including) H
• fully supported stellations: stellations where there are no overhangs, and all visible parts of a face can be seen from the same side. these are those stellations where in the faces column there is no face that has an apostrophe, for example 3'.

The only Kepler–Poinsot polyhedron in the list is the great icosahedron G.

The Great stellated dodecahedron is an edge-stellated icosahedron but only face-stellated icosahedra are in the list and it is therefore not included in the list.

Some images illustrate the mirror-image icosahedron with the f₁ rather than the f₁ cell.^[which?]

Index	Cells	Faces	Wenninger	Wheeler	Brückner	Remarks	Face diagram	3D
1	A	0	04 Icosahedron	1 Regular convex triangular		Regular icosahedron, a Platonic solid
2	B	1	26 Triakis icosahedron	2 Hexagonal	Taf. VIII, Fig. 2	First stellation of the icosahedron, small triambic icosahedron, or triakisicosahedron
3	C	2	23 Compound of five octahedra	3 Five intersecting octahedra	Taf. IX, Fig. 6	Regular compound of five octahedra
4	D	3 4	99	4 Nonagonal	Taf. IX, Fig. 17
5	E	5 6 7	99	99
6	F	8 9 10	27 Second stellation	19 triple 13+6+7		Second stellation of icosahedron
7	G	11 12	41 Great icosahedron	11 Regular star Poinsot	Taf. XI, Fig. 24	Great icosahedron
8	H	13	42 Final stellation	12 Complete	Taf. XI, Fig. 14	Final stellation of the icosahedron or echidnahedron
9	e1	3' 5	37 Twelfth stellation	99		Twelfth stellation of icosahedron
10	f1	5' 6' 9 10	99	99
11	g1	10' 12	29 Fourth stellation	21 Discrete skeleton		Fourth stellation of icosahedron
12	e1f1	3' 6' 9 10	99	99
13	e1f1g1	3' 6' 9 12	99	20 Hollow, labyrinth
14	f1g1	5' 6' 9 12	99	99
15	e2	4' 6 7	99	99
16	f2	7' 8	99	22 Discrete twelve-pointed, crown-rimmed group
17	g2	8' 9'11	99	99
18	e2f2	4' 6 8	99	99
19	e2f2g2	4' 6 9' 11	99	99
20	f2g2	7' 9' 11	30 Fifth stellation	99		Fifth stellation of icosahedron
21	De1	4 5	32 Seventh stellation	10 Twenty-pointed, six-edged		Seventh stellation of icosahedron
22	Ef1	7 9 10	25 Compound of ten tetrahedra	8 Ten intersecting tetrahedra	Taf. IX, Fig. 3	Regular compound of ten tetrahedra
23	Fg1	8 9 12	31 Sixth stellation	17 Double 13+ 9	Taf. X, Fig. 3	Sixth stellation of icosahedron
24	De1f1	4 6' 9 10	99	99
25	De1f1g1	4 6' 9 12	99	99
26	Ef1g1	7 9 12	28 Third stellation	9 Mobius (concave)	Taf. VIII, Fig. 26	Excavated dodecahedron
27	De2	3 6 7	99	5 Archimedian variety of no 13
28	Ef2	5 6 8	99	18 Double 13 + 10	Taf.IX, Fig. 20
29	Fg2	10 11	33 Eighth stellation	14 Archimedian variety 11		Eighth stellation of icosahedron
30	De2f2	3 6 8	34 Ninth stellation	13 Kite archimedian variety no 11		Medial triambic icosahedron or Great triambic icosahedron
31	De2f2g2	3 6 9' 11	99	99
32	Ef2g2	5 6 9' 11	99	99
33	f1	5' 6' 9 10	35 Tenth stellation	99		Tenth stellation of icosahedron
34	e1f1	3' 5 6' 9 10	36 Eleventh stellation	99		Eleventh stellation of icosahedron
35	De1f1	4 5 6' 9 10	99	99
36	f1g1	5' 6' 9 10' 12	99	99
37	e1f1g1	3' 5 6' 9 10' 12	39 Fourteenth stellation	99		Fourteenth stellation of icosahedron
38	De1f1g1	4 5 6' 9 10' 12	99	99
39	f1g2	5' 6' 8' 9' 10 11	99	99
40	e1f1g2	3' 5 6' 8' 9' 10 11	99	99
41	De1f1g2	4 5 6' 8' 9' 10 11	99	99
42	f1f2g2	5' 6' 7' 9' 10 11	99	99
43	e1f1f2g2	3' 5 6' 7' 9' 10 11	99	99
44	De1f1f2g2	4 5 6' 7' 9' 10 11	99	99
45	e2f1	4' 5' 6 7 9 10	40 Fifteenth stellation	99		Fifteenth stellation of icosahedron
46	De2f1	3 5' 6 7 9 10	99	99
47	Ef1	5 6 7 9 10	24 Compound of five tetrahedra	7: right handed 6: left handed Five intersecting Tetrahedra	Taf. IX, Fig. 11	Regular Compound of five tetrahedra (right handed)
48	e2f1g1	4' 5' 6 7 9 10' 12	99	99
49	De2f1g1	3 5' 6 7 9 10' 12	99	99
50	Ef1g1	5 6 7 9 10' 12	99	99
51	e2f1f2	4' 5' 6 8 9 10	38 Thirteenth stellation	99		Thirteenth stellation of icosahedron
52	De2f1f2	3 5' 6 8 9 10	99	99
53	Ef1f2	5 6 8 9 10	99	15: right handed 16: left handed Double 13+7
54	e2f1f2g1	4' 5' 6 8 9 10' 12	99	99
55	De2f1f2g1	3 5' 6 8 9 10' 12	99	99
56	Ef1f2g1	5 6 8 9 10' 12	99	99
57	e2f1f2g2	4' 5' 6 9' 10 11	99	99
58	De2f1f2g2	3 5' 6 9' 10 11	99	99
59	Ef1f2g2	5 6 9' 10 11	99	99

Subsequent debate

There has subsequently been some debate on Miller's rules, with some writers questioning them. Flather himself made and exhibited models which were "non-Miller".^[10] Bridge (1974) obtained stellations of the icosahedron by dualising facettings of the dodecahedron, noting the significance of internal structure in distinguishing between stellations which Miller's rules treat as identical.^[11] Hudson and Kingston (1988) adopted a reduced rule set.^[12] Inchbald noted two non-Miller stellations, and went on to discuss various related issues.^[13][14]

See also

• List of Wenninger polyhedron models – Wenninger's book Polyhedron models included 21 of these stellations.
• Solids with icosahedral symmetry