Top Qs
Timeline
Chat
Perspective
Torque
Turning force around an axis From Wikipedia, the free encyclopedia
Remove ads
In physics and mechanics, torque is the rotational correspondent of linear force.[1] It is also referred to as the moment of force, or simply the moment. Just as a linear force is a push or a pull applied to a body, a torque can be thought of as a twist applied to an object with respect to a chosen axis; for example, driving a screw uses torque to force it into an object, which is applied by the screwdriver rotating around its axis to the drives on the head.
Torque is generally referred to using different vocabulary depending on geographical location and field of study, with torque generally being associated with physics and moment being associated with engineering. This article follows the definition used in US physics in its usage of the word torque.[2]
Torque is typically represented mathematically using the lowercase Greek letter tau (). When being referred to as moment of force, it is commonly denoted by M.
Remove ads
Historical terminology
The term torque (from Latin torquēre, 'to twist') is said to have been suggested by James Thomson and appeared in print in April, 1884.[3][4][5] Usage is attested the same year by Silvanus P. Thompson in the first edition of Dynamo-Electric Machinery.[5] Thompson describes his usage of the term as follows:[4]
Just as the Newtonian definition of force is that which produces or tends to produce motion (along a line), so torque may be defined as that which produces or tends to produce torsion (around an axis). It is better to use a term which treats this action as a single definite entity than to use terms like "couple" and "moment", which suggest more complex ideas. The single notion of a twist applied to turn a shaft is better than the more complex notion of applying a linear force (or a pair of forces) with a certain leverage.
In mechanical engineering in the UK and the US, torque is generally referred to as moment of force, usually shortened to moment.[6] This terminology can be traced back to at least 1811 in Siméon Denis Poisson's Traité de mécanique.[7] An English translation of Poisson's work appeared in 1842.
Remove ads
Definition and relation to other physical quantities
Summarize
Perspective
Torque as a Cross Product Between Linear Force and the Radius about the Rotational Axis

The torque about an axis can be calculated by multiplying the linear force applied perpendicularly to a lever multiplied by its distance from the lever's fulcrum (the length of the lever arm).
Therefore, torque is defined as the product of the magnitude of the perpendicular component of the force and the distance of the line of action of a force from the point around which it is being determined.
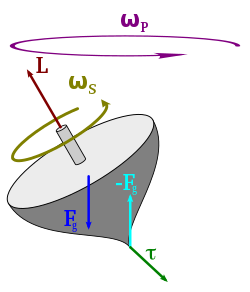
In three dimensions, the torque is a pseudovector; for point particles, it is given by the cross product of the displacement vector and the force vector. The direction of the torque can be determined by using the right-hand grip rule: if the fingers of the right hand are curled from the direction of the lever arm to the direction of the force, then the thumb points in the direction of the torque.[8] It follows that the torque vector is perpendicular to both the position and force vectors, and defines the plane in which the two vectors lie. The resulting torque vector direction is determined by the right-hand rule. Therefore any force directed parallel to the particle's position vector does not produce a torque.[9][10] The magnitude of torque applied to a rigid body depends on three quantities: the force applied, the lever arm vector[11] connecting the point about which the torque is being measured to the point of force application, and the angle between the force and lever arm vectors. In symbols:
where
- is the torque vector and is the magnitude of the torque;
- is the position vector (a vector from the point about which the torque is being measured to the point where the force is applied), and r is the magnitude of the position vector;
- is the force vector, F is the magnitude of the force vector, and F⊥ is the amount of force directed perpendicularly to the position of the particle;
- denotes the cross product, which produces a vector that is perpendicular both to r and to F following the right-hand rule;
- is the angle between the force vector and the lever arm vector.
The SI unit for torque is the newton-meter (N⋅m). For more on the units of torque, see § Units.
Relationship with the angular momentum
The net torque on a body determines the rate of change of the body's angular momentum,
where is the angular momentum vector and is time. For the motion of a point particle,
where is the moment of inertia and is the orbital angular velocity pseudovector. It follows that
using the derivative of a vector is This equation is the rotational analogue of Newton's second law for point particles, and is valid for any type of trajectory. In some simple cases like a rotating disc, where only the moment of inertia on rotating axis is, the rotational Newton's second law can bewhere .
Proof of the equivalence of definitions
The definition of angular momentum for a single point particle is: where p is the particle's linear momentum and r is the position vector from the origin. The time-derivative of this is:
This result can easily be proven by splitting the vectors into components and applying the product rule. But because the rate of change of linear momentum is force and the rate of change of position is velocity ,
The cross product of momentum with its associated velocity is zero because velocity and momentum are parallel, so the second term vanishes. Therefore, torque on a particle is equal to the first derivative of its angular momentum with respect to time. If multiple forces are applied, according Newton's second law it follows that
This is a general proof for point particles, but it can be generalized to a system of point particles by applying the above proof to each of the point particles and then summing over all the point particles. Similarly, the proof can be generalized to a continuous mass by applying the above proof to each point within the mass, and then integrating over the entire mass.
Derivatives of torque
In physics, rotatum is the derivative of torque with respect to time[12]
where τ is torque.
This word is derived from the Latin word rotātus meaning 'to rotate'. The term rotatum is not universally recognized but is commonly used. There is not a universally accepted lexicon to indicate the successive derivatives of rotatum, even if sometimes various proposals have been made.
Using the cross product definition of torque, an alternative expression for rotatum is:
Because the rate of change of force is yank and the rate of change of position is velocity , the expression can be further simplified to:
Relationship with power and energy
The law of conservation of energy can also be used to understand torque. If a force is allowed to act through a distance, it is doing mechanical work. Similarly, if torque is allowed to act through an angular displacement, it is doing work. Mathematically, for rotation about a fixed axis through the center of mass, the work W can be expressed as
where τ is torque, and θ1 and θ2 represent (respectively) the initial and final angular positions of the body.[13]
It follows from the work–energy principle that W also represents the change in the rotational kinetic energy Er of the body, given by
where I is the moment of inertia of the body and ω is its angular speed.[13]
Power is the work per unit time, given by
where P is power, τ is torque, ω is the angular velocity, and represents the scalar product.
Algebraically, the equation may be rearranged to compute torque for a given angular speed and power output. The power injected by the torque depends only on the instantaneous angular speed – not on whether the angular speed increases, decreases, or remains constant while the torque is being applied (this is equivalent to the linear case where the power injected by a force depends only on the instantaneous speed – not on the resulting acceleration, if any).
Proof
The work done by a variable force acting over a finite linear displacement is given by integrating the force with respect to an elemental linear displacement
However, the infinitesimal linear displacement is related to a corresponding angular displacement and the radius vector as
Substitution in the above expression for work, , gives
The expression inside the integral is a scalar triple product , but as per the definition of torque, and since the parameter of integration has been changed from linear displacement to angular displacement, the equation becomes
If the torque and the angular displacement are in the same direction, then the scalar product reduces to a product of magnitudes; i.e., giving
Remove ads
Principle of moments
Summarize
Perspective
The principle of moments, also known as Varignon's theorem (not to be confused with the geometrical theorem of the same name) states that the resultant torques due to several forces applied to about a point is equal to the sum of the contributing torques:
From this it follows that the torques resulting from N number of forces acting around a pivot on an object are balanced when
Remove ads
Units
Summarize
Perspective
Official SI literature indicates the newton-meter as the standard unit for torque, properly denoted using N⋅m; although this is dimensionally equivalent to the joule, which is not used for torque.[14][15] In the case of torque, the unit is assigned to a vector, whereas for energy, it is assigned to a scalar. This means that the dimensional equivalence of the newton-metre and the joule may be applied in the former but not in the latter case. This problem is addressed in orientational analysis, which treats the radian as a base unit rather than as a dimensionless unit.[16] Torque has the dimension of force times distance, symbolically T−2L2M, and those fundamental dimensions are the same as that for energy or work.
The traditional imperial units for torque are the pound foot (lbf-ft), or, for small values, the pound inch (lbf-in). In the US, torque is most commonly referred to as the foot-pound (denoted as either lb-ft or ft-lb) and the inch-pound (denoted as in-lb).[17][18] Practitioners depend on context and the hyphen in the abbreviation to know that these refer to torque and not to energy or moment of mass (as the symbolism ft-lb would properly imply).
Conversion to other units
A conversion factor may be necessary when using different units of power or torque. For example, if rotational speed (unit: revolution per minute or second) is used in place of angular speed (unit: radian per second), we must multiply by 2π radians per revolution. In the following formulas, P is power, τ is torque, and ν (Greek letter nu) is rotational speed.
Showing units:
Dividing by 60 seconds per minute gives us the following.
where rotational speed is in revolutions per minute (rpm, rev/min).
Some people (e.g., American automotive engineers) use horsepower (mechanical) for power, foot-pounds (lbf⋅ft) for torque and rpm for rotational speed. This results in the formula changing to:
The constant below (in foot-pounds per minute) changes with the definition of the horsepower; for example, using metric horsepower, it becomes approximately 32,550.
The use of other units (e.g., BTU per hour for power) would require a different custom conversion factor.
Derivation
For a rotating object, the linear distance covered at the circumference of rotation is the product of the radius with the angle covered. That is: linear distance = radius × angular distance. And by definition, linear distance = linear speed × time = radius × angular speed × time.
By the definition of torque: torque = radius × force. We can rearrange this to determine force = torque ÷ radius. These two values can be substituted into the definition of power:
The radius r and time t have dropped out of the equation. However, angular speed must be in radians per unit of time, by the assumed direct relationship between linear speed and angular speed at the beginning of the derivation. If the rotational speed is measured in revolutions per unit of time, the linear speed and distance are increased proportionately by 2π in the above derivation to give:
If torque is in newton-metres and rotational speed in revolutions per second, the above equation gives power in newton-metres per second or watts. If Imperial units are used, and if torque is in pounds-force feet and rotational speed in revolutions per minute, the above equation gives power in foot pounds-force per minute. The horsepower form of the equation is then derived by applying the conversion factor 33,000 ft⋅lbf/min per horsepower:
because
Remove ads
Special cases and other facts
Summarize
Perspective
Moment arm formula

A very useful special case, often given as the definition of torque in fields other than physics, is as follows:
The construction of the "moment arm" is shown in the figure to the right, along with the vectors r and F mentioned above. The problem with this definition is that it does not give the direction of the torque but only the magnitude, and hence it is difficult to use in three-dimensional cases. If the force is perpendicular to the displacement vector r, the moment arm will be equal to the distance to the centre, and torque will be a maximum for the given force. The equation for the magnitude of a torque, arising from a perpendicular force:
For example, if a person places a force of 10 N at the terminal end of a wrench that is 0.5 m long (or a force of 10 N acting 0.5 m from the twist point of a wrench of any length), the torque will be 5 N⋅m – assuming that the person moves the wrench by applying force in the plane of movement and perpendicular to the wrench.
Static equilibrium
For an object to be in static equilibrium, not only must the sum of the forces be zero, but also the sum of the torques (moments) about any point. For a two-dimensional situation with horizontal and vertical forces, the sum of the forces requirement is two equations: ΣH = 0 and ΣV = 0, and the torque a third equation: Στ = 0. That is, to solve statically determinate equilibrium problems in two-dimensions, three equations are used.
Net force versus torque
When the net force on the system is zero, the torque measured from any point in space is the same. For example, the torque on a current-carrying loop in a uniform magnetic field is the same regardless of the point of reference. If the net force is not zero, and is the torque measured from , then the torque measured from is
Machine torque

Torque forms part of the basic specification of an engine: the power output of an engine is expressed as its torque multiplied by the angular speed of the drive shaft. Internal-combustion engines produce useful torque only over a limited range of rotational speeds (typically from around 1,000–6,000 rpm for a small car). One can measure the varying torque output over that range with a dynamometer, and show it as a torque curve. Steam engines and electric motors tend to produce maximum torque close to zero rpm, with the torque diminishing as rotational speed rises (due to increasing friction and other constraints). Reciprocating steam-engines and electric motors can start heavy loads from zero rpm without a clutch.
In practice, the relationship between power and torque can be observed in bicycles: Bicycles are typically composed of two road wheels, front and rear gears (referred to as sprockets) meshing with a chain, and a derailleur mechanism if the bicycle's transmission system allows multiple gear ratios to be used (i.e. multi-speed bicycle), all of which attached to the frame. A cyclist, the person who rides the bicycle, provides the input power by turning pedals, thereby cranking the front sprocket (commonly referred to as chainring). The input power provided by the cyclist is equal to the product of angular speed (i.e. the number of pedal revolutions per minute times 2π) and the torque at the spindle of the bicycle's crankset. The bicycle's drivetrain transmits the input power to the road wheel, which in turn conveys the received power to the road as the output power of the bicycle. Depending on the gear ratio of the bicycle, a (torque, angular speed)input pair is converted to a (torque, angular speed)output pair. By using a larger rear gear, or by switching to a lower gear in multi-speed bicycles, angular speed of the road wheels is decreased while the torque is increased, product of which (i.e. power) does not change.
Torque multiplier
Torque can be multiplied via three methods: by locating the fulcrum such that the length of a lever is increased; by using a longer lever; or by the use of a speed-reducing gearset or gear box. Such a mechanism multiplies torque, as rotation rate is reduced.
Remove ads
See also
References
External links
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads




















































![{\displaystyle {\begin{aligned}{\text{power}}&={\frac {{\text{force}}\cdot {\text{linear distance}}}{\text{time}}}\\[6pt]&={\frac {\left({\dfrac {\text{torque}}{r}}\right)\cdot (r\cdot {\text{angular speed}}\cdot t)}{t}}\\[6pt]&={\text{torque}}\cdot {\text{angular speed}}.\end{aligned}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/4382d186e4085de735546ad46847d852af843fcb)

![{\displaystyle {\begin{aligned}{\text{power}}&={\text{torque}}\cdot 2\pi \cdot {\text{rotational speed}}\cdot {\frac {{\text{ft}}{\cdot }{\text{lbf}}}{\text{min}}}\cdot {\frac {\text{horsepower}}{33,\!000\cdot {\frac {{\text{ft}}\cdot {\text{lbf}}}{\text{min}}}}}\\[6pt]&\approx {\frac {{\text{torque}}\cdot {\text{RPM}}}{5,\!252}}\end{aligned}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/db904e5528e26299e0a8926baf3b676956337dfc)






