10-orthoplex

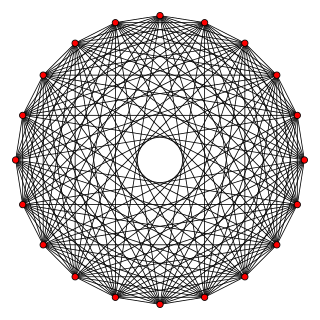
In geometry, a 10-orthoplex or 10-cross polytope, is a regular 10-polytope with 20 vertices, 180 edges, 960 triangle faces, 3360 tetrahedron cells, 8064 5-cell 4-faces, 13440 5-faces, 15360 6-faces, 11520 7-faces, 5120 8-faces, and 1024 9-faces.

10-orthoplex Decacross
Orthogonal projection inside Petrie polygon
Type	Regular 10-polytope
Family	Orthoplex
Schläfli symbol	{38,4} {37,31,1}
Coxeter-Dynkin diagrams
9-faces	1024 {38}
8-faces	5120 {37}
7-faces	11520 {36}
6-faces	15360 {35}
5-faces	13440 {34}
4-faces	8064 {33}
Cells	3360 {3,3}
Faces	960 {3}
Edges	180
Vertices	20 ⋅
Vertex figure	9-orthoplex
Petrie polygon	Icosagon
Coxeter groups	C10, [38,4] D10, [37,1,1]
Dual	10-cube
Properties	Convex, Hanner polytope

It has two constructed forms, the first being regular with Schläfli symbol {3⁸,4}, and the second with alternately labeled (checker-boarded) facets, with Schläfli symbol {3⁷,3^1,1} or Coxeter symbol 7₁₁.

It is one of an infinite family of polytopes, called cross-polytopes or orthoplexes. The dual polytope is the 10-hypercube or 10-cube.

Alternate names

• Decacross is derived from combining the family name cross polytope with deca for ten (dimensions) in Greek. Acronym: ka^[1]
• Chilliaicositetraronnon as a 1024-facetted 10-polytope (polyronnon).^[2]

Construction

There are two Coxeter groups associated with the 10-orthoplex, one regular, dual of the 10-cube with the C₁₀ or [4,3⁸] symmetry group, and a lower symmetry with two copies of 9-simplex facets, alternating, with the D₁₀ or [3^7,1,1] symmetry group.

Cartesian coordinates

Cartesian coordinates for the vertices of a 10-orthoplex, centred at the origin are

(±1,0,0,0,0,0,0,0,0,0), (0,±1,0,0,0,0,0,0,0,0), (0,0,±1,0,0,0,0,0,0,0), (0,0,0,±1,0,0,0,0,0,0), (0,0,0,0,±1,0,0,0,0,0), (0,0,0,0,0,±1,0,0,0,0), (0,0,0,0,0,0,±1,0,0,0), (0,0,0,0,0,0,0,±1,0,0), (0,0,0,0,0,0,0,0,±1,0), (0,0,0,0,0,0,0,0,0,±1)

Every vertex pair is connected by an edge, except opposites.

Images

Orthographic projections

B10	B9	B8
[20]	[18]	[16]
B7	B6	B5
[14]	[12]	[10]
B4	B3	B2
[8]	[6]	[4]
A9		A5
—		—
[10]		[6]
A7		A3
—		—
[8]		[4]