6-polytope

In six-dimensional geometry, a six-dimensional polytope or 6-polytope is a polytope, bounded by 5-polytope facets.

Graphs of three regular and five Uniform 6-polytopes

6-simplex	6-orthoplex, 311	6-cube (Hexeract)	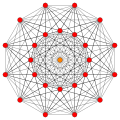221
Expanded 6-simplex	Rectified 6-orthoplex	6-demicube 131 (Demihexeract)	122

Definition

A 6-polytope is a closed six-dimensional figure with vertices, edges, faces, cells (3-faces), 4-faces, and 5-faces. A vertex is a point where six or more edges meet. An edge is a line segment where four or more faces meet, and a face is a polygon where three or more cells meet. A cell is a polyhedron. A 4-face is a polychoron, and a 5-face is a 5-polytope. Furthermore, the following requirements must be met:

• Each 4-face must join exactly two 5-faces (facets).
• Adjacent facets are not in the same five-dimensional hyperplane.
• The figure is not a compound of other figures which meet the requirements.

Characteristics

The topology of any given 6-polytope is defined by its Betti numbers and torsion coefficients.^[1]

The value of the Euler characteristic used to characterise polyhedra does not generalize usefully to higher dimensions, and is zero for all 6-polytopes, whatever their underlying topology. This inadequacy of the Euler characteristic to reliably distinguish between different topologies in higher dimensions led to the discovery of the more sophisticated Betti numbers.^[1]

Similarly, the notion of orientability of a polyhedron is insufficient to characterise the surface twistings of toroidal polytopes, and this led to the use of torsion coefficients.^[1]

Classification

6-polytopes may be classified by properties like "convexity" and "symmetry".

• A 6-polytope is convex if its boundary (including its 5-faces, 4-faces, cells, faces and edges) does not intersect itself and the line segment joining any two points of the 6-polytope is contained in the 6-polytope or its interior; otherwise, it is non-convex. Self-intersecting 6-polytope are also known as star 6-polytopes, from analogy with the star-like shapes of the non-convex Kepler-Poinsot polyhedra.
• A regular 6-polytope has all identical regular 5-polytope facets. All regular 6-polytope are convex.

Main article: List of regular polytopes § Convex_5

• A semi-regular 6-polytope contains two or more types of regular 4-polytope facets. There is only one such figure, called 2₂₁.
• A uniform 6-polytope has a symmetry group under which all vertices are equivalent, and its facets are uniform 5-polytopes. The faces of a uniform polytope must be regular.

Main article: Uniform 6-polytope

• A prismatic 6-polytope is constructed by the Cartesian product of two lower-dimensional polytopes. A prismatic 6-polytope is uniform if its factors are uniform. The 6-cube is prismatic (product of a squares and a cube), but is considered separately because it has symmetries other than those inherited from its factors.
• A 5-space tessellation is the division of five-dimensional Euclidean space into a regular grid of 5-polytope facets. Strictly speaking, tessellations are not 6-polytopes as they do not bound a "6D" volume, but we include them here for the sake of completeness because they are similar in many ways to 6-polytope. A uniform 5-space tessellation is one whose vertices are related by a space group and whose facets are uniform 5-polytopes.

Regular 6-polytopes

Regular 6-polytopes can be generated from Coxeter groups represented by the Schläfli symbol {p,q,r,s,t} with t {p,q,r,s} 5-polytope facets around each cell.

There are only three such convex regular 6-polytopes:

• {3,3,3,3,3} - 6-simplex
• {4,3,3,3,3} - 6-cube
• {3,3,3,3,4} - 6-orthoplex

There are no nonconvex regular polytopes of 5 or more dimensions.

For the three convex regular 6-polytopes, their elements are:

Name	Schläfli symbol	Coxeter diagram	Vertices	Edges	Faces	Cells	4-faces	5-faces	Symmetry (order)
6-simplex	{3,3,3,3,3}		7	21	35	35	21	7	A6 (720)
6-orthoplex	{3,3,3,3,4}		12	60	160	240	192	64	B6 (46080)
6-cube	{4,3,3,3,3}		64	192	240	160	60	12	B6 (46080)

Uniform 6-polytopes

Main article: Uniform 6-polytope

Here are six simple uniform convex 6-polytopes, including the 6-orthoplex repeated with its alternate construction.

Name	Schläfli symbol(s)	Coxeter diagram(s)	Vertices	Edges	Faces	Cells	4-faces	5-faces	Symmetry (order)
Expanded 6-simplex	t0,5{3,3,3,3,3}		42	210	490	630	434	126	2×A6 (1440)
6-orthoplex, 311 (alternate construction)	{3,3,3,31,1}		12	60	160	240	192	64	D6 (23040)
6-demicube	{3,33,1} h{4,3,3,3,3}		32	240	640	640	252	44	D6 (23040) ½B6
Rectified 6-orthoplex	t1{3,3,3,3,4} t1{3,3,3,31,1}		60	480	1120	1200	576	76	B6 (46080) 2×D6
221 polytope	{3,3,32,1}		27	216	720	1080	648	99	E6 (51840)
122 polytope	{3,32,2}	or	72	720	2160	2160	702	54	2×E6 (103680)

The expanded 6-simplex is the vertex figure of the uniform 6-simplex honeycomb, . The 6-demicube honeycomb, , vertex figure is a rectified 6-orthoplex and facets are the 6-orthoplex and 6-demicube. The uniform 2₂₂ honeycomb,, has 1₂₂ polytope is the vertex figure and 2₂₁ facets.