6-cube

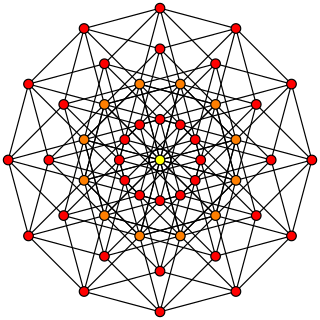
In geometry, a 6-cube is a six-dimensional hypercube with 64 vertices, 192 edges, 240 square faces, 160 cubic cells, 60 tesseract 4-faces, and 12 5-cube 5-faces.

6-cube Hexeract
Orthogonal projection inside Petrie polygon Orange vertices are doubled, and the center yellow has 4 vertices
Type	Regular 6-polytope
Family	hypercube
Schläfli symbol	{4,34}
Coxeter diagram
5-faces	12 {4,3,3,3}
4-faces	60 {4,3,3}
Cells	160 {4,3}
Faces	240 {4}
Edges	192
Vertices	64
Vertex figure	5-simplex
Petrie polygon	dodecagon
Coxeter group	B6, [34,4]
Dual	6-orthoplex
Properties	convex, Hanner polytope

It has Schläfli symbol {4,3⁴}, being composed of 3 5-cubes around each 4-face. It can be called a hexeract, a portmanteau of tesseract (the 4-cube) with hex for six (dimensions) in Greek. It can also be called a regular dodeca-6-tope or dodecapeton, being a 6-dimensional polytope constructed from 12 regular facets.

Related polytopes

It is a part of an infinite family of polytopes, called hypercubes. The dual of a 6-cube can be called a 6-orthoplex, and is a part of the infinite family of cross-polytopes. It is composed of various 5-cubes, at perpendicular angles on the u-axis, forming coordinates (x,y,z,w,v,u).^[1][2]

Applying an alternation operation, deleting alternating vertices of the 6-cube, creates another uniform polytope, called a 6-demicube, (part of an infinite family called demihypercubes), which has 12 5-demicube and 32 5-simplex facets.

As a configuration

This configuration matrix represents the 6-cube. The rows and columns correspond to vertices, edges, faces, cells, 4-faces and 5-faces. The diagonal numbers say how many of each element occur in the whole 6-cube. The nondiagonal numbers say how many of the column's element occur in or at the row's element.^[3][4]

${\displaystyle {\begin{bmatrix}{\begin{matrix}64&6&15&20&15&6\\2&192&5&10&10&5\\4&4&240&4&6&4\\8&12&6&160&3&3\\16&32&24&8&60&2\\32&80&80&40&10&12\end{matrix}}\end{bmatrix}}}$

Cartesian coordinates

Cartesian coordinates for the vertices of a 6-cube centered at the origin and edge length 2 are

(±1,±1,±1,±1,±1,±1)

while the interior of the same consists of all points (x₀, x₁, x₂, x₃, x₄, x₅) with −1 < x_i < 1.

Construction

There are three Coxeter groups associated with the 6-cube, one regular, with the C₆ or [4,3,3,3,3] Coxeter group, and a half symmetry (D₆) or [3^3,1,1] Coxeter group. The lowest symmetry construction is based on hyperrectangles or proprisms, cartesian products of lower dimensional hypercubes.

Name	Coxeter	Schläfli	Symmetry	Order
Regular 6-cube		{4,3,3,3,3}	[4,3,3,3,3]	46080
Quasiregular 6-cube			[3,3,3,31,1]	23040
hyperrectangle		{4,3,3,3}×{}	[4,3,3,3,2]	7680
		{4,3,3}×{4}	[4,3,3,2,4]	3072
		{4,3}2	[4,3,2,4,3]	2304
		{4,3,3}×{}2	[4,3,3,2,2]	1536
		{4,3}×{4}×{}	[4,3,2,4,2]	768
		{4}3	[4,2,4,2,4]	512
		{4,3}×{}3	[4,3,2,2,2]	384
		{4}2×{}2	[4,2,4,2,2]	256
		{4}×{}4	[4,2,2,2,2]	128
		{}6	[2,2,2,2,2]	64

Projections

orthographic projections

Coxeter plane	B6	B5	B4
Graph
Dihedral symmetry	[12]	[10]	[8]
Coxeter plane	Other	B3	B2
Graph
Dihedral symmetry	[2]	[6]	[4]
Coxeter plane		A5	A3
Graph
Dihedral symmetry		[6]	[4]

3D Projections
6-cube 6D simple rotation through 2Pi with 6D perspective projection to 3D.	6-cube quasicrystal structure orthographically projected to 3D using the golden ratio.
A 3D perspective projection of a hexeract undergoing a triple rotation about the X-W1, Y-W2 and Z-W3 orthogonal planes.

Related polytopes

The 64 vertices of a 6-cube also represent a regular skew 4-polytope {4,3,4 | 4}. Its net can be seen as a 4×4×4 matrix of 64 cubes, a periodic subset of the cubic honeycomb, {4,3,4}, in 3-dimensions. It has 192 edges, and 192 square faces. Opposite faces fold together into a 4-cycle. Each fold direction adds 1 dimension, raising it into 6-space.

The 6-cube is 6th in a series of hypercube:

Petrie polygon orthographic projections

Line segment	Square	Cube	4-cube	5-cube	6-cube	7-cube	8-cube	9-cube	10-cube

This polytope is one of 63 uniform 6-polytopes generated from the B₆ Coxeter plane, including the regular 6-cube or 6-orthoplex.

B6 polytopes
β6	t1β6	t2β6	t2γ6	t1γ6	γ6	t0,1β6	t0,2β6
t1,2β6	t0,3β6	t1,3β6	t2,3γ6	t0,4β6	t1,4γ6	t1,3γ6	t1,2γ6
t0,5γ6	t0,4γ6	t0,3γ6	t0,2γ6	t0,1γ6	t0,1,2β6	t0,1,3β6	t0,2,3β6
t1,2,3β6	t0,1,4β6	t0,2,4β6	t1,2,4β6	t0,3,4β6	t1,2,4γ6	t1,2,3γ6	t0,1,5β6
t0,2,5β6	t0,3,4γ6	t0,2,5γ6	t0,2,4γ6	t0,2,3γ6	t0,1,5γ6	t0,1,4γ6	t0,1,3γ6
t0,1,2γ6	t0,1,2,3β6	t0,1,2,4β6	t0,1,3,4β6	t0,2,3,4β6	t1,2,3,4γ6	t0,1,2,5β6	t0,1,3,5β6
t0,2,3,5γ6	t0,2,3,4γ6	t0,1,4,5γ6	t0,1,3,5γ6	t0,1,3,4γ6	t0,1,2,5γ6	t0,1,2,4γ6	t0,1,2,3γ6
t0,1,2,3,4β6	t0,1,2,3,5β6	t0,1,2,4,5β6	t0,1,2,4,5γ6	t0,1,2,3,5γ6	t0,1,2,3,4γ6	t0,1,2,3,4,5γ6