Arcsine distribution

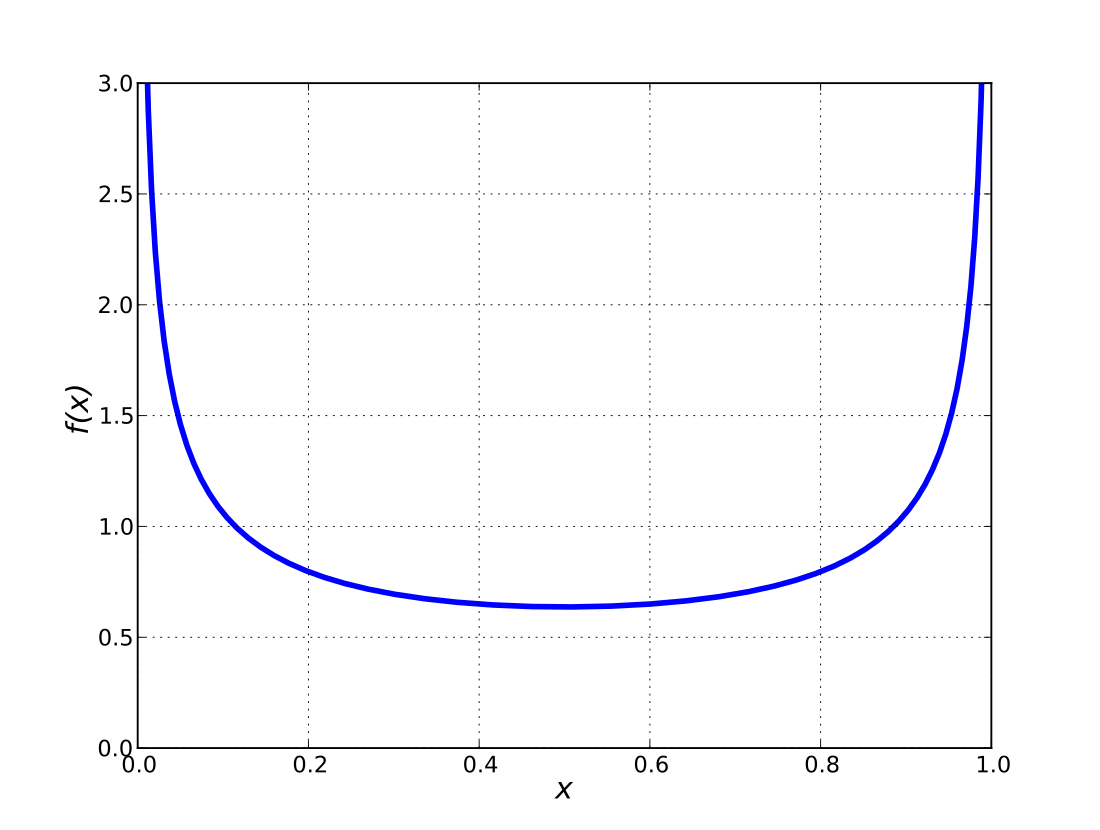
In probability theory, the arcsine distribution is the probability distribution whose cumulative distribution function involves the arcsine and the square root:

${\displaystyle F(x)={\frac {2}{\pi }}\arcsin \left({\sqrt {x}}\right)={\frac {\arcsin(2x-1)}{\pi }}+{\frac {1}{2}}}$

Arcsine

Probability density function
Cumulative distribution function
Parameters	none
Support	${\displaystyle x\in (0,1)}$
PDF	${\displaystyle f(x)={\frac {1}{\pi {\sqrt {x(1-x)}}}}}$
CDF	${\displaystyle F(x)={\frac {2}{\pi }}\arcsin \left({\sqrt {x}}\right)}$
Mean	${\displaystyle {\frac {1}{2}}}$
Median	${\displaystyle {\frac {1}{2}}}$
Mode	${\displaystyle x\in \{0,1\}}$
Variance	${\displaystyle {\tfrac {1}{8}}}$
Skewness	${\displaystyle 0}$
Excess kurtosis	${\displaystyle -{\tfrac {3}{2}}}$
Entropy	${\displaystyle \ln {\tfrac {\pi }{4}}}$
MGF	${\displaystyle 1+\sum _{k=1}^{\infty }\left(\prod _{r=0}^{k-1}{\frac {2r+1}{2r+2}}\right){\frac {t^{k}}{k!}}}$
CF	${\displaystyle e^{i{\frac {t}{2}}}J_{0}({\frac {t}{2}})}$

for 0 ≤ x ≤ 1, and whose probability density function is

${\displaystyle f(x)={\frac {1}{\pi {\sqrt {x(1-x)}}}}}$

on (0, 1). The standard arcsine distribution is a special case of the beta distribution with α = β = 1/2. That is, if ${\displaystyle X}$ is an arcsine-distributed random variable, then ${\displaystyle X\sim {\rm {Beta}}{\bigl (}{\tfrac {1}{2}},{\tfrac {1}{2}}{\bigr )}}$. By extension, the arcsine distribution is a special case of the Pearson type I distribution.

The arcsine distribution appears in the Lévy arcsine law, in the Erdős arcsine law, and as the Jeffreys prior for the probability of success of a Bernoulli trial.^[1][2] The arcsine probability density is a distribution that appears in several random-walk fundamental theorems. In a fair coin toss random walk, the probability for the time of the last visit to the origin is distributed as an (U-shaped) arcsine distribution.^[3][4] In a two-player fair-coin-toss game, a player is said to be in the lead if the random walk (that started at the origin) is above the origin. The most probable number of times that a given player will be in the lead, in a game of length 2N, is not N. On the contrary, N is the least likely number of times that the player will be in the lead. The most likely number of times in the lead is 0 or 2N (following the arcsine distribution).

Generalization

Arcsine – bounded support

Parameters	${\displaystyle -\infty <a<b<\infty \,}$
Support	${\displaystyle x\in (a,b)}$
PDF	${\displaystyle f(x)={\frac {1}{\pi {\sqrt {(x-a)(b-x)}}}}}$
CDF	${\displaystyle F(x)={\frac {2}{\pi }}\arcsin \left({\sqrt {\frac {x-a}{b-a}}}\right)}$
Mean	${\displaystyle {\frac {a+b}{2}}}$
Median	${\displaystyle {\frac {a+b}{2}}}$
Mode	${\displaystyle x\in {a,b}}$
Variance	${\displaystyle {\tfrac {1}{8}}(b-a)^{2}}$
Skewness	${\displaystyle 0}$
Excess kurtosis	${\displaystyle -{\tfrac {3}{2}}}$
CF	${\displaystyle e^{it{\frac {b+a}{2}}}J_{0}({\frac {b-a}{2}}t)}$

Arbitrary bounded support

The distribution can be expanded to include any bounded support from a ≤ x ≤ b by a simple transformation

${\displaystyle F(x)={\frac {2}{\pi }}\arcsin \left({\sqrt {\frac {x-a}{b-a}}}\right)}$

for a ≤ x ≤ b, and whose probability density function is

${\displaystyle f(x)={\frac {1}{\pi {\sqrt {(x-a)(b-x)}}}}}$

on (a, b).

Shape factor

The generalized standard arcsine distribution on (0,1) with probability density function

${\displaystyle f(x;\alpha )={\frac {\sin \pi \alpha }{\pi }}x^{-\alpha }(1-x)^{\alpha -1}}$

is also a special case of the beta distribution with parameters ${\displaystyle {\rm {Beta}}(1-\alpha ,\alpha )}$.

Note that when ${\displaystyle \alpha ={\tfrac {1}{2}}}$ the general arcsine distribution reduces to the standard distribution listed above.

Properties

• Arcsine distribution is closed under translation and scaling by a positive factor
  • If ${\displaystyle X\sim {\rm {Arcsine}}(a,b)\ {\text{then }}kX+c\sim {\rm {Arcsine}}(ak+c,bk+c)}$
• The square of an arcsine distribution over (-1, 1) has arcsine distribution over (0, 1)
  • If ${\displaystyle X\sim {\rm {Arcsine}}(-1,1)\ {\text{then }}X^{2}\sim {\rm {Arcsine}}(0,1)}$
• The coordinates of points uniformly selected on a circle of radius ${\displaystyle r}$ centered at the origin (0, 0), have an ${\displaystyle {\rm {Arcsine}}(-r,r)}$ distribution
  • For example, if we select a point uniformly on the circumference, ${\displaystyle U\sim {\rm {Uniform}}(0,2\pi r)}$, we have that the point's x coordinate distribution is ${\displaystyle r\cdot \cos(U)\sim {\rm {Arcsine}}(-r,r)}$, and its y coordinate distribution is ${\textstyle r\cdot \sin(U)\sim {\rm {Arcsine}}(-r,r)}$

Characteristic function

The characteristic function of the generalized arcsine distribution is a zero order Bessel function of the first kind, multiplied by a complex exponential, given by ${\displaystyle e^{it{\frac {b+a}{2}}}J_{0}({\frac {b-a}{2}}t)}$. For the special case of ${\displaystyle b=-a}$, the characteristic function takes the form of ${\displaystyle J_{0}(bt)}$.

Related distributions

• If U and V are i.i.d uniform (−π,π) random variables, then ${\displaystyle \sin(U)}$, ${\displaystyle \sin(2U)}$, ${\displaystyle -\cos(2U)}$, ${\displaystyle \sin(U+V)}$ and ${\displaystyle \sin(U-V)}$ all have an ${\displaystyle {\rm {Arcsine}}(-1,1)}$ distribution.
• If ${\displaystyle X}$ is the generalized arcsine distribution with shape parameter ${\displaystyle \alpha }$ supported on the finite interval [a,b] then ${\displaystyle {\frac {X-a}{b-a}}\sim {\rm {Beta}}(1-\alpha ,\alpha )\ }$
• If X ~ Cauchy(0, 1) then ${\displaystyle {\tfrac {1}{1+X^{2}}}}$ has a standard arcsine distribution