Top Qs
Timeline
Chat
Perspective
Truncated 6-orthoplexes
From Wikipedia, the free encyclopedia
Remove ads
In six-dimensional geometry, a truncated 6-orthoplex is a convex uniform 6-polytope, being a truncation of the regular 6-orthoplex.
There are 5 degrees of truncation for the 6-orthoplex. Vertices of the truncated 6-orthoplex are located as pairs on the edge of the 6-orthoplex. Vertices of the bitruncated 6-orthoplex are located on the triangular faces of the 6-orthoplex. Vertices of the tritruncated 6-orthoplex are located inside the tetrahedral cells of the 6-orthoplex.
Remove ads
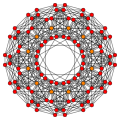
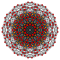
Truncated 6-orthoplex
| Truncated 6-orthoplex | |
|---|---|
| Type | uniform 6-polytope |
| Schläfli symbol | t{3,3,3,3,4} |
| Coxeter-Dynkin diagrams |
|
| 5-faces | 76 |
| 4-faces | 576 |
| Cells | 1200 |
| Faces | 1120 |
| Edges | 540 |
| Vertices | 120 |
| Vertex figure |  ( )v{3,4} |
| Coxeter groups | B6, [3,3,3,3,4] D6, [33,1,1] |
| Properties | convex |
Alternate names
- Truncated hexacross
- Truncated hexacontatetrapeton (Acronym: tag) (Jonathan Bowers)[1]
Construction
There are two Coxeter groups associated with the truncated hexacross, one with the C6 or [4,3,3,3,3] Coxeter group, and a lower symmetry with the D6 or [33,1,1] Coxeter group.
Coordinates
Cartesian coordinates for the vertices of a truncated 6-orthoplex, centered at the origin, are all 120 vertices are sign (4) and coordinate (30) permutations of
- (±2,±1,0,0,0,0)
Images
Remove ads
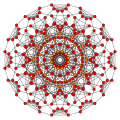
Bitruncated 6-orthoplex
Alternate names
- Bitruncated hexacross
- Bitruncated hexacontatetrapeton (Acronym: botag) (Jonathan Bowers)[2]
Images
Remove ads
Related polytopes
These polytopes are a part of a set of 63 uniform 6-polytopes generated from the B6 Coxeter plane, including the regular 6-cube or 6-orthoplex.
Notes
References
External links
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads