H4 polytope

In 4-dimensional geometry, there are 15 uniform polytopes with H₄ symmetry. Two of these, the 120-cell and 600-cell, are regular.

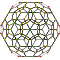
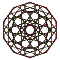
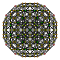
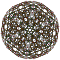
120-cell

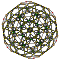
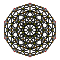
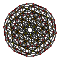
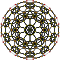
600-cell

Visualizations

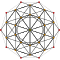
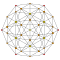
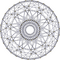
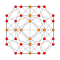
Each can be visualized as symmetric orthographic projections in Coxeter planes of the H₄ Coxeter group, and other subgroups.

The 3D picture are drawn as Schlegel diagram projections, centered on the cell at pos. 3, with a consistent orientation, and the 5 cells at position 0 are shown solid.

#	Name	Coxeter plane projections						Schlegel diagrams		Net
		F4 [12]	[20]	H4 [30]	H3 [10]	A3 [4]	A2 [3]	Dodecahedron centered	Tetrahedron centered
1	120-cell {5,3,3}
2	rectified 120-cell r{5,3,3}
3	rectified 600-cell r{3,3,5}
4	600-cell {3,3,5}
5	truncated 120-cell t{5,3,3}
6	cantellated 120-cell rr{5,3,3}
7	runcinated 120-cell (also runcinated 600-cell) t0,3{5,3,3}
8	bitruncated 120-cell (also bitruncated 600-cell) t1,2{5,3,3}
9	cantellated 600-cell t0,2{3,3,5}
10	truncated 600-cell t{3,3,5}
11	cantitruncated 120-cell tr{5,3,3}
12	runcitruncated 120-cell t0,1,3{5,3,3}
13	runcitruncated 600-cell t0,1,3{3,3,5}
14	cantitruncated 600-cell tr{3,3,5}
15	omnitruncated 120-cell (also omnitruncated 600-cell) t0,1,2,3{5,3,3}

Diminished forms

#	Name	Coxeter plane projections						Schlegel diagrams		Net
		F4 [12]	[20]	H4 [30]	H3 [10]	A3 [4]	A2 [3]	Dodecahedron centered	Tetrahedron centered
16	20-diminished 600-cell (grand antiprism)
17	24-diminished 600-cell (snub 24-cell)
18 Nonuniform	Bi-24-diminished 600-cell
19 Nonuniform	120-diminished rectified 600-cell

Coordinates

The coordinates of uniform polytopes from the H₄ family are complicated. The regular ones can be expressed in terms of the golden ratio φ = (1 + √5)/2 and σ = (3√5 + 1)/2. Coxeter expressed them as 5-dimensional coordinates.^[1]

n	120-cell	600-cell
4D	The 600 vertices of the 120-cell include all permutations of[2] (0, 0, ±2, ±2) (±1, ±1, ±1, ±√5) (±φ−2, ±φ, ±φ, ±φ) (±φ−1, ±φ−1, ±φ−1, ±φ2) and all even permutations of (0, ±φ−2, ±1, ±φ2) (0, ±φ−1, ±φ, ±√5) (±φ−1, ±1, ±φ, ±2)	The vertices of a 600-cell centered at the origin of 4-space, with edges of length 1/φ (where φ = (1+√5)/2 is the golden ratio), can be given as follows: 16 vertices of the form[3] ⁠1/2⁠ (±1, ±1, ±1, ±1), and 8 vertices obtained from (0, 0, 0, ±1) by permuting coordinates. The remaining 96 vertices are obtained by taking even permutations of ⁠1/2⁠ (±φ, ±1, ±1/φ, 0).
5D	Zero-sum permutation: (30): √5 (1, 1, 0, −1, −1) (10): ±(4, −1, −1, −1, −1) (40): ±(φ−1, φ−1, φ−1, 2, −σ) (40): ±(φ, φ, φ, −2, −(σ−1)) (120): ±√5 (φ, 0, 0, φ−1, −1) (120): ±(2, 2, φ−1√5, −φ, −3) (240): ±(φ2, 2φ−1, φ−2, −1, −2φ)	Zero-sum permutation: (20): √5 (1, 0, 0, 0, −1) (40): ±(φ2, φ−2, −1, −1, −1) (60): ±(2, φ−1, φ−1, −φ, −φ)

References

• J.H. Conway and M.J.T. Guy: Four-Dimensional Archimedean Polytopes, Proceedings of the Colloquium on Convexity at Copenhagen, page 38 und 39, 1965
• John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 26)
• H.S.M. Coxeter:
  • H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973
• Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 Wiley::Kaleidoscopes: Selected Writings of H.S.M. Coxeter Archived 2016-07-11 at the Wayback Machine
  • (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
  • (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
  • (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
• N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
• Denney, Tomme; Hooker, Da'Shay; Johnson, De'Janeke; Robinson, Tianna; Butler, Majid; Claiborne, Sandernishe (2020). "The geometry of H4 polytopes". Advances in Geometry. 20 (3): 433–444. arXiv:1912.06156. doi:10.1515/advgeom-2020-0005. S2CID 220367622.
• Dechant, Pierre-Philippe (2021). "Clifford Spinors and Root System Induction: H4 and the Grand Antiprism". Advances in Applied Clifford Algebras. 31 (3). Springer Science and Business Media. arXiv:2103.07817. doi:10.1007/s00006-021-01139-2.