Top Qs
Timeline
Chat
Perspective
Rectified 120-cell
From Wikipedia, the free encyclopedia
Remove ads
In geometry, a rectified 120-cell is a uniform 4-polytope formed as the rectification of the regular 120-cell.
E. L. Elte identified it in 1912 as a semiregular polytope, labeling it as tC120.
There are four rectifications of the 120-cell, including the zeroth, the 120-cell itself. The birectified 120-cell is more easily seen as a rectified 600-cell, and the trirectified 120-cell is the same as the dual 600-cell.
Remove ads
Rectified 120-cell
| Rectified 120-cell | |
|---|---|
 Schlegel diagram, centered on icosidodecahedon, tetrahedral cells visible | |
| Type | Uniform 4-polytope |
| Uniform index | 33 |
| Coxeter diagram | |
| Schläfli symbol | t1{5,3,3} or r{5,3,3} |
| Cells | 720 total: 120 (3.5.3.5) 600 (3.3.3) |
| Faces | 3120 total: 2400 {3}, 720 {5} |
| Edges | 3600 |
| Vertices | 1200 |
| Vertex figure |  triangular prism |
| Symmetry group | H4 or [3,3,5] |
| Properties | convex, vertex-transitive, edge-transitive |

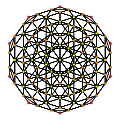
In geometry, the rectified 120-cell or rectified hecatonicosachoron is a convex uniform 4-polytope composed of 600 regular tetrahedra and 120 icosidodecahedra cells. Its vertex figure is a triangular prism, with three icosidodecahedra and two tetrahedra meeting at each vertex.
Alternative names:
- Rectified 120-cell (Norman Johnson)
- Rectified hecatonicosichoron / rectified dodecacontachoron / rectified polydodecahedron
- Icosidodecahedral hexacosihecatonicosachoron
- Rahi (Jonathan Bowers: for rectified hecatonicosachoron)
- Ambohecatonicosachoron (Neil Sloane & John Horton Conway)
Remove ads
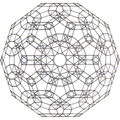
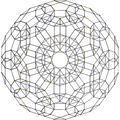
Projections
Remove ads
Related polytopes
Notes
References
External links
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads