Hypersimplex

In polyhedral combinatorics, the hypersimplex ${\displaystyle \Delta _{d,k}}$ is a convex polytope that generalizes the simplex. It is determined by two integers ${\displaystyle d}$ and ${\displaystyle k}$, and is defined as the convex hull of the ${\displaystyle d}$-dimensional vectors whose coefficients consist of ${\displaystyle k}$ ones and ${\displaystyle d-k}$ zeros. Equivalently, ${\displaystyle \Delta _{d,k}}$ can be obtained by slicing the ${\displaystyle d}$-dimensional unit hypercube ${\displaystyle [0,1]^{d}}$ with the hyperplane of equation ${\displaystyle x_{1}+\cdots +x_{d}=k}$ and, for this reason, it is a ${\displaystyle (d-1)}$-dimensional polytope when ${\displaystyle 0<k<d}$.^[1]

Standard hypersimplices in ${\displaystyle \mathbb {R} ^{3}}$

${\displaystyle \Delta _{3,1}}$ Hyperplane: ${\displaystyle x+y+z=1}$	${\displaystyle \Delta _{3,2}}$ Hyperplane: ${\displaystyle x+y+z=2}$

Properties

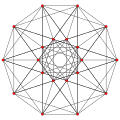
The number of vertices of ${\displaystyle \Delta _{d,k}}$ is ${\displaystyle {\tbinom {d}{k}}}$.^[1] The vertex-edge graph of the hypersimplex ${\displaystyle \Delta _{d,k}}$ is the Johnson graph ${\displaystyle J(d,k)}$.^[2]

Alternative constructions

An alternative construction (for ${\displaystyle 0<k<d}$) is to take the convex hull of all ${\displaystyle (d-1)}$-dimensional ${\displaystyle (0,1)}$-vectors that have either ${\displaystyle k-1}$ or ${\displaystyle k}$ nonzero coordinates. This has the advantage of operating in a space that is the same dimension as the resulting polytope, but the disadvantage that the polytope it produces is less symmetric (although combinatorially equivalent to the result of the other construction).

The hypersimplex ${\displaystyle \Delta _{d,k}}$ is also the matroid polytope for a uniform matroid with ${\displaystyle d}$ elements and rank ${\displaystyle k}$.^[3]

Examples

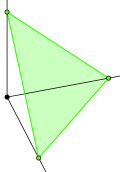
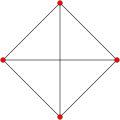
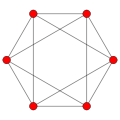
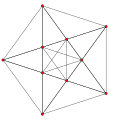
The hypersimplex ${\displaystyle \Delta _{d,1}}$ is a ${\displaystyle (d-1)}$-simplex (and therefore, it has ${\displaystyle d}$ vertices). The hypersimplex ${\displaystyle \Delta _{4,2}}$ is an octahedron, and the hypersimplex ${\displaystyle \Delta _{5,2}}$ is a rectified 5-cell.

Generally, the hypersimplex, ${\displaystyle \Delta _{d,k}}$, corresponds to a uniform polytope, being the ${\displaystyle (k-1)}$-rectified ${\displaystyle (d-1)}$-dimensional simplex, with vertices positioned at the center of all the ${\displaystyle (k-1)}$-dimensional faces of a ${\displaystyle (d-1)}$-dimensional simplex.

Examples (d = 3...6)

Name	Equilateral triangle	Tetrahedron (3-simplex)	Octahedron	5-cell (4-simplex)	Rectified 5-cell	5-simplex	Rectified 5-simplex	Birectified 5-simplex
Δd,k = (d,k) = (d,d − k)	(3,1) (3,2)	(4,1) (4,3)	(4,2)	(5,1) (5,4)	(5,2) (5,3)	(6,1) (6,5)	(6,2) (6,4)	(6,3)
Vertices ${\displaystyle {\tbinom {d}{k}}}$	3	4	6	5	10	6	15	20
d-coordinates	(0,0,1) (0,1,1)	(0,0,0,1) (0,1,1,1)	(0,0,1,1)	(0,0,0,0,1) (0,1,1,1,1)	(0,0,0,1,1) (0,0,1,1,1)	(0,0,0,0,0,1) (0,1,1,1,1,1)	(0,0,0,0,1,1) (0,0,1,1,1,1)	(0,0,0,1,1,1)
Image
Graphs	J(3,1) = K2	J(4,1) = K3	J(4,2) = T(6,3)	J(5,1) = K4	J(5,2)	J(6,1) = K5	J(6,2)	J(6,3)
Coxeter diagrams
Schläfli symbols	{3} = r{3}	{3,3} = 2r{3,3}	r{3,3} = {3,4}	{3,3,3} = 3r{3,3,3}	r{3,3,3} = 2r{3,3,3}	{3,3,3,3} = 4r{3,3,3,3}	r{3,3,3,3} = 3r{3,3,3,3}	2r{3,3,3,3}
Facets	{ }	{3}		{3,3}	{3,3}, {3,4}	{3,3,3}	{3,3,3}, r{3,3,3}	r{3,3,3}

History

The hypersimplices were first studied and named in the computation of characteristic classes (an important topic in algebraic topology), by Gabrièlov, Gelʹfand & Losik (1975).^[4][5]