Hypotrochoid

In geometry, a hypotrochoid is a roulette traced by a point attached to a circle of radius r rolling around the inside of a fixed circle of radius R, where the point is a distance d from the center of the interior circle.

The red curve is a hypotrochoid drawn as the smaller black circle rolls around inside the larger blue circle (parameters are R = 5, r = 3, d = 5).

The parametric equations for a hypotrochoid are:^[1]

${\displaystyle {\begin{aligned}&x(\theta )=(R-r)\cos \theta +d\cos \left({R-r \over r}\theta \right)\\&y(\theta )=(R-r)\sin \theta -d\sin \left({R-r \over r}\theta \right)\end{aligned}}}$

where θ is the angle formed by the horizontal and the center of the rolling circle (these are not polar equations because θ is not the polar angle). When measured in radian, θ takes values from 0 to ${\displaystyle 2\pi \times {\tfrac {\operatorname {LCM} (r,R)}{R}}}$ (where LCM is least common multiple).

Special cases include the hypocycloid with d = r and the ellipse with R = 2r and d ≠ r.^[2] The eccentricity of the ellipse is

${\displaystyle e={\frac {2{\sqrt {d/r}}}{1+(d/r)}}}$

becoming 1 when ${\displaystyle d=r}$ (see Tusi couple).

The ellipse (drawn in red) may be expressed as a special case of the hypotrochoid, with R = 2r (Tusi couple); here R = 10, r = 5, d = 1.

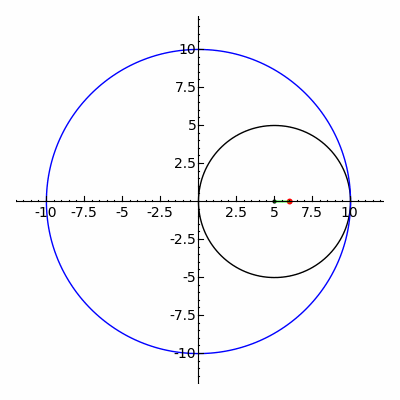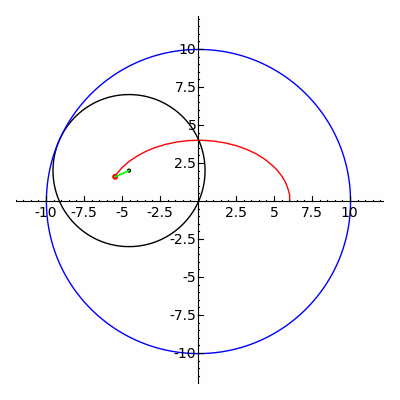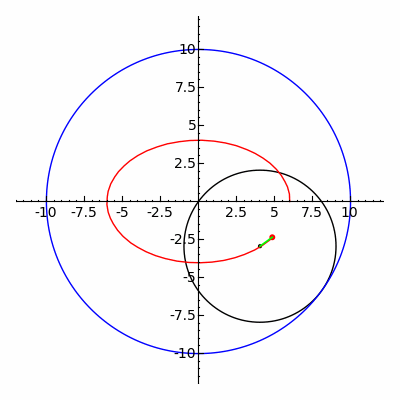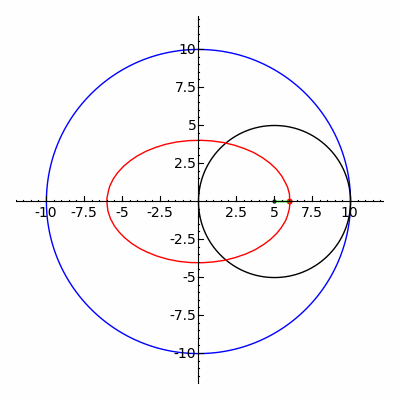
The classic Spirograph toy traces out hypotrochoid and epitrochoid curves.

Hypotrochoids describe the support of the eigenvalues of some random matrices with cyclic correlations.^[3]

See also

• Cycloid
• Cyclogon
• Epicycloid
• Rosetta (orbit)
• Apsidal precession
• Spirograph