Top Qs
Timeline
Chat
Perspective
List of geodesic polyhedra and Goldberg polyhedra
From Wikipedia, the free encyclopedia
Remove ads
This is a dynamic list and may never be able to satisfy particular standards for completeness. You can help by editing the page to add missing items, with references to reliable sources.
This is a list of selected geodesic polyhedra and Goldberg polyhedra, two infinite classes of polyhedra. Geodesic polyhedra and Goldberg polyhedra are duals of each other. The geodesic and Goldberg polyhedra are parameterized by integers m and n, with 


Remove ads
Icosahedral
Summarize
Perspective
More information m, n ...
| m | n | T | Class | Vertices (geodesic) Faces (Goldberg) |
Edges | Faces (geodesic) Vertices (Goldberg) |
Face triangle |
Geodesic | Goldberg | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Symbols | Conway | Image | Symbols | Conway | Image | ||||||||
| 1 | 0 | 1 | I | 12 | 30 | 20 |  | {3,5} {3,5+}1,0 | I |  | {5,3} {5+,3}1,0 GP5(1,0) | D |  |
| 2 | 0 | 4 | I | 42 | 120 | 80 |  | {3,5+}2,0 | uI dcdI |  | {5+,3}2,0 GP5(2,0) | cD cD |  |
| 3 | 0 | 9 | I | 92 | 270 | 180 |  | {3,5+}3,0 | xI ktI |  | {5+,3}3,0 GP5(3,0) | yD tkD |  |
| 4 | 0 | 16 | I | 162 | 480 | 320 |  | {3,5+}4,0 | uuI dccD |  | {5+,3}4,0 GP5(4,0) | c2D |  |
| 5 | 0 | 25 | I | 252 | 750 | 500 |  | {3,5+}5,0 | u5I |  | {5+,3}5,0 GP5(5,0) | c5D du5I |  |
| 6 | 0 | 36 | I | 362 | 1080 | 720 |  | {3,5+}6,0 | uxI dctkdI |  | {5+,3}6,0 GP5(6,0) | cyD ctkD |  |
| 7 | 0 | 49 | I | 492 | 1470 | 980 | 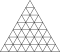 | {3,5+}7,0 | vvI dwrwdI |  | {5+,3}7,0 GP5(7,0) | wwD wrwD |  |
| 8 | 0 | 64 | I | 642 | 1920 | 1280 | 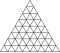 | {3,5+}8,0 | u3I dcccdI |  | {5+,3}8,0 GP5(8,0) | cccD |  |
| 9 | 0 | 81 | I | 812 | 2430 | 1620 | 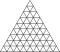 | {3,5+}9,0 | xxI ktktI |  | {5+,3}9,0 GP5(9,0) | yyD tktkD |  |
| 10 | 0 | 100 | I | 1002 | 3000 | 2000 |  | {3,5+}10,0 | uu5I |  | {5+,3}10,0 GP5(10,0) | cc5D cdu5I | 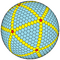 |
| 11 | 0 | 121 | I | 1212 | 3630 | 2420 |  | {3,5+}11,0 | u11I |  | {5+,3}11,0 GP5(11,0) | c11D | |
| 12 | 0 | 144 | I | 1442 | 4320 | 2880 |  | {3,5+}12,0 | uuxD dcctkD |  | {5+,3}12,0 GP5(12,0) | ccyD cctkD | 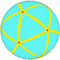 |
| 13 | 0 | 169 | I | 1692 | 5070 | 3380 |  | {3,5+}13,0 | u13I |  | {5+,3}13,0 GP5(13,0) | c13D | |
| 14 | 0 | 196 | I | 1962 | 5880 | 3920 |  | {3,5+}14,0 | uvvI dcwwdI |  | {5+,3}14,0 GP5(14,0) | cwrwD |  |
| 15 | 0 | 225 | I | 2252 | 6750 | 4500 |  | {3,5+}15,0 | u5xI u5ktI |  | {5+,3}15,0 GP5(15,0) | c5yD c5tkD du5ktI |  |
| 16 | 0 | 256 | I | 2562 | 7680 | 5120 |  | {3,5+}16,0 | dc4dI |  | {5+,3}16,0 GP5(16,0) | ccccD |  |
| 1 | 1 | 3 | II | 32 | 90 | 60 |  | {3,5+}1,1 | nI kD |  | {5+,3}1,1 GP5(1,1) | yD tI |  |
| 2 | 2 | 12 | II | 122 | 360 | 240 |  | {3,5+}2,2 | unI =dctI |  | {5+,3}2,2 GP5(2,2) | czD cdkD |  |
| 3 | 3 | 27 | II | 272 | 810 | 540 |  | {3,5+}3,3 | xnI ktkD | 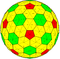 | {5+,3}3,3 GP5(3,3) | yzD tkdkD |  |
| 4 | 4 | 48 | II | 482 | 1440 | 960 |  | {3,5+}4,4 | u2nI dcctI |  | {5+,3}4,4 GP5(4,4) | c2zD cctI |  |
| 5 | 5 | 75 | II | 752 | 2250 | 1500 |  | {3,5+}5,5 | u5nI |  | {5+,3}5,5 GP5(5,5) | c5zD |  |
| 6 | 6 | 108 | II | 1082 | 3240 | 2160 |  | {3,5+}6,6 | uxnI dctktI | {5+,3}6,6 GP5(6,6) | cyzD ctkdkD | 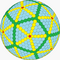 | |
| 7 | 7 | 147 | II | 1472 | 4410 | 2940 |  | {3,5+}7,7 | vvnI dwrwtI |  | {5+,3}7,7 GP5(7,7) | wwzD wrwdkD |  |
| 8 | 8 | 192 | II | 1922 | 5760 | 3840 |  | {3,5+}8,8 | u3nI dccckD |  | {5+,3}8,8 GP5(8,8) | c3zD ccctI |  |
| 9 | 9 | 243 | II | 2432 | 7290 | 4860 |  | {3,5+}9,9 | xxnI ktktkD |  | {5+,3}9,9 GP5(9,9) | yyzD tktktI |  |
| 12 | 12 | 432 | II | 4322 | 12960 | 8640 |  | {3,5+}12,12 | uuxnI dccdktkD |  | {5+,3}12,12 GP5(12,12) | ccyzD cckttI |  |
| 14 | 14 | 588 | II | 5882 | 17640 | 11760 |  | {3,5+}14,14 | uvvnI dcwwkD |  | {5+,3}14,14 GP5(14,14) | cwwzD cwrwtI |  |
| 16 | 16 | 768 | II | 7682 | 23040 | 15360 |  | {3,5+}16,16 | uuuunI dcccctI |  | {5+,3}16,16 GP5(16,16) | cccczD cccctI |  |
| 2 | 1 | 7 | III | 72 | 210 | 140 |  | {3,5+}2,1 | vI dwD |  |
{5+,3}2,1 GP5(2,1) | wD | 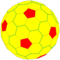 |
| 3 | 1 | 13 | III | 132 | 390 | 260 | 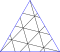 | {3,5+}3,1 | v3,1I |  | {5+,3}3,1 GP5(3,1) | w3,1D |  |
| 3 | 2 | 19 | III | 192 | 570 | 380 |  | {3,5+}3,2 | v3I |  | {5+,3}3,2 GP5(3,2) | w3D |  |
| 4 | 1 | 21 | III | 212 | 630 | 420 |  | {3,5+}4,1 | dwtI |  | {5+,3}4,1 GP5(4,1) | wdkD |  |
| 4 | 2 | 28 | III | 282 | 840 | 560 |  | {3,5+}4,2 | vnI dwtI |  | {5+,3}4,2 GP5(4,2) | wcD |  |
| 4 | 3 | 37 | III | 372 | 1110 | 740 |  | {3,5+}4,3 | v4I | {5+,3}4,3 GP5(4,3) | w4D |  | |
| 5 | 1 | 31 | III | 312 | 930 | 620 |  | {3,5+}5,1 | u5,1I | {5+,3}5,1 GP5(5,1) | w5,1D |  | |
| 5 | 2 | 39 | III | 392 | 1170 | 780 |  | {3,5+}5,2 | u5,2I |  | {5+,3}5,2 GP5(5,2) | w5,2D |  |
| 5 | 3 | 49 | III | 492 | 1470 | 980 |  | {3,5+}5,3 | vvI dwwD |  | {5+,3}5,3 GP5(5,3) | wwD |  |
| 5 | 4 | 61 | III | 612 | 1830 | 1220 |  | {3,5+}5,4 | u5,4I |  | {5+,3}5,4 GP5(5,4) | w5,4D |  |
| 6 | 2 | 52 | III | 522 | 1560 | 1040 |  | {3,5+}6,2 | v3,1uI |  | {5+,3}6,2 GP5(6,2) | w3,1cD |  |
| 6 | 3 | 63 | III | 632 | 1890 | 1260 |  | {3,5+}6,3 | vxI dwdktI |  | {5+,3}6,3 GP5(6,3) | wyD wtkD |  |
| 8 | 2 | 84 | III | 842 | 2520 | 1680 |  | {3,5+}8,2 | vunI dwctI | {5+,3}8,2 GP5(8,2) | wczD wcdkD |  | |
| 8 | 4 | 112 | III | 1122 | 3360 | 2240 |  | {3,5+}8,4 | vuuI dwccD | {5+,3}8,4 GP5(8,4) | wccD |  | |
| 11 | 2 | 147 | III | 1472 | 4410 | 2940 |  | {3,5+}11,2 | vvnI dwwtI | {5+,3}11,2 GP5(11,2) | wwzD |  | |
| 12 | 3 | 189 | III | 1892 | 5670 | 3780 |  | {3,5+}12,3 | vxnI dwtktktI | {5+,3}12,3 GP5(12,3) | wyzD wtktI |  | |
| 10 | 6 | 196 | III | 1962 | 5880 | 3920 |  | {3,5+}10,6 | vvuI dwwcD | {5+,3}10,6 GP5(10,6) | wwcD |  | |
| 12 | 6 | 252 | III | 2522 | 7560 | 5040 |  | {3,5+}12,6 | vxuI dwctkD | {5+,3}12,6 GP5(12,6) | cywD wctkD |  | |
| 16 | 4 | 336 | III | 3362 | 10080 | 6720 | 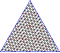 | {3,5+}16,4 | vuunI dwcctI | {5+,3}16,4 GP5(16,4) | wcczD wcctI |  | |
| 14 | 7 | 343 | III | 3432 | 10290 | 6860 |  | {3,5+}14,7 | vvvI dwrwwD | {5+,3}14,7 GP5(14,7) | wwwD wrwwD |  | |
| 15 | 9 | 441 | III | 4412 | 13230 | 8820 |  | {3,5+}15,9 | vvxI dwwtkD | {5+,3}15,9 GP5(15,9) | wwxD wwtkD |  | |
| 16 | 8 | 448 | III | 4482 | 13440 | 8960 |  | {3,5+}16,8 | vuuuI dwcccD | {5+,3}16,8 GP5(16,8) | wcccD |  | |
| 18 | 1 | 343 | III | 3432 | 10290 | 6860 | {3,5+}18,1 | vvvI dwwwD | {5+,3}18,1 GP5(18,1) | wwwD |  | ||
| 18 | 9 | 567 | III | 5672 | 17010 | 11340 | {3,5+}18,9 | vxxI dwtktkD | {5+,3}18,9 GP5(18,9) | wyyD wtktkD |  | ||
| 20 | 12 | 784 | III | 7842 | 23520 | 15680 | {3,5+}20,12 | vvuuI dwwccD | {5+,3}20,12 GP5(20,12) | wwccD |  | ||
| 20 | 17 | 1029 | III | 10292 | 30870 | 20580 | {3,5+}20,17 | vvvnI dwwwtI | {5+,3}20,17 GP5(20,17) | wwwzD wwwdkD |  | ||
| 28 | 7 | 1029 | III | 10292 | 30870 | 20580 | {3,5+}28,7 | vvvnI dwrwwdkD | {5+,3}28,7 GP5(28,7) | wwwzD wrwwdkD |  | ||
Close
Remove ads
Octahedral
More information m, n ...
| m | n | T | Class | Vertices (geodesic) Faces (Goldberg) |
Edges | Faces (geodesic) Vertices (Goldberg) |
Face triangle |
Geodesic | Goldberg | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Symbols | Conway | Image | Symbols | Conway | Image | ||||||||
| 1 | 0 | 1 | I | 6 | 12 | 8 |  | {3,4} {3,4+}1,0 | O |  | {4,3} {4+,3}1,0 GP4(1,0) | C |  |
| 2 | 0 | 4 | I | 18 | 48 | 32 |  | {3,4+}2,0 | dcC dcC |  | {4+,3}2,0 GP4(2,0) | cC cC | 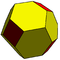 |
| 3 | 0 | 9 | I | 38 | 108 | 72 |  | {3,4+}3,0 | ktO |  | {4+,3}3,0 GP4(3,0) | tkC | 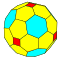 |
| 4 | 0 | 16 | I | 66 | 192 | 128 |  | {3,4+}4,0 | uuO dccC | 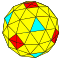 | {4+,3}4,0 GP4(4,0) | ccC | 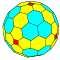 |
| 5 | 0 | 25 | I | 102 | 300 | 200 |  | {3,4+}5,0 | u5O | 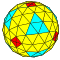 | {4+,3}5,0 GP4(5,0) | c5C |  |
| 6 | 0 | 36 | I | 146 | 432 | 288 |  | {3,4+}6,0 | uxO dctkdO | 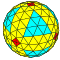 | {4+,3}6,0 GP4(6,0) | cyC ctkC |  |
| 7 | 0 | 49 | I | 198 | 588 | 392 |  | {3,4+}7,0 | dwrwO | 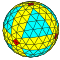 | {4+,3}7,0 GP4(7,0) | wrwO |  |
| 8 | 0 | 64 | I | 258 | 768 | 512 |  | {3,4+}8,0 | uuuO dcccC | 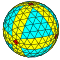 | {4+,3}8,0 GP4(8,0) | cccC | 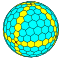 |
| 9 | 0 | 81 | I | 326 | 972 | 648 |  | {3,4+}9,0 | xxO ktktO |  | {4+,3}9,0 GP4(9,0) | yyC tktkC |  |
| 1 | 1 | 3 | II | 14 | 36 | 24 |  | {3,4+}1,1 | kC |  | {4+,3}1,1 GP4(1,1) | tO |  |
| 2 | 2 | 12 | II | 50 | 144 | 96 |  | {3,4+}2,2 | ukC dctO | {4+,3}2,2 GP4(2,2) | czC ctO |  | |
| 3 | 3 | 27 | II | 110 | 324 | 216 |  | {3,4+}3,3 | ktkC | {4+,3}3,3 GP4(3,3) | tktO |  | |
| 4 | 4 | 48 | II | 194 | 576 | 384 |  | {3,4+}4,4 | uunO dcctO | {4+,3}4,4 GP4(4,4) | cczC cctO |  | |
| 2 | 1 | 7 | III | 30 | 84 | 56 |  | {3,4+}2,1 | vO dwC |  | {4+,3}2,1 GP4(2,1) | wC | 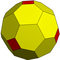 |
Close
Remove ads
Tetrahedral
More information m, n ...
| m | n | T | Class | Vertices (geodesic) Faces (Goldberg) |
Edges | Faces (geodesic) Vertices (Goldberg) |
Face triangle |
Geodesic | Goldberg | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Symbols | Conway | Image | Symbols | Conway | Image | ||||||||
| 1 | 0 | 1 | I | 4 | 6 | 4 |  | {3,3} {3,3+}1,0 | T |  | {3,3} {3+,3}1,0 GP3(1,0) | T |  |
| 1 | 1 | 3 | II | 8 | 18 | 12 |  | {3,3+}1,1 | kT kT |  | {3+,3}1,1 GP3(1,1) | tT tT |  |
| 2 | 0 | 4 | I | 10 | 24 | 16 |  | {3,3+}2,0 | dcT dcT |  | {3+,3}2,0 GP3(2,0) | cT cT |  |
| 3 | 0 | 9 | I | 20 | 54 | 36 |  | {3,3+}3,0 | ktT | 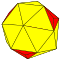 | {3+,3}3,0 GP3(3,0) | tkT |  |
| 4 | 0 | 16 | I | 34 | 96 | 64 |  | {3,3+}4,0 | uuT dccT | 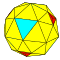 | {3+,3}4,0 GP3(4,0) | ccT |  |
| 5 | 0 | 25 | I | 52 | 150 | 100 |  | {3,3+}5,0 | u5T |  | {3+,3}5,0 GP3(5,0) | c5T |  |
| 6 | 0 | 36 | I | 74 | 216 | 144 |  | {3,3+}6,0 | uxT dctkdT | 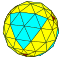 | {3+,3}6,0 GP3(6,0) | cyT ctkT | 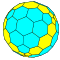 |
| 7 | 0 | 49 | I | 100 | 294 | 196 |  | {3,3+}7,0 | vrvT dwrwT |  | {3+,3}7,0 GP3(7,0) | wrwT |  |
| 8 | 0 | 64 | I | 130 | 384 | 256 |  | {3,3+}8,0 | u3T dcccdT |  | {3+,3}8,0 GP3(8,0) | c3T cccT |  |
| 9 | 0 | 81 | I | 164 | 486 | 324 |  | {3,3+}9,0 | xxT ktktT | 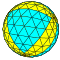 | {3+,3}9,0 GP3(9,0) | yyT tktkT | 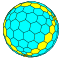 |
| 3 | 3 | 27 | II | 56 | 162 | 108 |  | {3,3+}3,3 | ktkT | {3+,3}3,3 GP3(3,3) | tktT |  | |
| 2 | 1 | 7 | III | 16 | 42 | 28 |  | {3,3+}2,1 | dwT |  | {3+,3}2,1 GP5(2,1) | wT |  |
Close
References
- Wenninger, Magnus (1979), Spherical Models, Cambridge University Press, ISBN 978-0-521-29432-4, MR 0552023, archived from the original on July 4, 2008 Reprinted by Dover 1999 ISBN 978-0-486-40921-4
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads
Remove ads