Top Qs
Timeline
Chat
Perspective
Angle
Figure formed by two rays meeting at a common point From Wikipedia, the free encyclopedia
Remove ads
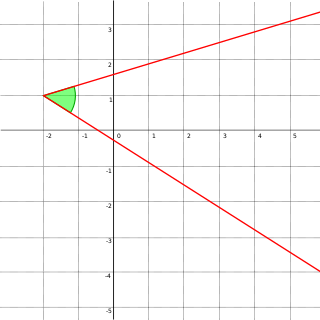
In geometry, an angle is formed by two lines that meet at a point.[1] Each line is called a side of the angle, and the point they share is called the vertex of the angle.[2][3] The term angle is used to denote both geometric figures and their size or magnitude as associated quantity. Angular measure or measure of angle are sometimes used to distinguish between the measure of the quantity and figure itself. The measurement of angles is intrinsically linked with circles and rotation, and this is often visualized or defined using the arc of a circle centered at the vertex and lying between the sides.
Remove ads
Fundamentals
Summarize
Perspective
There is no universally agreed definition of an angle.[4] Angles can be conceived of and used in a variety of ways and while valid definitions may be given for specific contexts, it is difficult to give a single formal definition that is completely satisfactory in capturing all aspects of the general concept of angle.[5]
One standard definition is that an angle is a figure consisting of two rays which lie in a plane and share a common endpoint. Alternatively, given such a figure, an angle might be defined as: the opening between the rays; the area of the plane that lies between the rays; or the amount of rotation about the vertex of one ray to the other.
More generally, angles are also formed wherever two line segments come together, such as at the corners of triangles and other polygons,[2] or at the intersection of two planes or curves, in which case the rays lying tangent to each curve at the point of intersection define the angle.[6]
It is common to consider that the sides of the angle divide the plane into two regions called the interior of the angle and the exterior of the angle. The interior of the angle is also referred to as an angular sector.[7][8][a]
Notation and measurement

An angle symbol ( or , read as "angle") together with one or three defining points is used to identify angles in geometric figures. For example, the angle with vertex A formed by the rays and is denoted as (using the vertex alone) or (with the vertex always named in the middle). The size or measure of the angle is denoted or .
In geometric figures and mathematical expressions, it is also common to use Greek letters (α, β, γ, θ, φ, ...) or lower case Roman letters (a, b, c, ...) as variables to represent the size of an angle.[12] Angular measure is commonly a scalar quantity,[13] although in physics and some fields of mathematics, signed angles are used by convention to indicate a direction of rotation: positive for anti-clockwise; negative for clockwise.[14]
Units of measurement
Angles are measured in various units, the most common being the degree (denoted by the symbol °), radian (denoted by the symbol rad) and turn. These units differ in the way they divide up a full angle, an angle where one ray, initially congruent to the other, performs a compete rotation about the vertex to return back to its starting position.[15]
Degrees and turns are defined directly with reference to a full angle, which measures 1 turn or 360°.[16] A measure in turns gives an angle's size as a proportion of a full angle and a degree can be considered as a subdivision of a turn. Radians are not defined directly in relation to a full angle (see § Measuring angles), but in such a way that its measure is 2π rad, approximately 6.28 rad.[17]
Historically the degree unit was chosen such as the straight angle or half the full angle was attributed the value of 180.
Addition and subtraction

The angle addition postulate states that if D is a point lying in the interior of then:[18] This relationship defines what it means to add any two angles: their vertices are placed together while sharing a side to create a new larger angle. The measure of the new larger angle is the sum of the measures of the two angles. Subtraction follows from rearrangement of the formula.[18]
Remove ads
Types
Summarize
Perspective
Common angles

- An angle equal to 0° or not turned is called a zero angle.[19]
- An angle smaller than a right angle (less than 90°) is called an acute angle.[20]
- An angle equal to 1/4 turn (90° or π/2 rad) is called a right angle. Two lines that form a right angle are said to be normal, orthogonal, or perpendicular.[21]
- An angle larger than a right angle and smaller than a straight angle (between 90° and 180°) is called an obtuse angle[20] ("obtuse" meaning "blunt").
- An angle equal to 1/2 turn (180° or π rad) is called a straight angle.[19]
- An angle larger than a straight angle but less than 1 turn (between 180° and 360°) is called a reflex angle.
- An angle equal to 1 turn (360° or 2π rad) is called a full angle, complete angle, round angle or perigon.
- An angle that is not a multiple of a right angle is called an oblique angle.
Adjacent and vertical angles
- Angles A and B are adjacent.
- Angles A and B, and pair C and D are two pairs of vertical angles. Hatch marks indicate equality between pairs.
Adjacent angles (abbreviated adj. ∠s), are angles that share a common vertex and edge but do not share any interior points. In other words, they are angles side by side or adjacent, sharing an "arm".
Vertical angles are formed when two straight lines intersect at a point producing four angles. A pair of angles opposite each other are called vertical angles, opposite angles or vertically opposite angles (abbreviated vert. opp. ∠s),[22] where "vertical" refers to the sharing of a vertex, rather than an up-down orientation. A theorem states that vertical angles are always congruent or equal to each other.[23] A transversal is a line that intersects a pair of (often parallel) lines and is associated with exterior angles, interior angles, alternate exterior angles, alternate interior angles, corresponding angles, and consecutive interior angles.[24]
Combining angle pairs
When summing two angles (either adjacent or separated in space), three special cases are named complementary, supplementary, and explementary angles.
Complementary angles are angle pairs whose measures sum to a right angle (1/4 turn, 90°, or π/2 rad). If the two complementary angles are adjacent, their non-shared sides form a right angle. In a right-angle triangle the two acute angles are complementary as the sum of the internal angles of a triangle is 180°. The difference between an angle and a right angle is termed the complement of the angle.[6]
Supplementary angles sum to a straight angle (1/2 turn, 180°, or π rad). If the two supplementary angles are adjacent, their non-shared sides form a straight angle or straight line and are called a linear pair of angles.[25] The difference between an angle and a straight angle is termed the supplement of the angle.[26]
Explementary angles or conjugate angles sum to a full angle (1 turn, 360°, or 2π radians).[27] The difference between an angle and a full angle is termed the explement or conjugate of the angle.[28][29]
Examples of non-adjacent supplementary angles include the consecutive angles of a parallelogram and opposite angles of a cyclic quadrilateral. For a circle with center O, and tangent lines from an exterior point P touching the circle at points T and Q, the resulting angles ∠TPQ and ∠TOQ are supplementary.
- Angles
aandbare complementary angles - Angles
aandbare supplementary angles - Angles
AOBandCODare explementary or conjugate angles
Polygon-related angles

- An angle that is part of a simple polygon is called an interior angle if it lies on the inside of that simple polygon. A simple concave polygon has at least one interior angle, that is, a reflex angle. In Euclidean geometry, the measures of the interior angles of a triangle add up to π radians, 180°, or 1/2 turn; the measures of the interior angles of a simple convex quadrilateral add up to 2π radians, 360°, or 1 turn. In general, the measures of the interior angles of a simple convex polygon with n sides add up to (n − 2)π radians, or (n − 2)180 degrees, (n − 2)2 right angles, or (n − 2)1/2 turn.
- The supplement of an interior angle is called an exterior angle; that is, an interior angle and an exterior angle form a linear pair of angles. There are two exterior angles at each vertex of the polygon, each determined by extending one of the two sides of the polygon that meet at the vertex; these two angles are vertical and hence are equal. An exterior angle measures the amount of rotation one must make at a vertex to trace the polygon.[30] If the corresponding interior angle is a reflex angle, the exterior angle should be considered negative. Even in a non-simple polygon, it may be possible to define the exterior angle. Still, one will have to pick an orientation of the plane (or surface) to decide the sign of the exterior angle measure. In Euclidean geometry, the sum of the exterior angles of a simple convex polygon, if only one of the two exterior angles is assumed at each vertex, will be one full turn (360°). The exterior angle here could be called a supplementary exterior angle. Exterior angles are commonly used in Logo Turtle programs when drawing regular polygons.
- In a triangle, the bisectors of two exterior angles and the bisector of the other interior angle are concurrent (meet at a single point).[31]: 149
- In a triangle, three intersection points, each of an external angle bisector with the opposite extended side, are collinear.[31]: 149
- In a triangle, three intersection points, two between an interior angle bisector and the opposite side, and the third between the other exterior angle bisector and the opposite side extended are collinear.[31]: 149
- Some authors use the name exterior angle of a simple polygon to mean the explement exterior angle (not supplement!) of the interior angle.[32] This conflicts with the above usage.
Plane-related angles
- The angle between two planes (such as two adjacent faces of a polyhedron) is called a dihedral angle.[6] It may be defined as the acute angle between two lines normal to the planes.
- The angle between a plane and an intersecting straight line is complementary to the angle between the intersecting line and the normal to the plane.
Remove ads
Measuring angles
Summarize
Perspective
Angle measurement encompasses both direct physical measurement using a measuring instrument such as a protractor, as well as the theoretical calculation of angle size from other known quantities. While the measurement of angles is intrinsically linked with rotation and circles, there are various perspectives as to exactly what is being measured, including amongst others: the amount of rotation about the vertex of one ray to the other;[33] the amount of opening between the rays;[34] or the length of the arc that subtends the angle at the centre of a unit circle.[35]
The measurement of angles is inherently different from the measurement of other physical quantities such as length.[36] Angles of special significance (such as the right angle) inform the systems and units of angular measurement, which is not the case for length where the units of measurement (metres, feet) are arbitrary.
Broadly there are two approaches to measuring angles: relative to a reference angle (such as a right angle); and circular measurement.
Reference angle
A chosen reference angle (right angle, straight angle or full angle) can be divided into equal parts, and the size of one part used as a unit for measurement of other angles.
In the most common method of practical angular measurement a right angle is divided into 90 equal parts called degrees, while in the rarely used centesimal system, a right angle is divided into 100 equal parts called gradians.[37][38]
Circular measurement

With circular measurement an angle is placed within a circle of any size, with the vertex at the circle's centre and the sides intersecting the perimeter.
An arc with length s is formed as the perimeter between the two points of intersection, which is said to subtend the angle. The length s can be used to measure the angle's size θ, however as s is dependent on the size of the circle chosen, the measure must be scaled. This can be done by taking the ratio of s to either the radius r or circumference C of the circle.
The ratio of the length s by the radius r is the number of radians in the angle,[35] while the ratio of length s by the circumference C is the number of turns:

The value of θ thus defined is independent of the size of the circle: if the length of the radius is changed, then both the circumference and the arc length change in the same proportion, so the ratios s/r and s/C are unaltered.[nb 1]
The ratio s/r is called the "radian measure"[18] or "circular measure"[39][38][40] of an angle, but is also used to define a unit of measurement called a radian, which is defined as an angle for which the ratio s/r = 1.[39] Thus, the measurement of an angle given by s/r can be thought of in two ways: firstly as a measure in terms of the angle's own proportions (ratio of arc length to radius), or secondly as the quantity of units in the angle (ratio of arc length of measured angle to arc length of unit angle).[41][38]
Units
The following table lists some notable units used to represent angles.
Dimensional analysis
In mathematics and the International System of Quantities, an angle is defined as a dimensionless quantity,[42] and in particular, the radian is defined as dimensionless in the International System of Units.[43] This convention prevents angles providing information for dimensional analysis. For example, when one measures an angle in radians by dividing the arc length by the radius, one is essentially dividing a length by another length, and the units of length cancel each other out. Therefore the result—the angle—doesn't have a physical "dimension" like meters or seconds.[44] This holds true with all angle units, such as radians, degrees, or turns—they all represent a pure number quantifying how much something has turned.[45] This is why, in many equations, angle units seem to "disappear" during calculations, which feels inconsistent and can lead to mixing up angle units.[46][47]
This has led to significant discussion among scientists and educators. Some scientists have suggested treating the angle as having its own fundamental dimension, similar to length or time.[48] This would mean that angle units like radians would always be explicitly present in calculations, facilitating dimensional analysis. However, this approach would also require changing many well-known mathematical and physics formulas, making them longer and perhaps a bit less familiar.[49] For now, the established practice is to write angle units where appropriate but consider them dimensionless, understanding that these units are important but behave differently from meters or kilograms.[50]
Signed angles

An angle denoted as ∠BAC might refer to any of four angles: the clockwise angle from B to C about A, the anticlockwise angle from B to C about A, the clockwise angle from C to B about A, or the anticlockwise angle from C to B about A, It is therefore frequently helpful to impose a convention that allows positive and negative angular values to represent orientations and/or rotations in opposite directions or "sense" relative to some reference.
In a two-dimensional Cartesian coordinate system, an angle is typically defined by its two sides, with its vertex at the origin. The initial side is on the positive x-axis, while the other side or terminal side is defined by the measure from the initial side in radians, degrees, or turns, with positive angles representing rotations toward the positive y-axis and negative angles representing rotations toward the negative y-axis. When Cartesian coordinates are represented by standard position, defined by the x-axis rightward and the y-axis upward, positive rotations are anticlockwise, and negative cycles are clockwise.
In many contexts, an angle of −θ is effectively equivalent to an angle of "one full turn minus θ". For example, an orientation represented as −45° is effectively equal to an orientation defined as 360° − 45° or 315°. Although the final position is the same, a physical rotation (movement) of −45° is not the same as a rotation of 315° (for example, the rotation of a person holding a broom resting on a dusty floor would leave visually different traces of swept regions on the floor).
In three-dimensional geometry, "clockwise" and "anticlockwise" have no absolute meaning, so the direction of positive and negative angles must be defined in terms of an orientation, which is typically determined by a normal vector passing through the angle's vertex and perpendicular to the plane in which the rays of the angle lie.
In navigation, bearings or azimuth are measured relative to north. By convention, viewed from above, bearing angles are positive clockwise, so a bearing of 45° corresponds to a north-east orientation. Negative bearings are not used in navigation, so a north-west orientation corresponds to a bearing of 315°.
Equivalent angles
- Angles that have the same measure (i.e., the same magnitude) are said to be equal or congruent. An angle is defined by its measure and is not dependent upon the lengths of the sides of the angle (e.g., all right angles are equal in measure).
- Two angles that share terminal sides, but differ in size by an integer multiple of a turn, are called coterminal angles.
- The reference angle (sometimes called related angle) for any angle θ in standard position is the positive acute angle between the terminal side of θ and the x-axis (positive or negative).[51] Procedurally, the magnitude of the reference angle for a given angle may determined by taking the angle's magnitude modulo 1/2 turn, 180°, or π radians, then stopping if the angle is acute, otherwise taking the supplementary angle, 180° minus the reduced magnitude. For example, an angle of 30 degrees is already a reference angle, and an angle of 150 degrees also has a reference angle of 30 degrees (180° − 150°). Angles of 210° and 510° correspond to a reference angle of 30 degrees as well (210° mod 180° = 30°, 510° mod 180° = 150° whose supplementary angle is 30°).
Related quantities
For an angular unit, it is definitional that the angle addition postulate holds, however some measurements or quantities related to angles are in use that do not satisfy this postulate:
- The slope or gradient is equal to the tangent of the angle and is often expressed as a percentage ("rise" over "run"). For very small values (less than 5%), the slope of a line is approximately the measure in radians of its angle with the horizontal direction. An elevation grade is a slope used to indicate the steepness of roads, paths and railway lines.
- The spread between two lines is defined in rational geometry as the square of the sine of the angle between the lines. As the sine of an angle and the sine of its supplementary angle are the same, any angle of rotation that maps one of the lines into the other leads to the same value for the spread between the lines.
- Although done rarely, one can report the direct results of trigonometric functions, such as the sine of the angle.
Remove ads
Angles between curves

The angle between a line and a curve (mixed angle) or between two intersecting curves (curvilinear angle) is defined to be the angle between the tangents at the point of intersection. Various names (now rarely, if ever, used) have been given to particular cases:—amphicyrtic (Gr. ἀμφί, on both sides, κυρτός, convex) or cissoidal (Gr. κισσός, ivy), biconvex; xystroidal or sistroidal (Gr. ξυστρίς, a tool for scraping), concavo-convex; amphicoelic (Gr. κοίλη, a hollow) or angulus lunularis, biconcave.[52]
Remove ads
Bisecting and trisecting angles
The ancient Greek mathematicians knew how to bisect an angle (divide it into two angles of equal measure) using only a compass and straightedge but could only trisect certain angles. In 1837, Pierre Wantzel showed that this construction could not be performed for most angles.
Dot product and generalisations
Summarize
Perspective
In the Euclidean space, the angle θ between two Euclidean vectors u and v is related to their dot product and their lengths by the formula
This formula supplies an easy method to find the angle between two planes (or curved surfaces) from their normal vectors and between skew lines from their vector equations.
Inner product
To define angles in an abstract real inner product space, we replace the Euclidean dot product ( · ) by the inner product , i.e.
In a complex inner product space, the expression for the cosine above may give non-real values, so it is replaced with or, more commonly, using the absolute value, with
The latter definition ignores the direction of the vectors. It thus describes the angle between one-dimensional subspaces and spanned by the vectors and correspondingly.
Angles between subspaces
The definition of the angle between one-dimensional subspaces and given by in a Hilbert space can be extended to subspaces of finite number of dimensions. Given two subspaces , with , this leads to a definition of angles called canonical or principal angles between subspaces.
Angles in Riemannian geometry
In Riemannian geometry, the metric tensor is used to define the angle between two tangents. Where U and V are tangent vectors and gij are the components of the metric tensor G,
Hyperbolic angle

A hyperbolic angle is an argument of a hyperbolic function just as the circular angle is the argument of a circular function. The comparison can be visualized as the size of the openings of a hyperbolic sector and a circular sector since the areas of these sectors correspond to the angle magnitudes in each case.[53] Unlike the circular angle, the hyperbolic angle is unbounded. When the circular and hyperbolic functions are viewed as infinite series in their angle argument, the circular ones are just alternating series forms of the hyperbolic functions. This comparison of the two series corresponding to functions of angles was described by Leonhard Euler in Introduction to the Analysis of the Infinite (1748).
Remove ads
History and etymology
Summarize
Perspective
The word angle comes from the Latin word angulus, meaning "corner". Cognate words include the Greek ἀγκύλος (ankylοs) meaning "crooked, curved" and the English word "ankle". Both are connected with the Proto-Indo-European root *ank-, meaning "to bend" or "bow".[54]
Philosophers have debated the nature of angles for millennia, with some arguing that angles are a measure (quantity), and others saying they are a kind of shape defined by the lines that bound it (qualitative relation), and still others saying an angle is both.[55] Pedagogically, the accepted answer is that angles are defined as figures, and the measure of an angle is defined as the number of congruent non-overlapping copies of a unit angle necessary to cover the angle and its interior. Angles are said to be equal in measure and similar or congruent in shape.[56]
Euclid defines a plane angle as the inclination to each other, in a plane, of two lines that meet each other and do not lie straight with respect to each other. According to the Neoplatonic metaphysician Proclus, an angle must be either a quality, a quantity, or a relationship. The first concept, angle as quality, was used by Eudemus of Rhodes, who regarded an angle as a deviation from a straight line; the second, angle as quantity, by Carpus of Antioch, who regarded it as the interval or space between the intersecting lines; Euclid adopted the third: angle as a relationship.[57]
Vertical angle theorem
The equality of vertically opposite angles is called the vertical angle theorem. Eudemus of Rhodes attributed the proof to Thales of Miletus.[58][23] The proposition showed that since both of a pair of vertical angles are supplementary to both of the adjacent angles, the vertical angles are equal in measure. According to a historical note,[23] when Thales visited Egypt, he observed that whenever the Egyptians drew two intersecting lines, they would measure the vertical angles to make sure that they were equal. Thales concluded that one could prove that all vertical angles are equal if one accepted some general notions such as:
- All straight angles are equal.
- Equals added to equals are equal.
- Equals subtracted from equals are equal.
When two adjacent angles form a straight line, they are supplementary. Therefore, if we assume that the measure of angle A equals x, the measure of angle C would be 180° − x. Similarly, the measure of angle D would be 180° − x. Both angle C and angle D have measures equal to 180° − x and are congruent. Since angle B is supplementary to both angles C and D, either of these angle measures may be used to determine the measure of Angle B. Using the measure of either angle C or angle D, we find the measure of angle B to be 180° − (180° − x) = x. Therefore, both angle A and angle B have measures equal to x and are equal in measure.
Remove ads
Angles in geography and astronomy
Summarize
Perspective
In geography, the location of any point on the Earth can be identified using a geographic coordinate system. This system specifies the latitude and longitude of any location in terms of angles subtended at the center of the Earth, using the equator and (usually) the Greenwich meridian as references.
In astronomy, a given point on the celestial sphere (that is, the apparent position of an astronomical object) can be identified using any of several astronomical coordinate systems, where the references vary according to the particular system. Astronomers measure the angular separation of two stars by imagining two lines through the center of the Earth, each intersecting one of the stars. The angle between those lines and the angular separation between the two stars can be measured.
In both geography and astronomy, a sighting direction can be specified in terms of a vertical angle such as altitude angle or elevation with respect to the horizon as well as the azimuth with respect to north.
Astronomers also measure objects' apparent size as an angular diameter. For example, the full moon has an angular diameter of approximately 0.5°, or 30 arcminutes, when viewed from Earth. One could say, "The Moon's diameter subtends an angle of half a degree." The small-angle formula can convert such an angular measurement into a distance/size ratio.
Other astronomical approximations include:
- 0.5° is the approximate angular diameter of the Sun and of the Moon as viewed from Earth.
- 1° is the approximate angular width of the little finger at arm's length.
- 10° is the approximate angular width of a closed fist at arm's length.
- 20° is the approximate angular width of a handspan at arm's length.
These measurements depend on the individual subject, and the above should be treated as rough rule of thumb approximations only.
In astronomy, right ascension is usually measured in angular units that are expressed in terms of time based on a 24-hour day.[59]
Remove ads
See also
- Angle measuring instrument
- Angles between flats
- Angular statistics (mean, standard deviation)
- Angle bisector
- Angular acceleration
- Angular diameter
- Angular velocity
- Argument (complex analysis)
- Astrological aspect
- Central angle
- Clock angle problem
- Decimal degrees
- Dihedral angle
- Exterior angle theorem
- Golden angle
- Great circle distance
- Horn angle
- Inscribed angle
- Irrational angle
- Phase (waves)
- Protractor
- Solid angle
- Spherical angle
- Subtended angle
- Tangential angle
- Transcendent angle
- Trisection
- Zenith angle
Notes
- This approach requires, however, an additional proof that the measure of the angle does not change with changing radius r, in addition to the issue of "measurement units chosen". A smoother approach is to measure the angle by the length of the corresponding unit circle arc. Here "unit" can be chosen to be dimensionless in the sense that it is the real number 1 associated with the unit segment on the real line. See Dimitrić (2012), for instance.
- An angular sector can be constructed by the combination of two rotated half-planes, either their intersection or union (in the case of acute or obtuse angles, respectively).[9][10] It corresponds to a circular sector of infinite radius and a flat pencil of half-lines.[11]
Remove ads
References
Bibliography
Further reading
External links
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads

































