Omnitruncated 7-simplex honeycomb

In seven-dimensional Euclidean geometry, the omnitruncated 7-simplex honeycomb is a space-filling tessellation (or honeycomb). It is composed entirely of omnitruncated 7-simplex facets.

Omnitruncated 7-simplex honeycomb
(No image)
Type	Uniform honeycomb
Family	Omnitruncated simplectic honeycomb
Schläfli symbol	{3[8]}
Coxeter–Dynkin diagrams
6-face types	t0123456{3,3,3,3,3,3}
Vertex figure	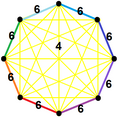Irr. 7-simplex
Symmetry	${\displaystyle {\tilde {A}}_{8}}$×16, [8[3[8]]]
Properties	vertex-transitive

The facets of all omnitruncated simplectic honeycombs are called permutahedra and can be positioned in n+1 space with integral coordinates, permutations of the whole numbers (0,1,..,n).

A7* lattice

The A^*
₇ lattice (also called A⁸
₇) is the union of eight A₇ lattices, and has the vertex arrangement to the dual honeycomb of the omnitruncated 7-simplex honeycomb, and therefore the Voronoi cell of this lattice is an omnitruncated 7-simplex.

∪ ∪ ∪ ∪ ∪ ∪ ∪ = dual of .

Related polytopes and honeycombs

This honeycomb is one of 29 unique uniform honeycombs^[1] constructed by the ${\displaystyle {\tilde {A}}_{7}}$ Coxeter group, grouped by their extended symmetry of rings within the regular octagon diagram:

A7 honeycombs
Octagon symmetry	Extended symmetry	Extended diagram	Extended group	Honeycombs
a1	[3[8]]		${\displaystyle {\tilde {A}}_{7}}$
d2	<[3[8]]>		${\displaystyle {\tilde {A}}_{7}}$×21	1
p2	[[3[8]]]		${\displaystyle {\tilde {A}}_{7}}$×22	2
d4	<2[3[8]]>		${\displaystyle {\tilde {A}}_{7}}$×41
p4	[2[3[8]]]		${\displaystyle {\tilde {A}}_{7}}$×42
d8	[4[3[8]]]		${\displaystyle {\tilde {A}}_{7}}$×8
r16	[8[3[8]]]		${\displaystyle {\tilde {A}}_{7}}$×16	3

See also

Regular and uniform honeycombs in 7-space:

• 7-cubic honeycomb
• 7-demicubic honeycomb
• 7-simplex honeycomb
• Truncated 7-simplex honeycomb
• 3₃₁ honeycomb