Pursuit curve

In geometry, a curve of pursuit is a curve constructed by analogy to having a point or points representing pursuers and pursued; the curve of pursuit is the curve traced by the pursuers.

A simple pursuit curve in which P is the pursuer and A is the pursued

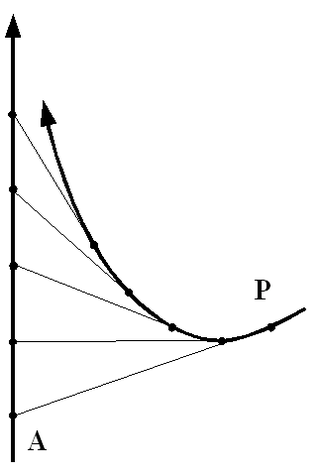
Definition

With the paths of the pursuer and pursued parameterized in time, the pursued is always on the pursuer's tangent. That is, given F(t), the pursuer (follower), and L(t), the pursued (leader), for every t with F′(t) ≠ 0 there is an x such that

${\displaystyle L(t)=F(t)+xF'\!(t).}$

History

Pierre Bouguer's 1732 article studying pursuit curves

The pursuit curve was first studied by Pierre Bouguer in 1732. In an article on navigation, Bouguer defined a curve of pursuit to explore the way in which one ship might maneuver while pursuing another.^[1]

Leonardo da Vinci has occasionally been credited with first exploring curves of pursuit. However Paul J. Nahin, having traced such accounts as far back as the late 19th century, indicates that these anecdotes are unfounded.^[2]

Single pursuer

Curves of pursuit with different parameters

The path followed by a single pursuer, following a pursued that moves at constant speed on a line, is a radiodrome.

It is a solution of the differential equation 1 +  y′ ² = k² (a − x)² y′′ ², where k is the ratio in speed of the pursued over the pursuer. The special case with k = 1/2 is the Tschirnhausen cubic.

Multiple pursuers

Curve of pursuit of vertices of a square (the mice problem for n=4).

Typical drawings of curves of pursuit have each point acting as both pursuer and pursued, inside a polygon, and having each pursuer pursue the adjacent point on the polygon. An example of this is the mice problem, in which pursuers on the vertices of a regular polygon chase each other along logarithmic spirals.

See also

• Tractrix
• Circles of Apollonius#Apollonius pursuit problem
• Pursuit–evasion