Radiodrome

In geometry, a radiodrome is a specific type of pursuit curve: the path traced by a point that continuously moves toward a target traveling in a straight line at constant speed. The term comes from the Latin radius (ray or spoke) and the Greek dromos (running or racetrack), reflecting the radial nature of the motion.

The path of a dog chasing a hare running along a vertical straight line at a constant speed. The dog runs towards the momentary position of the hare, and will be changing his heading continuously.

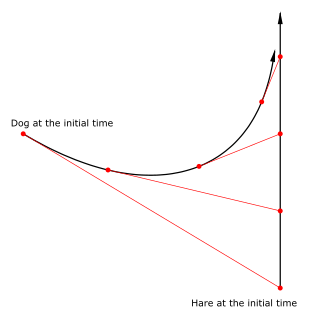
The most classic and widely recognized example is the so-called dog curve, which describes the path of a dog swimming across a river toward a hare moving along the opposite bank. Because of the current, the dog must constantly adjust its heading, resulting in a longer, curved trajectory. This case was first described by the French mathematician and hydrographer Pierre Bouguer in 1732.

Radiodromes are distinguished from other pursuit curves by the assumption that the pursuer always heads directly toward the target’s current position, while the target moves at a constant velocity along a straight path.

Mathematical analysis

Introduce a coordinate system with origin at the position of the dog at time zero and with y-axis in the direction the hare is running with the constant speed V_t. The position of the hare at time zero is (A_x, A_y) with A_x > 0 and at time t it is

${\displaystyle (T_{x}\ ,\ T_{y})\ =\ (A_{x}\ ,\ A_{y}+V_{t}t)~.}$

1

The dog runs with the constant speed V_d towards the instantaneous position of the hare.

The differential equation corresponding to the movement of the dog, (x(t), y(t)), is consequently

${\displaystyle {\dot {x}}=V_{d}\ {\frac {T_{x}-x}{\sqrt {(T_{x}-x)^{2}+(T_{y}-y)^{2}}}}}$

2

${\displaystyle {\dot {y}}=V_{d}\ {\frac {T_{y}-y}{\sqrt {(T_{x}-x)^{2}+(T_{y}-y)^{2}}}}~.}$

3

It is possible to obtain a closed-form analytic expression y=f(x) for the motion of the dog. From (2) and (3), it follows that

${\displaystyle y'(x)={\frac {T_{y}-y}{T_{x}-x}}}$ .

4

Multiplying both sides with ${\displaystyle T_{x}-x}$ and taking the derivative with respect to x, using that

${\displaystyle {\frac {dT_{y}}{dx}}\ =\ {\frac {dT_{y}}{dt}}\ {\frac {dt}{dx}}\ =\ {\frac {V_{t}}{V_{d}}}\ {\sqrt {{y'}^{2}+1}}~,}$

5

one gets

${\displaystyle y''={\frac {V_{t}\ {\sqrt {1+{y'}^{2}}}}{V_{d}(A_{x}-x)}}}$

6

or

${\displaystyle {\frac {y''}{\sqrt {1+{y'}^{2}}}}={\frac {V_{t}}{V_{d}(A_{x}-x)}}~.}$

7

From this relation, it follows that

${\displaystyle \sinh ^{-1}(y')=B-{\frac {V_{t}}{V_{d}}}\ \ln(A_{x}-x)~,}$

8

where B is the constant of integration determined by the initial value of y' at time zero, y' (0)= sinh(B − (V_t /V_d) lnA_x), i.e.,

${\displaystyle B={\frac {V_{t}}{V_{d}}}\ \ln(A_{x})+\ln \left(y'(0)+{\sqrt {{y'(0)}^{2}+1}}\right).}$

9

From (8) and (9), it follows after some computation that

${\displaystyle y'={\frac {1}{2}}\left[\left(y'(0)+{\sqrt {{y'(0)}^{2}+1}}\right)\left(1-{\frac {x}{A_{x}}}\right)^{-{\frac {V_{t}}{V_{d}}}}+\left(y'(0)-{\sqrt {{y'(0)}^{2}+1}}\right)\left(1-{\frac {x}{A_{x}}}\right)^{\frac {V_{t}}{V_{d}}}\right]}$ .

10

Furthermore, since y(0)=0, it follows from (1) and (4) that

${\displaystyle y'(0)={\frac {A_{y}}{A_{x}}}}$ .

11

If, now, V_t ≠ V_d, relation (10) integrates to

${\displaystyle y=C-{\frac {A_{x}}{2}}\left[{\frac {\left(y'(0)+{\sqrt {{y'(0)}^{2}+1}}\right)\left(1-{\frac {x}{A_{x}}}\right)^{1-{\frac {V_{t}}{V_{d}}}}}{1-{\frac {V_{t}}{V_{d}}}}}+{\frac {\left(y'(0)-{\sqrt {{y'(0)}^{2}+1}}\right)\left(1-{\frac {x}{A_{x}}}\right)^{1+{\frac {V_{t}}{V_{d}}}}}{1+{\frac {V_{t}}{V_{d}}}}}\right],}$

12

where C is the constant of integration. Since again y(0)=0, it's

${\displaystyle C={\frac {A_{x}}{2}}\left[{\frac {y'(0)+{\sqrt {{y'(0)}^{2}+1}}}{1-{\frac {V_{t}}{V_{d}}}}}+{\frac {y'(0)-{\sqrt {{y'(0)}^{2}+1}}}{1+{\frac {V_{t}}{V_{d}}}}}\right]}$.

13

The equations (11), (12) and (13), then, together imply

${\displaystyle y={\frac {1}{2}}\left\{{\frac {A_{y}+{\sqrt {A_{x}^{2}+A_{y}^{2}}}}{1-{\frac {V_{t}}{V_{d}}}}}\left[1-\left(1-{\frac {x}{A_{x}}}\right)^{1-{\frac {V_{t}}{V_{d}}}}\right]+{\frac {A_{y}-{\sqrt {A_{x}^{2}+A_{y}^{2}}}}{1+{\frac {V_{t}}{V_{d}}}}}\left[1-\left(1-{\frac {x}{A_{x}}}\right)^{1+{\frac {V_{t}}{V_{d}}}}\right]\right\}}$ .

14

If V_t = V_d, relation (10) gives, instead,

${\displaystyle y=C-{\frac {A_{x}}{2}}\left[\left(y'(0)+{\sqrt {{y'(0)}^{2}+1}}\right)\ln \left(1-{\frac {x}{A_{x}}}\right)+{\frac {1}{2}}\left(y'(0)-{\sqrt {{y'(0)}^{2}+1}}\right)\left(1-{\frac {x}{A_{x}}}\right)^{2}\right]}$ .

15

Using y(0)=0 once again, it follows that

${\displaystyle C={\frac {A_{x}}{4}}\left(y'(0)-{\sqrt {{y'(0)}^{2}+1}}\right).}$

16

The equations (11), (15) and (16), then, together imply that

${\displaystyle y={\frac {1}{4}}\left(A_{y}-{\sqrt {A_{x}^{2}+A_{y}^{2}}}\right)\left[1-\left(1-{\frac {x}{A_{x}}}\right)^{2}\right]-{\frac {1}{2}}\left(A_{y}+{\sqrt {A_{x}^{2}+A_{y}^{2}}}\right)\ln \left(1-{\frac {x}{A_{x}}}\right)}$ .

17

If V_t < V_d, it follows from (14) that

${\displaystyle \lim _{x\to A_{x}}y(x)={\frac {1}{2}}\left({\frac {A_{y}+{\sqrt {A_{x}^{2}+A_{y}^{2}}}}{1-{\frac {V_{t}}{V_{d}}}}}+{\frac {A_{y}-{\sqrt {A_{x}^{2}+A_{y}^{2}}}}{1+{\frac {V_{t}}{V_{d}}}}}\right).}$

18

If V_t ≥ V_d, one has from (14) and (17) that ${\displaystyle \lim _{x\to A_{x}}y(x)=\infty }$, which means that the hare will never be caught, whenever the chase starts.

See also

• Mice problem

References

• Nahin, Paul J. (2012), Chases and Escapes: The Mathematics of Pursuit and Evasion, Princeton: Princeton University Press, ISBN 978-0-691-12514-5.
• Gomes Teixera, Francisco (1909), Imprensa da universidade (ed.), Traité des Courbes Spéciales Remarquables, vol. 2, Coimbra, p. 255{{citation}}: CS1 maint: location missing publisher (link)