Quarter 5-cubic honeycomb

In five-dimensional Euclidean geometry, the quarter 5-cubic honeycomb is a uniform space-filling tessellation (or honeycomb). It has half the vertices of the 5-demicubic honeycomb, and a quarter of the vertices of a 5-cube honeycomb.^[1] Its facets are 5-demicubes and runcinated 5-demicubes.

quarter 5-cubic honeycomb
(No image)
Type	Uniform 5-honeycomb
Family	Quarter hypercubic honeycomb
Schläfli symbol	q{4,3,3,3,4}
Coxeter-Dynkin diagram	=
5-face type	h{4,33}, h4{4,33},
Vertex figure	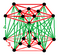Rectified 5-cell antiprism or Stretched birectified 5-simplex
Coxeter group	${\displaystyle {\tilde {D}}_{5}}$×2 = [[31,1,3,31,1]]
Dual
Properties	vertex-transitive

Related honeycombs

This honeycomb is one of 20 uniform honeycombs constructed by the ${\displaystyle {\tilde {D}}_{5}}$ Coxeter group, all but 3 repeated in other families by extended symmetry, seen in the graph symmetry of rings in the Coxeter–Dynkin diagrams. The 20 permutations are listed with its highest extended symmetry relation:

D5 honeycombs
Extended symmetry	Extended diagram	Extended group	Honeycombs
[31,1,3,31,1]		${\displaystyle {\tilde {D}}_{5}}$
<[31,1,3,31,1]> ↔ [31,1,3,3,4]	↔	${\displaystyle {\tilde {D}}_{5}}$×21 = ${\displaystyle {\tilde {B}}_{5}}$	, , , , , ,
[[31,1,3,31,1]]		${\displaystyle {\tilde {D}}_{5}}$×22	,
<2[31,1,3,31,1]> ↔ [4,3,3,3,4]	↔	${\displaystyle {\tilde {D}}_{5}}$×41 = ${\displaystyle {\tilde {C}}_{5}}$	, , , , ,
[<2[31,1,3,31,1]>] ↔ [[4,3,3,3,4]]	↔	${\displaystyle {\tilde {D}}_{5}}$×8 = ${\displaystyle {\tilde {C}}_{5}}$×2	, ,

See also

Regular and uniform honeycombs in 5-space:

• 5-cube honeycomb
• 5-demicube honeycomb
• 5-simplex honeycomb
• Truncated 5-simplex honeycomb
• Omnitruncated 5-simplex honeycomb