Top Qs
Timeline
Chat
Perspective
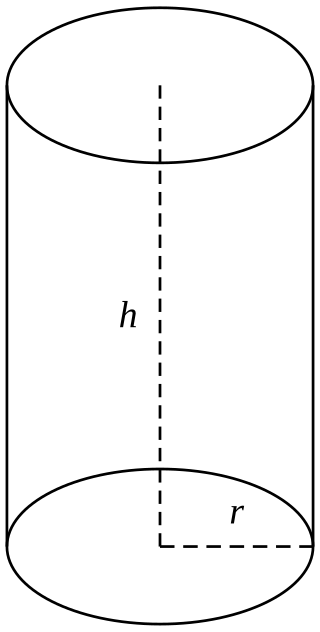
Right circular cylinder
Cylinder whose generatrices are perpendicular to the bases From Wikipedia, the free encyclopedia
Remove ads
A right circular cylinder is a cylinder whose generatrices are perpendicular to the bases. Thus, in a right circular cylinder, the generatrix and the height have the same measurements.[1] It is also less often called a cylinder of revolution, because it can be obtained by rotating a rectangle of sides and around one of its sides. Fixing as the side on which the revolution takes place, we obtain that the side , perpendicular to , will be the measure of the radius of the cylinder.[2]

In addition to the right circular cylinder, within the study of spatial geometry there is also the oblique circular cylinder, characterized by not having the generatrices perpendicular to the bases.[3]
Remove ads
Elements of the right circular cylinder
Bases: the two parallel and congruent circles of the bases;[4]
Axis: the line determined by the two points of the centers of the cylinder's bases;[1]
Height: the distance between the two planes of the cylinder's bases;[2]
Generatrices: the line segments parallel to the axis and that have ends at the points of the bases' circles.[2]
Lateral and total areas
Summarize
Perspective

The lateral surface of a right cylinder is the meeting of the generatrices.[3] It can be obtained by the product between the length of the circumference of the base and the height of the cylinder. Therefore, the lateral surface area is given by:
- .[2]
Where:
- represents the lateral surface area of the cylinder;
- is approximately 3.14159;
- is the distance between the lateral surface of the cylinder and the axis, i.e. it is the value of the radius of the base;
- is the height of the cylinder;
- is the length of the circumference of the base, since , that is, .[5]
Note that in the case of the right circular cylinder, the height and the generatrix have the same measure, so the lateral area can also be given by:
- .
The area of the base of a cylinder is the area of a circle (in this case, we define that the circle has a radius with measure ):
- .
To calculate the total area of a right circular cylinder, you simply add the lateral area to the area of the two bases:
- .
Replacing and , we have:
or even
- .
Remove ads
Volume
Summarize
Perspective

Cavalieri's principle states that if two solids of the same height and congruent base areas, are positioned on the same plane, such that any other plane parallel to this plane sections both solids, determining from this section two polygons with the same area,[6] then the volume of the two solids will be the same. One can use Cavalieri's principle to determine the volume of the cylinder.
This is because the volume of a cylinder can be obtained in the same way as the volume of a prism with the same height and the same area of the base. Therefore, simply multiply the area of the base by the height:
- .
Since the area of a circle of radius , which is the base of the cylinder, is given by it follows that:
or even
- .
Equation in Cartesian analytic geometry
Summarize
Perspective
The traditional representation of right circular cylinders in 3D analytic geometry uses the equation
with
where is the radius of the circular base and is the height of the cylinder. However, this representation has a noticeable limitation in that the end caps of the cylinder are missing. In some applications, it is desirable to include the end caps. Moreover, this equation for the cylinder is disingenuous in three dimensions because the variable is disjoint from the main equation. In and of itself, this equation is quasi-3D.
Meanwhile, it is possible to represent the cylinder with end caps by using the Fernandez-Guasti squircle.[7] The cylinder can be represented by the equation
with
This equation provides a genuine 3D representation of the cylinder with end caps. Furthermore, this algebraic equation is a low degree quartic. This quartic surface can be visualized using online graphing calculators such as Desmos.[8]
Remove ads
Equilateral cylinder
Summarize
Perspective

The equilateral cylinder is characterized by being a right circular cylinder in which the diameter of the base is equal to the value of the height (generatrix).[4]
Then, assuming that the radius of the base of an equilateral cylinder is then the diameter of the base of this cylinder is and its height is .[4]
Its lateral area can be obtained by replacing the height value by :
- .
The result can be obtained in a similar way for the total area:
- .
For the equilateral cylinder it is possible to obtain a simpler formula to calculate the volume. Simply substitute the radius and height measurements defined earlier into the volume formula for a straight circular cylinder:
Remove ads
Meridian section
It is the intersection between a plane containing the axis of the cylinder and the cylinder.[4]
In the case of the right circular cylinder, the meridian section is a rectangle, because the generatrix is perpendicular to the base. The equilateral cylinder, on the other hand, has a square meridian section because its height is congruent to the diameter of the base.[1][4]
Examples of objects with a right circular cylinder shape
- Bale of straw
- Titanium cylinder
- Candle
See also
References
Bibliography
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads