Siamese method

Publication

De la Loubère published his findings in his book A new historical relation of the kingdom of Siam (Du Royaume de Siam, 1693), under the chapter entitled The problem of the magical square according to the Indians.^[5] Although the method is generally qualified as "Siamese", which refers to de la Loubère's travel to the country of Siam, de la Loubère himself learnt it from a Frenchman named M.Vincent (a doctor, who had first travelled to Persia and then to Siam, and was returning to France with the de la Loubère embassy), who himself had learnt it in the city of Surat in India:^[5]

"Mr. Vincent, whom I have so often mentioned in my Relations, seeing me one day in the ship, during our return, studiously to range the Magical Squares after the method of Bachet, informed me that the Indians of Suratte ranged them with much more facility, and taught me their method for the unequal squares only, having, he said, forgot that of the equal"
— Simon de la Loubère, A new historical relation of the kingdom of Siam.^[5]

The method

Summarize

Perspective

The method was surprising in its effectiveness and simplicity:

"I hope that it will not be unacceptable that I give the rules and the demonstration of this method, which is surprising for its extreme facility to execute a thing, which has appeared difficult to our Mathematicians"
— Simon de la Loubère, A new historical relation of the kingdom of Siam.^[5]

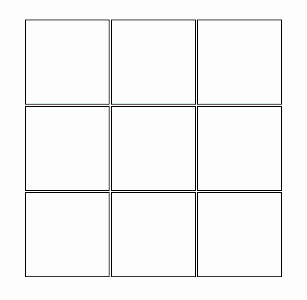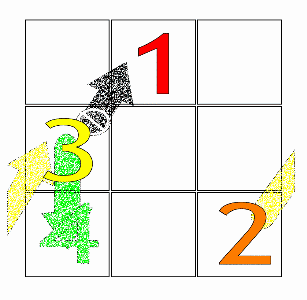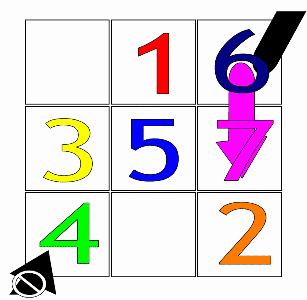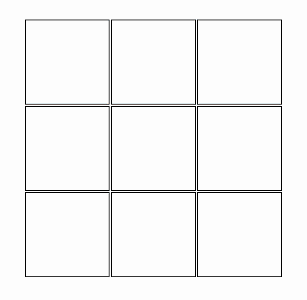
First, an arithmetic progression has to be chosen (such as the simple progression 1,2,3,4,5,6,7,8,9 for a square with three rows and columns (the Lo Shu square)).

Then, starting from the central box of the first row with the number 1 (or the first number of any arithmetic progression), the fundamental movement for filling the boxes is diagonally up and right (↗), one step at a time. When a move would leave the square, it is wrapped around to the last row or first column, respectively.

If a filled box is encountered, one moves vertically down one box (↓) instead, then continuing as before.

Order-3 magic squares

More information step 1, step 2 ...

step 1
	1
	.
	.

step 2
	1
	.
		2

step 3
	1
3
		2

step 4
	1
3
4		2

More information step 5, step 6 ...

step 5
	1
3	5
4		2

step 6
	1	6
3	5
4		2

step 7
	1	6
3	5	7
4		2

step 8
8	1	6
3	5	7
4		2

step 9
8	1	6
3	5	7
4	9	2

Order-5 magic squares

More information Step 1, Step 2 ...

Step 1
		1
		.
		.
		.
		.


1
.
.
.		3
.	2

Step 3
		1
	5
4		.
				3
			2

More information Step 4, Step 5 ...

Step 4
		1	8
	5	7
4	6	.
				3
			2

Step 5
		1	8	15
	5	7	14
4	6	13
10	12			3
11			2	9

Step 6
17	24	1	8	15
23	5	7	14	16
4	6	13	20	22
10	12	19	21	3
11	18	25	2	9

Other sizes

Any n-odd square ("odd-order square") can be thus built into a magic square. The Siamese method does not work however for n-even squares ("even-order squares", such as 2 rows/ 2 columns, 4 rows/ 4 columns etc...).

More information Order 3, Order 5 ...

Order 3
8	1	6
3	5	7
4	9	2

Order 5
17	24	1	8	15
23	5	7	14	16
4	6	13	20	22
10	12	19	21	3
11	18	25	2	9

Order 9
47	58	69	80	1	12	23	34	45
57	68	79	9	11	22	33	44	46
67	78	8	10	21	32	43	54	56
77	7	18	20	31	42	53	55	66
6	17	19	30	41	52	63	65	76
16	27	29	40	51	62	64	75	5
26	28	39	50	61	72	74	4	15
36	38	49	60	71	73	3	14	25
37	48	59	70	81	2	13	24	35

Other values

Any sequence of numbers can be used, provided they form an arithmetic progression (i.e. the difference of any two successive members of the sequence is a constant). Also, any starting number is possible. For example the following sequence can be used to form an order 3 magic square according to the Siamese method (9 boxes): 5, 10, 15, 20, 25, 30, 35, 40, 45 (the magic sum gives 75, for all rows, columns and diagonals). The magic sum in these cases will be the sum of the arithmetic progression used divided by the order of the magic square.

More information Order 3 ...

Order 3
40	5	30
15	25	35
20	45	10

Other starting points

It is possible not to start the arithmetic progression from the middle of the top row, but then only the row and column sums will be identical and result in a magic sum, whereas the diagonal sums will differ. The result will thus not be a true magic square:

More information Order 3 ...

Order 3
500	700	300
900	200	400
100	600	800

Rotations and reflections

Numerous other magic squares can be deduced from the above by simple rotations and reflections.

Variations

Summarize

Perspective

A slightly more complicated variation of this method exists in which the first number is placed in the box just above the center box. The fundamental movement for filling the boxes remains up and right (↗), one step at a time. However, if a filled box is encountered, one moves vertically up two boxes instead, then continuing as before.

More information Order 5 ...

Order 5
23	6	19	2	15
10	18	1	14	22
17	5	13	21	9
4	12	25	8	16
11	24	7	20	3

Numerous variants can be obtained by simple rotations and reflections. The next square is equivalent to the above (a simple reflexion): the first number is placed in the box just below the center box. The fundamental movement for filling the boxes then becomes diagonally down and right (↘), one step at a time. If a filled box is encountered, one moves vertically down two boxes instead, then continuing as before.^[6]