Slash distribution

In probability theory, the slash distribution is the probability distribution of a standard normal variate divided by an independent standard uniform variate.^[1] In other words, if the random variable Z has a normal distribution with zero mean and unit variance, the random variable U has a uniform distribution on [0,1] and Z and U are statistically independent, then the random variable X = Z / U has a slash distribution. The slash distribution is an example of a ratio distribution. The distribution was named by William H. Rogers and John Tukey in a paper published in 1972.^[2]

Slash

Probability density function
Cumulative distribution function
Parameters	none
Support	${\displaystyle x\in (-\infty ,\infty )}$
PDF	${\displaystyle {\begin{cases}{\frac {\varphi (0)-\varphi (x)}{x^{2}}}&x\neq 0\\{\frac {1}{2{\sqrt {2\pi }}}}&x=0\\\end{cases}}}$
CDF	${\displaystyle {\begin{cases}\Phi (x)-\left[\varphi (0)-\varphi (x)\right]/x&x\neq 0\\1/2&x=0\\\end{cases}}}$
Mean	Does not exist
Median	0
Mode	0
Variance	Does not exist
Skewness	Does not exist
Excess kurtosis	Does not exist
MGF	Does not exist
CF	${\displaystyle {\sqrt {2\pi }}{\Big (}\varphi (t)+t\Phi (t)-\max\{t,0\}{\Big )}}$

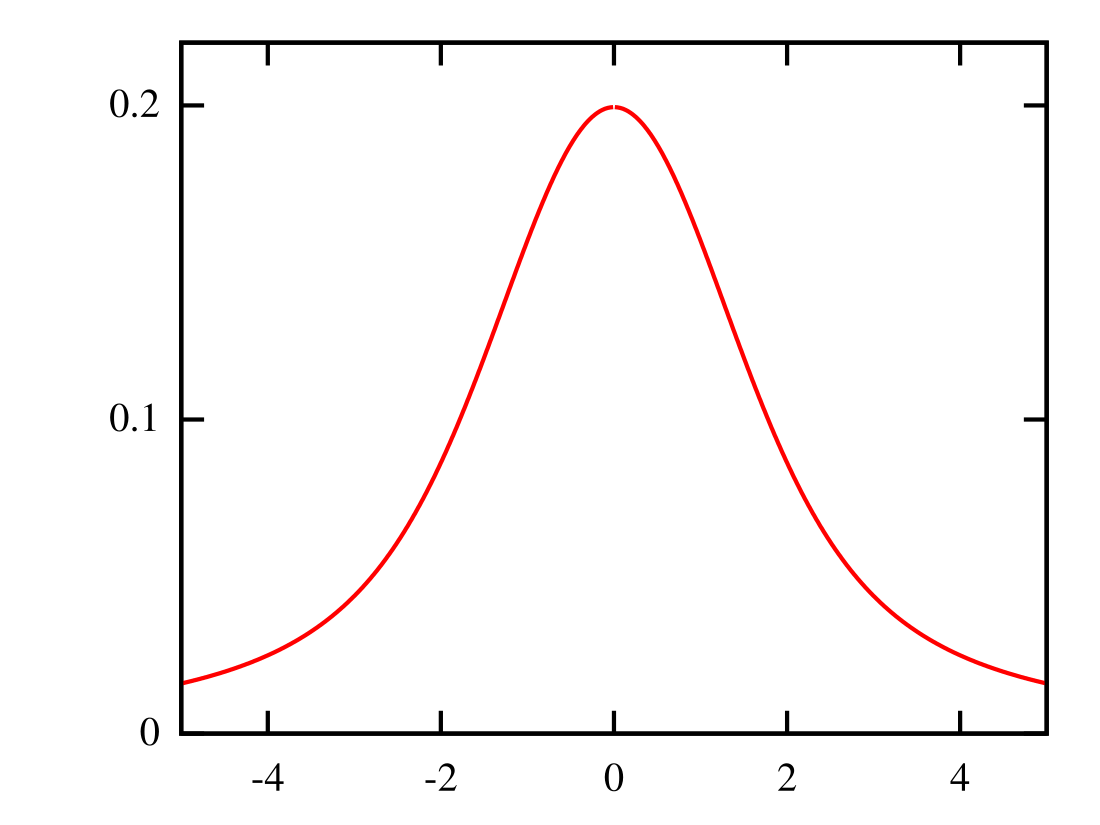
The probability density function (pdf) is

${\displaystyle f(x)={\frac {\varphi (0)-\varphi (x)}{x^{2}}}.}$

where ${\displaystyle \varphi (x)}$ is the probability density function of the standard normal distribution.^[3] The quotient is undefined at x = 0, but the discontinuity is removable:

${\displaystyle \lim _{x\to 0}f(x)={\frac {\varphi (0)}{2}}={\frac {1}{2{\sqrt {2\pi }}}}}$

The most common use of the slash distribution is in simulation studies. It is a useful distribution in this context because it has heavier tails than a normal distribution, but it is not as pathological as the Cauchy distribution.^[3]

See also

• Scale mixture