Straightedge-only construction

In geometry, a Steiner construction – also known as straightedge-only construction^[1] – is the construction of lengths, angles, and other geometric figures using only an idealized ruler. It is similar to compass and straightedge constructions except the compass is not available for the construction.

The idealized ruler, known as a straightedge, is assumed to be infinite in length, have only one edge, and no markings on it. It can be used to draw a line between any two marked points on a plane and construct the intersection points between any two lines.

The straightedge is strictly weaker than a straightedge and compass together; a straightedge can only produce projective invariants of the initial configuration. For example, one cannot mark the midpoint of a segment using a straightedge alone, since a projective transformation can send the midpoint elsewhere. This is in contrast to the Mohr–Mascheroni theorem, which states that every straightedge and compass construction can be made with just a compass alone.

A set of points or lines is said to be Steiner-constructible if it can be constructed using only a straightedge. Compare this with the term constructible, which includes constructions involving a compass.

It turns out, if a given single circle and its center is initially given, every straightedge and compass construction becomes possible using a straightedge alone, making it just as powerful as a compass. This result is known as the Poncelet–Steiner theorem.

History

The term Steiner construction is named after Jakob Steiner, who first proved the Poncelet–Steiner theorem in 1833, an important theorem about straightedge-only constructions. Since then, the term is used to refer to geometric constructions which only involve the straightedge.^[1]

Constructions

In the book The Ruler In Geometrical Constructions (1961), A. S. Smogorzhevskii provides multiple constructions that are possible using only a straightedge. The book also contains elementary proofs for these constructions.^[2]

Harmonic conjugate

Given three points A, B, C on a straight line, the harmonic conjugate D of point C with respect to A and B can be constructed. This is done by taking advantage of Ceva's theorem and Menelaus's theorem.

As a corollary, if there are two points A and B with their midpoint M given, one can construct a line parallel to line AB passing through any given points. The converse is also true.

The dual version is as follows: Given three lines a, b, c all passing through a common point, one can construct the line d which, together with line c, divide lines a and b harmonically.

Pole and polar

Given a conic section q and a point P not on the conic section, it is possible to construct the polar line π of point P. Conversely, if a straight line π is given, it is possible to construct its pole P on the conic section.

Tangent to a conic

Given a conic section q and a point P, it is possible to construct tangents to q through point P. This construction is possible regardless of whether P is on the conic section or not.

Smogorzhevskii (2021) provides an elementary construction of this result in their book, but it is also possible give a proof for the circle case using analytical geometry and trigonometry.^[3]

Determining whether six points lie on a conic

Given 6 points A, B, C, D, E, F, it can be determined using only a straightedge whether they all lie on the same conic section.

The dual version is as follows: Given any 6 lines a, b, c, d, e, f, it can be determined whether they inscribe a single conic section.

Blaise Pascal proved the first one in 1639 by making use of Pascal's theorem, which reduces testing whether six points lie on a conic to checking whether three points are collinear. The dual version may be proved using Brianchon's theorem.^[4]

In 2021, Traves and Wehlau found a straightedge-only method to check whether 10 points lie on the same cubic curve.^[4]

Constructions with two given parallel lines

If two parallel lines l and m are initially given, the following are possible:

• Bisect a given segment AB on line l.
• Draw a line passing through a given point P parallel to the given lines l and m.
• Given segment AB and point C on line l, construct segment CD on line l such that CD = n · AB (n is a whole number).
• Given segment AB on line l, divide AB into n equal parts (n is a whole number).

Constructions with a given parallelogram or square

If any parallelogram is initially given, the following is possible:

• Draw a line passing through a given point P and parallel to any given line l.

If any square is initially given, the following are possible:

• Draw a line passing through a given point P and perpendicular to any given line l. This construction works regardless of whether P is on line l or not.
• Bisect any given right angle.

Poncelet–Steiner theorem

Main article: Poncelet–Steiner theorem

Construction of a parallel (h) to a diameter g through any given point P, using only a straightedge and a given fixed circle

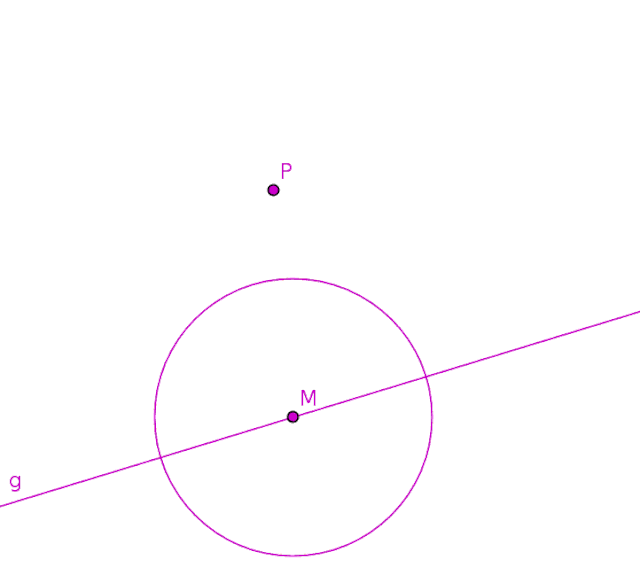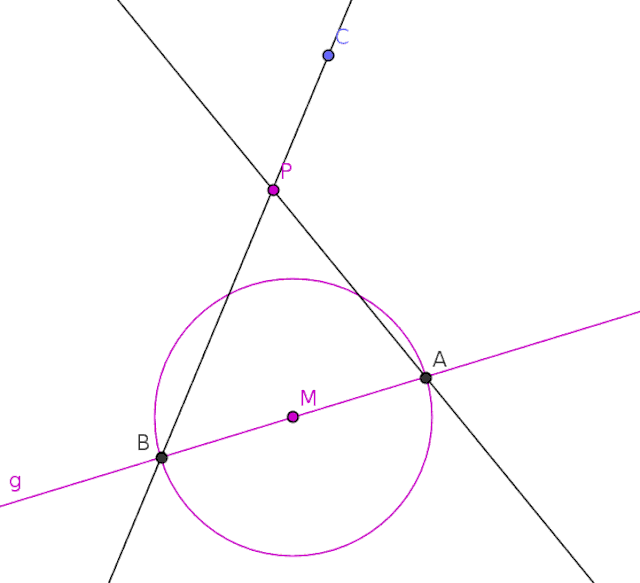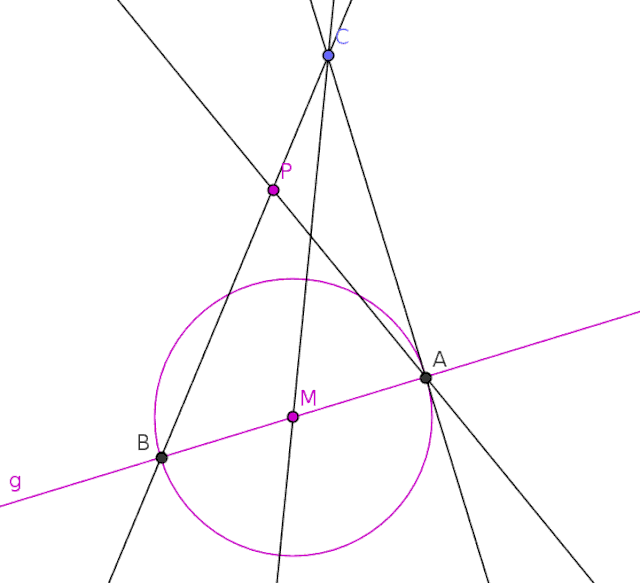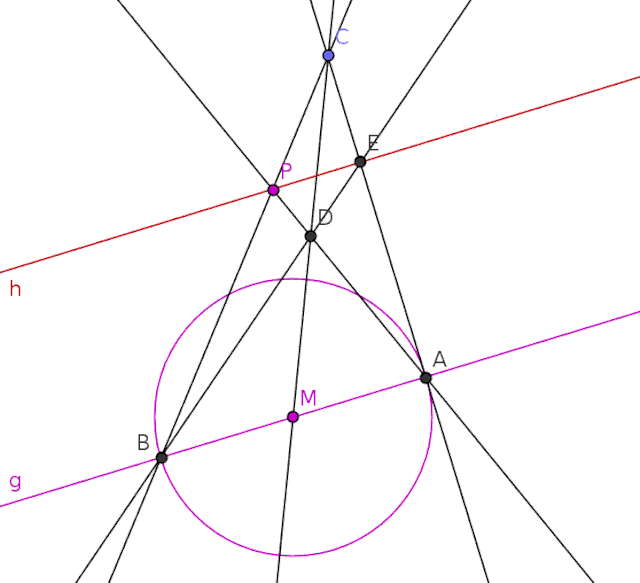
The Poncelet–Steiner theorem states that only a single circle and its center is needed for a straightedge to be able to perform any straightedge-and-compass construction. The theorem was first suggested by Jean Victor Poncelet in 1822 and proven by Jakob Steiner in 1833.

This shows that, while a compass can make constructions easier, it is no longer needed once the first circle has been drawn. All constructions thereafter can be performed using only the straightedge, although the arcs of circles themselves cannot be drawn without the compass.

Other variations of the theorem also give the same result, such as when two intersecting circles (without their centers) are given, or two concentric circles are given.

Limitations

The straightedge is strictly weaker than a straightedge and compass together. This is because a straightedge can only produce projective invariants of the initial configuration. Because lengths are not preserved under projective transformation, any geometric construction involving lengths is not possible using a straightedge alone.

For example, without any additional information, it is impossible to construct midpoints, because there is a projective transformation that sends the midpoint elsewhere. Similarly, parallel lines are impossible to construct with only a straightedge.

Another example is, given a circle on the plane, it is impossible to construct its center using a straightedge alone. This was first proven by David Hilbert by constructing a projective transformation of the plane to itself such that the given circle is fixed, but the center of the circle is not preserved.^[5] This also demonstrates the importance of the circle center in the Poncelet–Steiner theorem.

This shows that a straightedge can only achieve results that projective geometry allows, which is far fewer than the full set of straightedge-and-compass constructions described in Euclid's Elements.