1 22 polytope

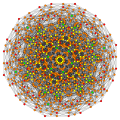
In 6-dimensional geometry, the 1₂₂ polytope is a uniform polytope, constructed from the E₆ group. It was first published in E. L. Elte's 1912 listing of semiregular polytopes, named as V₇₂ (for its 72 vertices).^[1]

122	Rectified 122	Birectified 122
221	Rectified 221
orthogonal projections in E6 Coxeter plane

Its Coxeter symbol is 1₂₂, describing its bifurcating Coxeter-Dynkin diagram, with a single ring on the end of the 1-node sequence. There are two rectifications of the 1₂₂, constructed by positions points on the elements of 1₂₂. The rectified 1₂₂ is constructed by points at the mid-edges of the 1₂₂. The birectified 1₂₂ is constructed by points at the triangle face centers of the 1₂₂.

These polytopes are from a family of 39 convex uniform polytopes in 6-dimensions, made of uniform polytope facets and vertex figures, defined by all permutations of rings in this Coxeter-Dynkin diagram: .

122 polytope

122 polytope
Type	Uniform 6-polytope
Family	1k2 polytope
Schläfli symbol	{3,32,2}
Coxeter symbol	122
Coxeter-Dynkin diagram	or
5-faces	54: 27 121 27 121
4-faces	702: 270 111 432 120
Cells	2160: 1080 110 1080 {3,3}
Faces	2160 {3}
Edges	720
Vertices	72
Vertex figure	Birectified 5-simplex: 022
Petrie polygon	Dodecagon
Coxeter group	E6, [[3,32,2]], order 103680
Properties	convex, isotopic

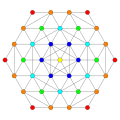
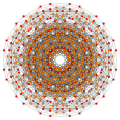
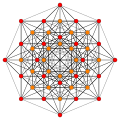
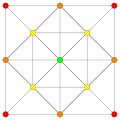
The 1₂₂ polytope contains 72 vertices, and 54 5-demicubic facets. It has a birectified 5-simplex vertex figure. Its 72 vertices represent the root vectors of the simple Lie group E₆.

Alternate names

• Pentacontatetra-peton (Acronym Mo) - 54-facetted polypeton (Jonathan Bowers)^[2]

Images

Coxeter plane orthographic projections

E6 [12]	D5 [8]	D4 / A2 [6]
(1,2)	(1,3)	(1,9,12)
B6 [12/2]	A5 [6]	A4 [[5]] = [10]	A3 / D3 [4]
(1,2)	(2,3,6)	(1,2)	(1,6,8,12)

Construction

It is created by a Wythoff construction upon a set of 6 hyperplane mirrors in 6-dimensional space.

The facet information can be extracted from its Coxeter-Dynkin diagram, .

Removing the node on either of 2-length branches leaves the 5-demicube, 1₃₁, .

The vertex figure is determined by removing the ringed node and ringing the neighboring node. This makes the birectified 5-simplex, 0₂₂, .

Seen in a configuration matrix, the element counts can be derived by mirror removal and ratios of Coxeter group orders.^[3]

E6		k-face	fk	f0	f1	f2	f3		f4			f5		k-figure	notes
A5		( )	f0	72	20	90	60	60	15	15	30	6	6	r{3,3,3}	E6/A5 = 72*6!/6! = 72
A2A2A1		{ }	f1	2	720	9	9	9	3	3	9	3	3	{3}×{3}	E6/A2A2A1 = 72*6!/3!/3!/2 = 720
A2A1A1		{3}	f2	3	3	2160	2	2	1	1	4	2	2	s{2,4}	E6/A2A1A1 = 72*6!/3!/2/2 = 2160
A3A1		{3,3}	f3	4	6	4	1080	*	1	0	2	2	1	{ }∨( )	E6/A3A1 = 72*6!/4!/2 = 1080
				4	6	4	*	1080	0	1	2	1	2
A4A1		{3,3,3}	f4	5	10	10	5	0	216	*	*	2	0	{ }	E6/A4A1 = 72*6!/5!/2 = 216
				5	10	10	0	5	*	216	*	0	2
D4		h{4,3,3}		8	24	32	8	8	*	*	270	1	1		E6/D4 = 72*6!/8/4! = 270
D5		h{4,3,3,3}	f5	16	80	160	80	40	16	0	10	27	*	( )	E6/D5 = 72*6!/16/5! = 27
				16	80	160	40	80	0	16	10	*	27

Related complex polyhedron

Orthographic projection in Aut(E6) Coxeter plane with 18-gonal symmetry for complex polyhedron, ₃{3}₃{4}₂. It has 72 vertices, 216 3-edges, and 54 3{3}3 faces.

The regular complex polyhedron ₃{3}₃{4}₂, , in ${\displaystyle \mathbb {C} ^{2}}$ has a real representation as the 1₂₂ polytope in 4-dimensional space. It has 72 vertices, 216 3-edges, and 54 3{3}3 faces. Its complex reflection group is ₃[3]₃[4]₂, order 1296. It has a half-symmetry quasiregular construction as , as a rectification of the Hessian polyhedron, .^[4]

Related polytopes and honeycomb

Along with the semiregular polytope, 2₂₁, it is also one of a family of 39 convex uniform polytopes in 6-dimensions, made of uniform polytope facets and vertex figures, defined by all permutations of rings in this Coxeter-Dynkin diagram: .

1k2 figures in n dimensions
Space	Finite						Euclidean	Hyperbolic
n	3	4	5	6	7	8	9	10
Coxeter group	E3=A2A1	E4=A4	E5=D5	E6	E7	E8	E9 = ${\displaystyle {\tilde {E}}_{8}}$ = E8+	E10 = ${\displaystyle {\bar {T}}_{8}}$ = E8++
Coxeter diagram
Symmetry (order)	[3−1,2,1]	[30,2,1]	[31,2,1]	[[32,2,1]]	[33,2,1]	[34,2,1]	[35,2,1]	[36,2,1]
Order	12	120	1,920	103,680	2,903,040	696,729,600	∞
Graph							-	-
Name	1−1,2	102	112	122	132	142	152	162

Geometric folding

The 1₂₂ is related to the 24-cell by a geometric folding E6 → F4 of Coxeter-Dynkin diagrams, E6 corresponding to 1₂₂ in 6 dimensions, F4 to the 24-cell in 4 dimensions. This can be seen in the Coxeter plane projections. The 24 vertices of the 24-cell are projected in the same two rings as seen in the 1₂₂.

E6/F4 Coxeter planes
122	24-cell
D4/B4 Coxeter planes
122	24-cell

Tessellations

This polytope is the vertex figure for a uniform tessellation of 6-dimensional space, 2₂₂, .

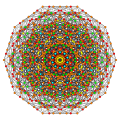
Rectified 122 polytope

Rectified 122
Type	Uniform 6-polytope
Schläfli symbol	2r{3,3,32,1} r{3,32,2}
Coxeter symbol	0221
Coxeter-Dynkin diagram	or
5-faces	126
4-faces	1566
Cells	6480
Faces	6480
Edges	6480
Vertices	720
Vertex figure	3-3 duoprism prism
Petrie polygon	Dodecagon
Coxeter group	E6, [[3,32,2]], order 103680
Properties	convex

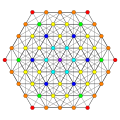
The rectified 1₂₂ polytope (also called 0₂₂₁) can tessellate 6-dimensional space as the Voronoi cell of the E6* honeycomb lattice (dual of E6 lattice).^[5]

Alternate names

• Birectified 2₂₁ polytope
• Rectified pentacontatetrapeton (acronym Ram) - rectified 54-facetted polypeton (Jonathan Bowers)^[6]

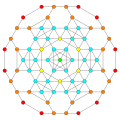
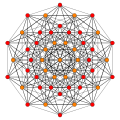
Images

Vertices are colored by their multiplicity in this projection, in progressive order: red, orange, yellow.

Coxeter plane orthographic projections

E6 [12]	D5 [8]	D4 / A2 [6]	B6 [12/2]
A5 [6]	A4 [5]	A3 / D3 [4]

Construction

Its construction is based on the E₆ group and information can be extracted from the ringed Coxeter-Dynkin diagram representing this polytope: .

Removing the ring on the short branch leaves the birectified 5-simplex, .

Removing the ring on the either 2-length branch leaves the birectified 5-orthoplex in its alternated form: t₂(2₁₁), .

The vertex figure is determined by removing the ringed node and ringing the neighboring ring. This makes 3-3 duoprism prism, {3}×{3}×{}, .

Seen in a configuration matrix, the element counts can be derived by mirror removal and ratios of Coxeter group orders.^[3][7]

E6		k-face	fk	f0	f1	f2			f3					f4					f5			k-figure	notes
A2A2A1		( )	f0	720	18	18	18	9	6	18	9	6	9	6	3	6	9	3	2	3	3	{3}×{3}×{ }	E6/A2A2A1 = 72*6!/3!/3!/2 = 720
A1A1A1		{ }	f1	2	6480	2	2	1	1	4	2	1	2	2	1	2	4	1	1	2	2	{ }∨{ }∨( )	E6/A1A1A1 = 72*6!/2/2/2 = 6480
A2A1		{3}	f2	3	3	4320	*	*	1	2	1	0	0	2	1	1	2	0	1	2	1	Sphenoid	E6/A2A1 = 72*6!/3!/2 = 4320
				3	3	*	4320	*	0	2	0	1	1	1	0	2	2	1	1	1	2
A2A1A1				3	3	*	*	2160	0	0	2	0	2	0	1	0	4	1	0	2	2	{ }∨{ }	E6/A2A1A1 = 72*6!/3!/2/2 = 2160
A2A1		{3,3}	f3	4	6	4	0	0	1080	*	*	*	*	2	1	0	0	0	1	2	0	{ }∨( )	E6/A2A1 = 72*6!/3!/2 = 1080
A3		r{3,3}		6	12	4	4	0	*	2160	*	*	*	1	0	1	1	0	1	1	1	{3}	E6/A3 = 72*6!/4! = 2160
A3A1				6	12	4	0	4	*	*	1080	*	*	0	1	0	2	0	0	2	1	{ }∨( )	E6/A3A1 = 72*6!/4!/2 = 1080
		{3,3}		4	6	0	4	0	*	*	*	1080	*	0	0	2	0	1	1	0	2
		r{3,3}		6	12	0	4	4	*	*	*	*	1080	0	0	0	2	1	0	1	2
A4		r{3,3,3}	f4	10	30	20	10	0	5	5	0	0	0	432	*	*	*	*	1	1	0	{ }	E6/A4 = 72*6!/5! = 432
A4A1				10	30	20	0	10	5	0	5	0	0	*	216	*	*	*	0	2	0		E6/A4A1 = 72*6!/5!/2 = 216
A4				10	30	10	20	0	0	5	0	5	0	*	*	432	*	*	1	0	1		E6/A4 = 72*6!/5! = 432
D4		{3,4,3}		24	96	32	32	32	0	8	8	0	8	*	*	*	270	*	0	1	1		E6/D4 = 72*6!/8/4! = 270
A4A1		r{3,3,3}		10	30	0	20	10	0	0	0	5	5	*	*	*	*	216	0	0	2		E6/A4A1 = 72*6!/5!/2 = 216
A5		2r{3,3,3,3}	f5	20	90	60	60	0	15	30	0	15	0	6	0	6	0	0	72	*	*	( )	E6/A5 = 72*6!/6! = 72
D5		2r{4,3,3,3}		80	480	320	160	160	80	80	80	0	40	16	16	0	10	0	*	27	*		E6/D5 = 72*6!/16/5! = 27
				80	480	160	320	160	0	80	40	80	80	0	0	16	10	16	*	*	27

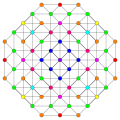
Truncated 122 polytope

Truncated 122
Type	Uniform 6-polytope
Schläfli symbol	t{3,32,2}
Coxeter symbol	t(122)
Coxeter-Dynkin diagram	or
5-faces	72+27+27
4-faces	32+216+432+270+216
Cells	1080+2160+1080+1080+1080
Faces	4320+4320+2160
Edges	6480+720
Vertices	1440
Vertex figure	( )v{3}x{3}
Petrie polygon	Dodecagon
Coxeter group	E6, [[3,32,2]], order 103680
Properties	convex

Alternate names

• Truncated 1₂₂ polytope

Construction

Its construction is based on the E₆ group and information can be extracted from the ringed Coxeter-Dynkin diagram representing this polytope: .

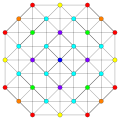
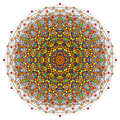
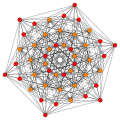
Images

Vertices are colored by their multiplicity in this projection, in progressive order: red, orange, yellow.

Coxeter plane orthographic projections

E6 [12]	D5 [8]	D4 / A2 [6]	B6 [12/2]
A5 [6]	A4 [5]	A3 / D3 [4]

Birectified 122 polytope

Birectified 122 polytope
Type	Uniform 6-polytope
Schläfli symbol	2r{3,32,2}
Coxeter symbol	2r(122)
Coxeter-Dynkin diagram	or
5-faces	126
4-faces	2286
Cells	10800
Faces	19440
Edges	12960
Vertices	2160
Vertex figure
Coxeter group	E6, [[3,32,2]], order 103680
Properties	convex

Alternate names

• Bicantellated 2₂₁
• Birectified pentacontitetrapeton (barm) (Jonathan Bowers)^[8]

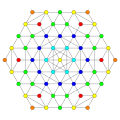
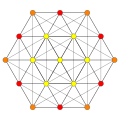
Images

Vertices are colored by their multiplicity in this projection, in progressive order: red, orange, yellow.

Coxeter plane orthographic projections

E6 [12]	D5 [8]	D4 / A2 [6]	B6 [12/2]
A5 [6]	A4 [5]	A3 / D3 [4]

Trirectified 122 polytope

Trirectified 122 polytope
Type	Uniform 6-polytope
Schläfli symbol	3r{3,32,2}
Coxeter symbol	3r(122)
Coxeter-Dynkin diagram	or
5-faces	558
4-faces	4608
Cells	8640
Faces	6480
Edges	2160
Vertices	270
Vertex figure
Coxeter group	E6, [[3,32,2]], order 103680
Properties	convex

Alternate names

• Tricantellated 2₂₁
• Trirectified pentacontitetrapeton (trim or cacam) (Jonathan Bowers)^[9]

See also

• List of E6 polytopes