Riproĉa seslatera kahelaro
From Wikipedia, the free encyclopedia
Remove ads
En geometrio, la riproĉa seslatera kahelaro estas duonregula kahelaro de la eŭklida ebeno. Kiel la nomo sugestas, ĝi povas esti farita per riproĉigo de la regula seslatera kahelaro. Estas kvar trianguloj kaj unu seslatero ĉirkaŭ ĉiu vertico. Ĝia simbolo de Schläfli estas s{3,6} aŭ s{6,3}.
Ĉi tiu kahelaro estas la sola nememspegulsimetria duonregula kahelaro de la eŭklida ebeno.
Remove ads
Vico de rilatantaj pluredroj kaj kahelaroj
La riproĉa seslatera kahelaro estas ero de vico de riproĉigitaj regulaj pluredroj kaj regulaj kahelaroj de la eŭklida kaj hiperbola ebenoj kun verticaj figuroj (3.3.3.3.n).
 Dudekedro (3.3.3.3.3) |
 Riproĉa kubo (3.3.3.3.4) |
 Riproĉa dekduedro (3.3.3.3.5) |
 Riproĉa seslatera kahelaro 3.3.3.3.6 |
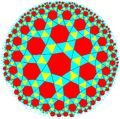 Riproĉa ordo-3 seplatera kahelaro (3.3.3.3.7) |
Riproĉa ordo-3 oklatera kahelaro (3.3.3.3.8) |
Estas nur unu unuformaj kolorigoj de riproĉa seslatera kahelaro. La koloroj estu priskribataj per ciferoj 1, 2, 3. Tiam la 5 edroj (3.3.3.3.6) ĉirkaŭ ĉiu vertico havas kolorojn 11213.
Remove ads
Vidu ankaŭ
- Kahelaro de 2-dimensia ebeno
- Listo de unuformaj ebenaj kahelaroj
Referencoj
- Branko Grünbaum, Shephard G. C.. (1987) Tilings and Patterns - Kahelaroj kaj ŝablonoj. Novjorko: W. H. Freeman. ISBN 0-716-71193-1. (Ĉapitro 2.1: Regulaj kaj unuformaj kahelaroj, p. 58-65)
- Robert Williams, La geometria fundamento de natura strukturo: Fonta libro de dizajno, Novjorko, Dovero, 1979. p39
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads



