Hosoedro

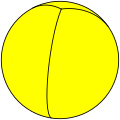
En geometría esférica, un hosoedro n-gonal es un teselado de una superficie esférica mediante lunas, de modo que cada luna comparte los mismos dos vértices polarmente opuestos.

Conjunto de hosoedros n-gonales regulares
Ejemplo de un hosoedro regular hexagonal sobre una esfera
Tipo	Poliedro regular o teselado esférico
Caras	n dígonos
Aristas	n
Vértices	2
Configuración de vértices	2n
Grupo de simetría	Dnh, [2,n], (*22n), orden 4n
Grupo de rotación	Dn, [2,n]+, (22n), orden 2n
Poliedro dual	diedro n-gonal regular
Símbolo de Schläfli	{2,n}
Símbolo de Wythoff	n | 2 2
Símbolo de Coxeter-Dynkin
[editar datos en Wikidata]

Este balón de playa puede considerarse un hosoedro con 6 caras en forma de lunas esféricas, si se quitaran las 2 tapas blancas de los extremos

Un hosoedro n-gonal regular tiene símbolo de Schläfli {2, n}, y cada luna esférica tiene un ángulo interior de 2Π/n radianes (en grados sexagesimales, 360/n).^[1][2]

Hosohedros como poliedros regulares

Véase también: Anexo:Politopos regulares y compuestos

Para un poliedro regular cuyo símbolo de Schläfli es {m, n}, el número de caras poligonales es:

${\displaystyle N_{2}={\frac {4n}{2m+2n-mn}}.}$

Los sólidos platónicos conocidos en la antigüedad son las únicas soluciones enteras para m ≥ 3 y n ≥ 3. La restricción m ≥ 3 impone que las caras poligonales deben tener al menos tres lados.

Al considerar los poliedros como teselados esféricos, esta restricción se puede relajar, ya que los dígonos (2-gonos) se pueden representar como lunas esféricas que tienen áreas distintas de cero.

Permitir que m = 2 hace que

${\displaystyle N_{2}={\frac {4n}{2\times 2+2n-2n}}=n,}$

y admite una nueva clase infinita de poliedros regulares, que son los hosoedros. En una superficie esférica, el poliedro {2, n} se representa como n lunas contiguas, con ángulos interiores de 2Π/n. Todas estas lunas esféricas comparten dos vértices comunes.

Un hosoedro trigonal regular, {2,3}, representado como un mosaico de 3 lunas esféricas sobre una esfera.

Un hosoedro tetragonal regular, {2,4}, representado como un mosaico de 4 lunas esféricas sobre una esfera.

Familia de hosoedros regulares · * n22 mutaciones de simetría de teselados de hosoedros regulares: nn

Espacio	Esférico													Euclídeo
Nombre del teselado	(Monogonal) Monógono	Hosohedro digonal	(Triangular) Hosohedro trigonal	(Tetragonal) Hosohedro cuadrado	Hosohedro pentagonal	Hosoedro hexagonal	Hosoedro heptagonal	Hosoedro octogonal	Hosoedro eneagonal	Hosoedro decagonal	Hosoedro hendecagonal	Hosoedro dodecagonal	...	Hosoedro apeirogonal
Imagen del teselado													...
Símbolo de Schläfli	{2,1}	{2,2}	{2,3}	{2,4}	{2,5}	{2,6}	{2,7}	{2,8}	{2,9}	{2,10}	{2,11}	{2,12}	...	{2,∞}
Diagrama de Coxeter-Dynkin													...
Caras y aristas	1	2	3	4	5	6	7	8	9	10	11	12	...	∞
Vértices	2												...	2
Configuración de vértices	2	2.2	23	24	25	26	27	28	29	210	211	212	...	2∞

Simetría caleidoscópica

Las caras 2n digonales en forma de lunas esféricas de un hosoedro 2n, {2,2n}, representan los dominios fundamentales de la simetría diedral en tres dimensiones: la simetría cíclica C_nv, [n], (* nn), orden 2n. Los dominios de reflexión se pueden mostrar mediante lunas de colores alternativos como imágenes en un espejo.

Bisecar cada luna en dos triángulos esféricos crea una bipirámide n-gonal, que representa el grupo diedral D_nh, orden 4n.

Simetría (orden 2n)	Cnv, [n]	C1v, [ ]	C2v, [2]	C3v, [3]	C4v, [4]	C5v, [5]	C6v, [6]
2n-gonal hosoedro	Símbolo deSchläfli {2,2n}	{2,2}	{2,4}	{2,6}	{2,8}	{2,10}	{2,12}
Imagen	Dominios fundamentales en colores alternativos

Relación con el sólido de Steinmetz

El hosoedro tetragonal es topológicamente equivalente al sólido de Steinmetz bicilíndrico, la intersección de dos cilindros en ángulos rectos.^[3]

Poliedros derivados

El dual del hosoedro n-gonal {2, n} es el diedro n-gonal, {n, 2}. El poliedro {2,2} es auto-dual, y es a la vez hosoedro y diedro.

Un hosoedro se puede modificar de la misma manera que los otros poliedros para producir una variación truncada. El hosoedro n-gonal truncado es un prisma n-gonal.

Hosoedro apeirogonal

En el límite, el hosoedro se convierte en un hosoedro apeirogonal como una teselación bidimensional:

Hosotopos

Véase también: Anexo:Politopos regulares y compuestos

Los análogos de multidimensionales en general se denominan hosotopos. Un hosotopo normal con símbolo de Schläfli {2, p, ..., q} tiene dos vértices, cada uno con una figura de vértice {p, ..., q}.

El hosotopo bidimensional, {2}, es un dígono.

Etimología

El término “hosoedro” parece derivar del griego ὅσος ( hosos ) “tantos”, la idea es que un hosoedro puede tener “ 'tantas' caras como se desee”.^[4] Fue introducido por Vito Caravelli en el siglo XVIII.^[5]

Véase también

• Poliedro
• Politopo