Poliedro esférico

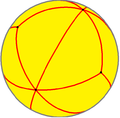
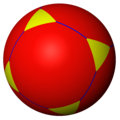
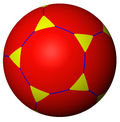
En matemáticas, un poliedro esférico o teselado esférico, es un enlosado de una esfera en el que la superficie está dividida o seccionada por curvas en regiones delimitadas llamadas polígonos esféricos. Gran parte de la teoría de poliedros simétricos se deduce consistentemente de esta manera.

El poliedro esférico más familiar es el balón de fútbol, obtenido a partir de un icosaedro truncado

Este balón de playa sería un hosoedro con 6 caras en forma de lunas esféricas si se quitaran las 2 tapas blancas de los extremos

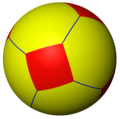
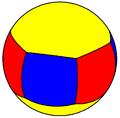
El poliedro esférico más conocido es el balón de fútbol, considerado un icosaedro truncado esférico. El siguiente poliedro esférico más popular es el balón de playa, considerado como un hosoedro.

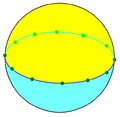
Algunos poliedros "impropios", como los hosoedros y sus duales (diedros), existen como poliedros esféricos, pero sus análogos de caras planas son elementos degenerados. La pelota de playa hexagonal de la imagen, {2, 6}, es un hosoedro, y el diedro {6, 2} es su poliedro dual.

Historia

Los primeros poliedros artificiales conocidos son los poliedros esféricos labrados en piedra. Se han encontrado muchos en Escocia y parecen datar del período neolítico.

Durante el siglo X, el erudito islámico Abu'l-Wafa escribió el primer estudio riguroso sobre poliedros esféricos.

A principios del siglo XIX, el matemático francés Louis Poinsot utilizó poliedros esféricos para descubrir los cuatro poliedros estrellados regulares.

A mediados del siglo XX, Coxeter los utilizó para enumerar todos menos uno de los poliedros uniformes, mediante la construcción de caleidoscópica (construcción de Wythoff).

Ejemplos

Todo poliedro regular, poliedro semirregular y sus duales se pueden proyectar sobre la esfera como teselaciones:

Símbolo de Schläfli	{p,q}	t{p,q}	r{p,q}	t{q,p}	{q,p}	rr{p,q}	tr{p,q}	sr{p,q}
Configuración de vértices	pq	q.2p.2p	p.q.p.q	p.2q.2q	qp	q.4.p.4	4.2q.2p	3.3.q.3.p
Simetría tetraédrica (3 3 2)	33	3.6.6	3.3.3.3	3.6.6	33	3.4.3.4	4.6.6	3.3.3.3.3
		V3.6.6	V3.3.3.3	V3.6.6		V3.4.3.4	V4.6.6	V3.3.3.3.3
Simetría octaédrica (4 3 2)	43	3.8.8	3.4.3.4	4.6.6	34	3.4.4.4	4.6.8	3.3.3.3.4
		V3.8.8	V3.4.3.4	V4.6.6		V3.4.4.4	V4.6.8	V3.3.3.3.4
Simetría icosaédrica (5 3 2)	53	3.10.10	3.5.3.5	5.6.6	35	3.4.5.4	4.6.10	3.3.3.3.5
		V3.10.10	V3.5.3.5	V5.6.6		V3.4.5.4	V4.6.10	V3.3.3.3.5
Dihedral example p=6 (2 2 6)	62	2.12.12	2.6.2.6	6.4.4	26	2.4.6.4	4.4.12	3.3.3.6

Teselado de la esfera mediante triángulos esféricos (icosaedro con algunos de sus triángulos esféricos distorsionados)

n	2	3	4	5	6	7	8	10	...
n-prisma (2 2 p)									...
n-bipirámide (2 2 p)									...
n-antiprisma									...
n-trapezoedro									...

Casos impropios

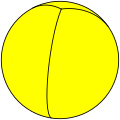
Los teselados esféricos permiten casos que los poliedros no, a saber, como los hosoedros (con códigos de Schläfli del tipo {2, n}) y los diedros (con códigos de Schläfli del tipo {n, 2}). Generalmente, se utilizan hosoedros regulares y diedros regulares.

Familia de hosoedros regulares · * n22 mutaciones de simetría de teselados de hosoedros regulares: nn

Espacio	Esférico													Euclídeo
Nombre del teselado	(Monogonal) Monógono	Hosohedro digonal	(Triangular) Hosohedro trigonal	(Tetragonal) Hosohedro cuadrado	Hosohedro pentagonal	Hosoedro hexagonal	Hosoedro heptagonal	Hosoedro octogonal	Hosoedro eneagonal	Hosoedro decagonal	Hosoedro hendecagonal	Hosoedro dodecagonal	...	Hosoedro apeirogonal
Imagen del teselado													...
Símbolo de Schläfli	{2,1}	{2,2}	{2,3}	{2,4}	{2,5}	{2,6}	{2,7}	{2,8}	{2,9}	{2,10}	{2,11}	{2,12}	...	{2,∞}
Diagrama de Coxeter-Dynkin													...
Caras y aristas	1	2	3	4	5	6	7	8	9	10	11	12	...	∞
Vértices	2												...	2
Configuración de vértices	2	2.2	23	24	25	26	27	28	29	210	211	212	...	2∞

Familia de diedros regulares · *n22 mutaciones de simetría de teselados diedros regulares: nn

Espacio	Esférico							Euclídeo
Nombre del teselado	(Hengonal) Monógono	Diedro	(Triangular) Diedro	(Tetragonal) Diedro cuadrado	Diedro	Diedro	...	Diedro apeirogonal
Imagen del teselado							...
Símbolo de Schläfli	{1,2}	{2,2}	{3,2}	{4,2}	{5,2}	{6,2}	...	{∞,2}
Diagrama de Coxeter-Dynkin							...
Caras	2 {1}	2 {2}	2 {3}	2 {4}	2 {5}	2 {6}	...	2 {∞}
Aristas y vértices	1	2	3	4	5	6	...	∞
Configuración de vértices	1.1	2.2	3.3	4.4	5.5	6.6	...	∞.∞

Relación con las teselaciones del plano proyectivo

Los poliedros esféricos que tienen al menos una simetría inversiva están relacionados con los poliedros proyectivos^[1] (teselados del plano proyectivo real) - así como la esfera tiene un espacio recubridor 2 a 1 del plano proyectivo, los poliedros proyectivos corresponden respecto al doble recubrimiento a los poliedros esféricos que son simétricos bajo simetría central.

Los ejemplos más conocidos de estos poliedros son los poliedros proyectivos regulares, los cocientes de los sólidos platónicos con simetría central, así como dos clases infinitas de diedros y hosoedros:^[2]

• Hemicubo, {4.3} / 2
• Hemioctaedro, {3,4} / 2
• Hemidodecaedro, {5.3} / 2
• Hemicosaedro, {3.5} / 2
• Hemidihedro, {2β, 2} / 2, p> = 1
• Hemihosoedro, {2.2p} / 2, p> = 1

Véase también

• Geometría esférica
• Trigonometría esférica
• Poliedro
• Poliedro proyectivo
• Poliedro toroidal
• Notación de Conway poliedral