Ostertz

Ostertza —ezaguna, baita ere, ortzi-muga, zerumuga, zeruertz edo horizonte izenez— puntu batetik ikus daitekeen Lurraren gainazaleko azken lerroa da, zerua eta lurra (itxuraz) banatzen dituena. Lerro hori, berez, behatzailean zentratzen den Lurraren gainazalaren zirkunferentzia bat da.

Artikulu hau zeruak eta lurrak bat egiten duten lerroari buruzkoa da; beste esanahietarako, ikus «Horizonte (argipena)».

Ostertza, itsasoan.

Bestelako definizio sakonago bat emanez, ostertza Lurraren erdigunetik igarotzen den plano bat litzateke, zenit-nadir lerroarekiko perpendikularra. Honi ostertz astronomikoa esaten zaio. Kasu honetan, zeru-esfera ez dago behatzailean zentratuta, baizik eta Lurraren erdian. Lurraren erradioa zeru-esferaren magnitudearen aurrean baztergarria denez, ostertzaren planoa bat dator behatzailearen begietatik pasatzen den Lurraren erradioarekiko elkarzuta den planoarekin.

Hiru ostertz motaren diagrama

Lurrean, behatzailearen ikuspegiaren arabera, ondoko ostertz mota hauek bereizi ohi dira:  

• Ostertz geometrikoa: behatzailea aurkitzen den puntutik, Lurraren gainazalarekiko ukitzailea den plano ideala da. Behatzaileak ikusiko lukeen zerumuga litzateke, errefrakzioaren alteraziorik ez balego edo naturan objektuen oztoporik ez balego. Ostertz geometrikoak Lurra esferikoa dela onartzen du; ostertz errealak, aldiz, Lurra elipsoide irregularra dela. Errefrakzioa oso txikia denean, behatzaile batek hurbilen ikus dezakeen ostertz erreala itsasoan ikus dezakegun ostertza da.
• Ostertz ikusgaia: lursail, lur-eremu edo beste objektuen oztopoak aurkitu eta argiak aurrera egitea galarazten edo eremu bat mugatuz errefraktatzen den ostertza da. Lurrean gertatzen diren oztopoen artean, giza eraikuntzak eta natur elementuak aurkitu ditzakegu.
• Ostertz astronomikoa (edo ostertz teorikoa): Behatzailaren begi-mailatik igarotzen den plano infinitua da, zenit-nadir lerroarekiko perpendikularra. Kordenatu horizontalen sisteman erabiltzen den erreferentzia-planoa da.

Ostertzen arteko angelua kalkulatzeko erabili ohi izan da aipatu berri den begi mailako plano infinitua, hau da, ostertz astronomikoaren eta ostertz geometrikoaren arteko aldea kalkulatzeko. Bi ostertz hauen arteko aldea bi ostertzen planoen arteko angelua da, hain zuzen ere, eta izarren bidezko nabigazioan kontuan hartzen den faktore garrantzitsu bat da.

Ostertzaren irudia, Biarritzeko kostatik, non Lurraren kurbadura ikus daitekeen.

Ostertzaren neurketak nola ezarri

Ostertza koordenatu sistema astronomiko batzuetarako funtsezko planoa da; beraz, hau ongi ezartzea ezinbestekoa izango da neurketak ahalik eta zehatzenak izateko. Hori da, adibidez, koordenatu horizontalen sistema geozentrikoen kasua, non izar edo planeten ostertzaren gaineko altuerak hartu behar diren. In situ lortutako neurketak, hasiera batean, itxurazko ostertzari zuzendutakoak izango dira, eta errefrakzio atmosferiko eta paralaxiaren bidez zuzendu beharko dira, ostertz astronomikoari dagokion altuera lortzeko.

Paralaxia ostertzaren altuerarekiko gutxitzen da, zenitean nulua bihurtzen den arte. Hau zuzentzeko, zehaztasun handiko neurrietarako, Lurra elipsoidetzat hartu behar da, eta ez esferatzat, nahiz eta egiaz Lurra geoide bat den. Horretarako, ezinbestekoa da behaketa egiten den puntu zehatzetik Lurraren erdigunera dagoen distantzia osoa kontuan hartzea, eta ez batez besteko erradioa. Oso urruneko izarren kasuan, baliteke altuerako paralaxia esanguratsua ez izatea.

Errefrakzioari dagokionez, horizontearen gainetik 0º-ra 34' inguru balio du. Eguzkiaren diametro angeluarra 32' ingurukoa denez, Eguzkiaren diskoak itsasoa ukitzen duenean, haren irudia errefraktatua ikusten dugu; izan ere, Eguzkia gure horizonte optikoaren gainetik eta gure horizonte geometrikoaren azpitik dago une horretan. Errefrakzioa txikiagotu egiten da horizontearen gaineko altuera handituz joan ahala, altuerako paralaxiarekin gertatzen den bezala, eta zenitean deuseztatu egiten da.

Ostertzaren itxura

Historikoki, guretzat ikusgaia den ostertzeraino dagoen distantzia ezagutzea ezinbestekoa izan da nabigaziorako eta gizakiaren biziraupenerako, batez ere itsasoan. Distantzia honek behatzailearen ikusmen maximoa mugatzen du eta, hainbat mendez, komunikatzeko eta informazioa igortzeko gizakien arteko oztopo garrantzitsu bat izan da, nahiz eta garrantzi hori gutxitzen joan den irratiaren eta telegrafoaren garapenarekin.

Marrazketako perspektiba eta ihespuntua.

Hala ere, gaur egun oraindik ikus daiteke ostertzak duen garrantzia garraiorako; izan ere, aireontziak Visual Flight Rules (VFR) arauei jarraituz hegan doazenean, aireontzia menderatuta gidatzeko ondorengo teknika erabiltzen da: hegaldiaren altitudea. Pilotuak, teknika honen bitartez, aireontziaren muturrak eta ostertzak osatzen duten harreman bisuala erabiltzen du ostertza erreferentzia gisa hartuz. Honez gain, pilotuek haien orientazio espaziala mantentzeko ere erabiltzen dute ostertzaren erreferentzia.

Perspektiba bidezko marrazketan eta beste testuinguru batzuetan Lurraren kurbadura ez da kontuan hartzen; beraz, edozein plano horizontalen puntuek bat egiten duten lerro teorikotzat hartzen da ostertz terminoa (irudiaren planoaren gainean proiektatzen denean), non behatzailearekiko distantzia handitzen doan bertara hurbildu heinean. 

Itsas mailatik gertu dauden behatzaileentzat, hautemanezina da ostertz geometrikoaren (erabat laua den lur-plano infinitua hartzen duenaren) eta benetako ostertzaren (Lurraren gainazal esferikoa hartzen duenaren) arteko aldea begi hutsez. Hala ere, 1000 m-ko mendixka batean itsasoari begira dagoen pertsonarentzat, benetako ostertzak gradu bateko desbideraketa negatiboa izango du lerro horizontal batekin alderatuta.

Astronomian, ostertza behatzailearen begien pareko plano horizontala da. Koordenatu horizontalen sistemaren oinarrizko planoa da, zero graduko altitudea duten puntuen leku geometrikoa. Forma aldetik horizonte geometrikoaren antzekoa bada ere, testuinguru honetan ostertza planotzat har daiteke espazioan, irudi-plano bateko lerro baten modura hartu beharrean.

Ostertzerainoko distantzia  

Kalkulua  

Tangente-sekantearen teorema.

Lurra esfera perfektu bat dela jota (esferoide baten ordez), eta atmosferaren errefrakzioaren eragina kontuan hartu gabe, zeruertzarekiko distantzia erraz kalkula daiteke.  ^[1]

Tangente-sekantearen teoremak hau ezartzen du: ^[2] 

${\displaystyle {\text{OC}}^{2}={\text{OA}}\times {\text{OB}}}$

Eta hurrengo aldaketak eginda:  

• ${\displaystyle d}$ = ${\displaystyle {\text{OC}}}$ = ostertzerainoko distantzia;  

• ${\displaystyle D}$ = ${\displaystyle {\text{AB}}}$ = Lurraren diametroa;  

• ${\displaystyle h}$= ${\displaystyle {\text{OB}}}$= behatzailearen altuera itsas mailarekiko;  

• ${\displaystyle D+h}$ = ${\displaystyle {\text{OA}}}$ =Lurraren diametroaren eta itsas mailarekiko behatzailearen altueraren arteko batura,

non ${\displaystyle d}$, ${\displaystyle R}$ eta ${\displaystyle h}$ unitate berberetan neurtuak dauden.  

Formula berria honako hau da:  

${\displaystyle d^{2}=h(D+h)}$

edo

${\displaystyle d=}{\sqrt {h(D+h)}}{=}{\sqrt {h(2R+h)}}{=}{\sqrt {2Rh+h^{2}}}{,}$

Ostertzerainoko distantzia geometrikoaren kalkulua, Pitagorasen teorema erabiliz.

non ${\displaystyle R}$ Lurraren erradioa den (6378,1 km).

Ekuazio bera lor daiteke Pitagorasen teorema erabiliz. Ostertzean, ${\displaystyle {\overline {HO}}}$ ikus-lerroa Lurrarekiko ukitzailea da, eta ${\displaystyle R}$ Lurraren erradioarekiko perpendikularra da. Horrek triangelu angeluzuzena eratzen du, behatzailearen erradioa eta ${\displaystyle h}$ altuera batuz ${\displaystyle (R+h)}$ eta hipotenusatzat hartuz. Orduan:  ^[1][3][4][5]

${\displaystyle d^{2}+R^{2}=(R+h)^{2};}$

eta ${\displaystyle d}$ isolatuz:  

${\displaystyle d=}{\sqrt {(R+h)^{2}-R^{2}}}{;}$

eta ${\displaystyle (R+h)^{2}}$ terminoa garatuz, ${\displaystyle R^{2}}$ terminoak beraien artean deuseztatzen dira:  

${\displaystyle d=}{\sqrt {2Rh+h^{2}}}{.}$

Adibidez, satelite bat 2000 km-ko altitudean badago, ostertzarekiko distantzia 5430 kilometrokoa izango da.

Hurbilketa

Ostertzerainoko distantzien irudikapen logaritmikoa, h altuera jakin baterako, non s Lurraren gainazalean zeharreko distantzia den, d lerro zuzeneko distantzia eta ~d lerro zuzeneko gutxi gorabeherako distantzia, h Lurraren erradioa (6371 km) baino askoz txikiagoa dela suposatuz.

Behatzailea lurrazaletik gertu badago, baliozkoa da ${\displaystyle h^{2}}$ baztertzea ${\displaystyle (2Rh+h^{2})}$^[3][4] terminoan; eta orduan:  

${\displaystyle d\approx }{\sqrt {2Rh}}{}$

𝑑 eta 𝑅 kilometrotan eta ℎ metrotan adierazita, eta Lurraren batez besteko erradioa 6371 km bezala hartuz, zeruertzarekiko distantzia ondorengoa da: ^[5] 

${\displaystyle d\approx }{\sqrt {2\cdot 6371\cdot h/1000}}{\approx 3.57}{\sqrt {h}}{.}$

Gainazaletik 1,5 metrora, orduan, ostertza 4,4 km ingurura dago; hegazkin batetik 10.000 m-ko altitudean, ostertza ia 360 km-ra dago; eta orbitan dagoen Nazioarteko Espazio Estaziotik, 420 km-ko altueran, ostertza 2.300 km baino gehiagora dago. ^[5]  Neurri-unitate anglosaxoiak erabiliz, ${\displaystyle d}$ eta ${\displaystyle R}$ miliatan eta ${\displaystyle h}$ oinetan, ondoko hau da horizontearekiko distantzia:  

${\displaystyle d\approx }{\sqrt {2\cdot 3963\cdot h/5280}}{\approx }{\sqrt {1.5h}}{\approx 1.22{\sqrt {h}}.}$

${\displaystyle d}$ itsas miliatan eta ${\displaystyle h}$ oinetan badago, faktore konstantea gutxi gorabehera 1,06 da, eta hori 1etik nahiko hurbil dago. Ondorioz,  egoera horretan, ondoko hurbilketa dugu:  

${\displaystyle d\approx }{\sqrt {h}}{}$

Formula hauek ${\displaystyle h}$ Lurraren erradioa baino askoz txikiagoa denean erabil daitezke (6371 km edo 3959 milia), edozein mendiren gailurretik, edozein hegazkinetatik edo altuera handiko globotik batetik dauden bista guztiak barne. Emandako konstanteekin, formula metrikoek zein inperialek % 1eko zehaztasuna dute. ${\displaystyle h}$ adierazgarria bada ${\displaystyle R}$-rekiko, satelite gehienekin gertatzen den bezala, hurbilketa jada ez da baliozkoa eta formula zehatza behar da.

Ostertzarekin harremana daukaten neurriak

Arku-luzera

Erlazio honek arku-luzeran zehar ${\displaystyle s}$ zirkulu maximoak Lurraren gainazal kurbatutik horizontera duen distantzia ortodromikoa adierazten du, zuzen konpara daitekeena mapa bateko distantzia geografikoarekin.

Aurreko ataleko horizonterako distantzia geometrikoaren diagramatik, radianetako ${\displaystyle \gamma }$ terminotan formula daiteke:

${\displaystyle s=R\gamma$ ;}

orduan,

${\displaystyle \cos \gamma =\cos {\frac {s}{R}}={\frac {R}{R+h}}}$

eta ${\displaystyle s}$ askatuz,

${\displaystyle s=R\arccos {\frac {R}{R+h}}.}$

${\displaystyle s}$ distantzia ${\displaystyle d}$ ikus-lerroaren distantziaren arabera ere adieraz daiteke

${\displaystyle \tan \gamma ={\frac {d}{R}}.}$

Beraz, ${\displaystyle \gamma }$ ordezkatuz eta berrantolatuz,

${\displaystyle s=R\arctan {\frac {d}{R}}}$

${\displaystyle d}$ eta ${\displaystyle s}$ distantziak ia berdinak dira objektuaren altuera gutxiesgarria denean erradioaren aldean (hau da, ${\displaystyle h}$${\displaystyle \ll }$${\displaystyle R}$).

Angelu zenitala

Angelu zenital maximoa behatzailearentzat, atmosfera esferiko homogeneoan goratua.

Behatzailea goratuta dagoenean, ostertzaren angelu zenitala 90º baino handiagoa izan daiteke. Izpia Lurraren gainazalaren ukitzailea denean gehienezko angelu zenitala sortzen da; eskuineko irudian, OCG triangeluarena,

${\displaystyle \cos \gamma ={\frac {R}{R+h}},}$

non ${\displaystyle h}$ behatzaileak gainazalean daukan altuera baita, eta ${\displaystyle \gamma }$ ostertzaren okerdura angeluarra. Azken honek zeruertzaren angelu zenitalarekin ${\displaystyle z}$ daukan lotura honako hau da:

${\displaystyle z=\gamma +90^{\circ }}$

${\displaystyle h}$ altuera ez-negatibo batentzat, ${\displaystyle z}$ angelua beti da ${\displaystyle \geq }$ 90º.

Errefrakzio atmosferikoaren eragina

Lurra Ilargia bezalako airerik gabeko mundua balitz, argiak horizontalki bidaiatuko luke eta aurreko kalkuluak zehatzak izango lirateke. Hala ere, Lurrak aire-atmosfera bat du, eta atmosferaren dentsitatea eta errefrakzio-indizea nabarmen aldatzen dira tenperaturaren eta presioaren arabera. Horren ondorioz, aireak argia gradu desberdinetan errefraktatzen du; honek ostertzaren itxurari eragiten dio.^[6]

Oro har, Lurraren gainazaletik gertu dagoen airearen dentsitatea handiagoa da altuera handietan aurkitu daitekeenarena baino. Ondorioz, bere errefrakzio-indizea handiagoa da lurrazaletik gertu gorago baino. Horrek ia horizontalki bidaiatzen duen argia beherantz errefraktatzea eragiten du. Horren ondorioz, ostertzarekiko distantzia erreala handiagoa da formula geometrikoekin kalkulatutako distantzia baino.  

Baldintza atmosferiko estandarrekin, diferentzia %8 ingurukoa da. Horrek goian erabilitako formula metrikoko 3,57 faktorea aldatzen du, 3,86ra,^[3][5] gutxi gorabehera. Zuzenketa hori nahiko hurbilketa ona izan daiteke baldintza atmosferiko normalizatuetan.

Baldintzak ezohikoak direnean, hurbilketa horrek huts egiten du. Tenperatura-gradienteek asko eragiten diote errefrakzioari, eta gradiente horiek asko alda daitezke egun batetik bestera, batez ere uretan. Muturreko kasuetan, normalean udaberrian, aire beroak ur hotzaren tenperatura gainditzen duenean, errefrakzioak ahalbidetzen du argiak Lurraren gainazalari jarraitzea ehunka kilometrotan.  

Kontrako baldintzak, adibidez, basamortuetan gertatzen dira, non azalera hain beroa den, dentsitate txikiko airea aire freskoenaren azpitik baitago. Horren ondorioz, argia gorantz errefraktatzen da, eta ispilatze-efektuak eragiten ditu, eta, ondorioz, ostertz kontzeptuak zentzua galtzen du. Ezohiko kondizioetako errefrakzio-efektuetarako kalkulatutako balioak, beraz, hurbilketak dira.^[3] Hala ere, lehenago deskribatutako hurbilketa sinplea baino zehaztasun handiagoz kalkulatzeko saiakerak egin dira.

Ikus daitekeen uhin-luzeraren tartetik kanpo, errefrakzioa desberdina izango da. Radarrarentzat (adibidez, 300-3 mm-ko uhin-luzeretarako, hau da, 1 eta 100 GHz bitarteko maiztasunetarako), Lurraren erradioa 4/3-z biderkatu daiteke, formula metrikoan 4.12ko faktorea emango duen erradio eraginkorra lortzeko, hau da, horizonte geometrikotik % 15 harago edo bisualetik % 7 harago. 4/3 faktorea ez da zehatza, ikusmenaren kasuan errefrakzioa baldintza atmosferikoen araberakoa baita.

Ostertzaren distantziaren kalkulua errefrakzio atmosferikoak eraginda:

Ostertzaren kurbadura

Ostertzaren kurbadura erraz ikusten da 2008ko argazki honetan, transbordadore espazial batetik egindakoa 226 km-ko altitudean.

Lurraren gainazalaren gaineko puntu batetik, ostertzak ganbil samarra dirudi; arku zirkularra da. Hurrengo formulak kurbadura bisual horren altitudearen eta Lurraren erradioaren arteko oinarrizko erlazio geometrikoa adierazten du:

${\displaystyle \kappa ={\sqrt {\left(1+{\frac {h}{R}}\right)^{2}-1}}}$

Kurbadura hori kurbaduraren erradio angeluarraren elkarrekikoa da radianetan. 1,0-ko kurbadura 57,3º-ko erradio angeluar baten zirkulu gisa agertzen da, Lurraren gainazaletik gutxi gorabehera 2640 km-ko altitudeari (1640 milia) dagokiona. 10 km-ko altitudean (6,2 milia; 33 000 oin), ohiko hegazkin baten altitude tipikoa, ostertzaren kurbadura matematikoa gutxi gorabehera 0,056 da, zirkuluaren ertzaren kurbadura bera, 10 m-ko erradioa duena, eta zuzenean zirkuluaren erdigunetik 56 cm-tik ikusten dena.

Hala ere, itxurazko kurbadura txikiagoa da atmosferako argiaren errefrakzioagatik eta hodei-geruza altuek zeruertza iluntzeagatik sortzen dena baino, geruza horiek ikus-gainazalaren gaineko altitudea murrizten baitute.

Ihes-puntua

Ostertzeko bi puntuak (A eta B) eraikinaren ertzak irudikatzen dituzten segmentuek zabaltzen dituzten lerroen elkarguneetan daude. Ostertzaren lerroa bat dator ate eta leihoen goiko aldeko lerroarekin.

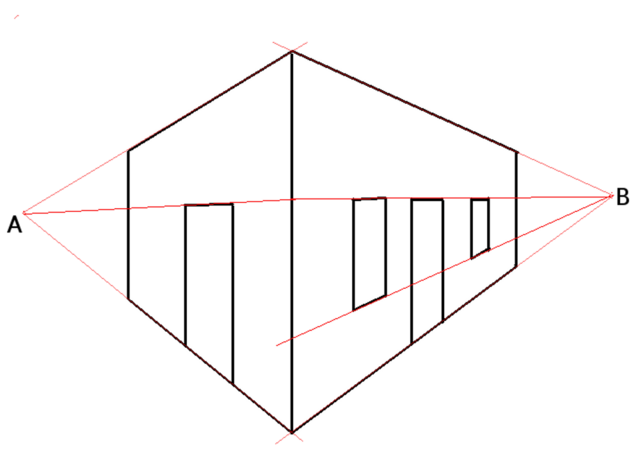
Ostertza irudi-planoaren funtsezko ezaugarria da perspektiba grafikoaren zientzian. Irudi-planoa lurrarekiko bertikala dela joz gero, eta P irudi-planoaren gainean O begi-puntuaren proiekzio perpendikularra dela joz gero, horizontea lerro horizontal gisa definitzen da P-ren bidez. P puntua irudiarekiko perpendikularrak diren lerroen desagertze-puntua da. S ostertzeko beste puntu bat bada, orduan SOrekiko paraleloak diren lerro guztien desagertze-puntua izango da S. Alabaina O-k eta horizonteak zehaztutako horizontearen planoa beste edozein planoren modukoa zela adierazi zuen Brook Taylorrek.