Calcul différentiel

En mathématiques, le calcul différentiel est un sous-domaine de l'analyse qui étudie les variations locales des fonctions. C'est l'un des deux domaines traditionnels de l'analyse, l'autre étant le calcul intégral, utilisé notamment pour calculer l'aire sous une courbe^[1].

Le graphe d'une fonction arbitraire ${\displaystyle y=f(x)}$ (bleu). Graphiquement, la dérivée de ${\displaystyle f}$ en ${\displaystyle x\approx 1.8}$ est le coefficient directeur de la pente (la droite orange, représentant la tangente à la courbe en ${\displaystyle x\approx 1.8}$).

Le calcul de la dérivée d'une fonction est, avec des notions connexes telles que la différentielle et leurs applications (équations différentielles, etc.) l'un des principaux objets d'étude du calcul différentiel. Géométriquement, la dérivée en un point d'une fonction à valeurs réelles est la pente de la tangente au graphe de la fonction en ce point. Pour certaines fonctions et en certains points, la dérivée peut ne pas exister ou ne pas être définie.

Le calcul différentiel a des applications dans de nombreuses disciplines quantitatives.

Histoire

Les premières traces du principe de tangente à une courbe proviennent des mathématiciens grecs antiques, tels qu'Euclide, Archimède, et Apollonios de Perga.

Concernant les calculs d'aires et de volumes, Archimède, célèbre pour son utilisation de la méthode d'exhaustion pour ses démonstrations^[2], utilisait en parallèle une méthode proche de la méthode des indivisibles pour les déterminer^[3],[4]. On peut voir cette méthode comme un ancêtre du calcul intégral.

L'utilisation des infinitésimaux pour étudier un taux de variation en un point est déjà développée par Bhāskara II. Beaucoup de résultats de calcul différentiel ont été retrouvés dans son travail (comme le théorème de Rolle)^[5].

Le calcul différentiel moderne a été créé, suivant deux voies différentes, par Leibniz et Newton^[6]. On devrait y ajouter une troisième voie, contemporaine et indépendante de l'occident, celle de Seki Kōwa, au Japon.^[pas clair]

Dérivée

Le graphe de ${\displaystyle y=x^{2}}$, avec une droite tangente à ${\displaystyle (2,4)}$. La pente de la droite tangente est égale à ${\displaystyle 4}$. (Notez que les axes du graphique ne sont pas à l'échelle 1:1.)

En mathématiques, la dérivée d'une fonction d'une variable réelle mesure l'ampleur du changement de l’image de la fonction (valeur de sortie) par rapport à un petit changement de son argument (valeur d'entrée). Le calcul de dérivées est un outil fondamental du calcul infinitésimal.

Définition formelle

Soit ${\textstyle f:I\to \mathbb {R} }$ une application de ${\textstyle I}$, un intervalle réel d’intérieur ${\displaystyle {\stackrel {\ \circ }{I}}}$ non-vide, dans l'ensemble des nombres réels. On dira que ${\textstyle f}$ est dérivable en un point ${\displaystyle x_{0}\in {\stackrel {\ \circ }{I}}}$ si le taux d'accroissement de ${\displaystyle f}$ en ${\displaystyle x_{0}}$ admet une limite en ${\displaystyle 0}$ : $${\displaystyle \lim _{h\to 0}{\frac {f(x_{0}+h)-f(x_{0})}{x_{0}+h-x_{0}}}=\lim _{h\to 0}{\frac {f(x_{0}+h)-f(x_{0})}{h}}.}$$ Si ${\textstyle f}$ est dérivable en ${\textstyle x_{0}}$, sa dérivée en ${\textstyle x_{0}}$ est égale à la limite du taux d'accroissement. On la note alors ${\displaystyle f'(x_{0})}$ ou ${\displaystyle {\dfrac {\mathrm {d} f}{\mathrm {d} x}}(x_{0})}$. Enfin, si ${\textstyle f}$ est dérivable en tous points de ${\displaystyle I}$, on définit la fonction dérivée de ${\displaystyle f}$ comme l'application :

$${\displaystyle {\begin{aligned}f':I&\longrightarrow \mathbb {\mathbb {R} } \\x&\longmapsto f'(x).\end{aligned}}}$$

La différentielle généralise l'idée de dérivée en un point aux fonction de plusieurs variables ou à valeurs vectorielles, mais n'est pas traitée ici (voir l'article sur la différentielle).

Applications

Exemples de dérivées paraboliques

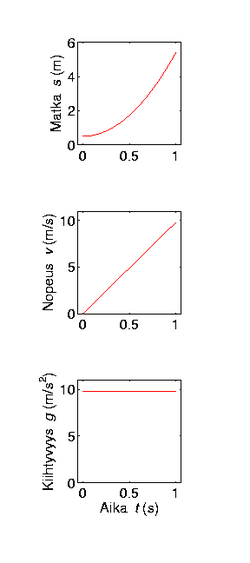
La dérivation a des applications dans presque tous les domaines quantitatifs. Par exemple, les dérivées sont fréquemment utilisées pour trouver les extremums (maximums et minimums, ou maxima et minima en français latin) d'une fonction.

Équations différentielles

Les équations impliquant des dérivées sont appelées équations différentielles. Elles sont fondamentales pour décrire les phénomènes naturels et utilisées dans de nombreuses disciplines scientifiques.

En physique

En mécanique, la vitesse d'un objet est définie par la dérivée de la position de l'objet par rapport au temps. L'accélération est la dérivée de la vitesse par rapport au temps. D'après la deuxième loi de Newton, appelée principe fondamental de la dynamique, la masse ${\displaystyle m}$, supposée constante, d'un objet multipliée par la dérivée du vecteur vitesse de cet objet par rapport au temps est égale à la somme vectorielle des forces ${\displaystyle F_{i}}$ appliquées à cet objet, ce qui s'écrit mathématiquement par l'équation différentielle :

$${\displaystyle {\begin{aligned}m{d{\vec {v}} \over dt}=\sum _{i}{{\vec {\mathrm {F} }}_{i}}.\end{aligned}}}$$

En dynamique des populations

En dynamique des populations, on modélise l'évolution de la taille d'une population. Le nombre d'individus ${\displaystyle N(t)}$ est modélisé par une fonction qui dépend du temps. La vitesse d'évolution est la dérivée de cette fonction : ${\displaystyle N'(t)}$.

Un modèle simple est celui donné par Thomas Malthus. On considère que la vitesse d'évolution de la population est proportionnelle à la population elle-même :

$${\displaystyle {\begin{aligned}N'(t)=\lambda N(t)\end{aligned}}}$$

où ${\displaystyle \lambda }$ est une valeur réelle liée à la natalité et la mortalité de la population. La fonction ${\displaystyle N(t)}$ est connue et donnée par ${\displaystyle N(t)=N_{0}\exp(\lambda t)}$ où ${\displaystyle N_{0}}$ est la population initiale. On parle de croissance exponentielle.

Les équations de Malthus, de Verhulst et de Lotka-Volterra sont des exemples classiques de modèles utilisés en dynamique des populations. Ces relations impliquent généralement un taux de natalité et un taux de mortalité, et parfois les autres espèces du système (par exemple : Équations de prédation de Lotka-Volterra).

Autres

En chimie, la vitesse d'une réaction est donnée par la dérivée de la concentration des espèces chimiques impliquées par rapport au temps.

En recherche opérationnelle, les dérivées permettent de déterminer les moyens les plus efficaces de transporter des matériaux et de concevoir des usines.

Dans un circuit électrique, les grandeurs telles que l'intensité et la tension varient en fonction du temps et sont liées entre elles dans des équations différentielles.

Les dérivées et leurs généralisations apparaissent dans de nombreux domaines des mathématiques, tels que l'analyse complexe, l'analyse fonctionnelle, la géométrie différentielle, la théorie de la mesure et l'algèbre abstraite.

Optimisation

Si f est une fonction différentiable sur ℝ (ou un intervalle ouvert) et x est un extremum local de f, alors la dérivée de f s'annuler en x. Les points où f'(x) = 0 sont appelés points critiques ou points stationnaires (et la valeur de f en x est une valeur critique). Si f n'est pas supposée dérivable partout, alors les points où f n'est pas dérivable sont aussi appelés points critiques.

Si f est dérivable deux fois, alors inversement, un point critique x de f peut être analysé en étudiant la dérivée seconde de f en x :

• si cette valeur est positive, x est un minimum local ;
• si cette valeur est négative, x est un maximum local ;
• si elle s'annule, alors x peut être un minimum local, un maximum local ou aucun des deux. (Par exemple, f(x) = x³ a un point critique en x = 0, qui est un point d'inflexion, donc ni un minimum ni un maximum, alors que f(x) = x⁴ a un minimum en x = 0, et f(x) = – x⁴ a maximum en x = 0).

C'est ce qu'on appelle le test de la dérivée seconde. Une alternative, le test de la dérivée première, implique d'étudier le signe de la fonction dérivée f' des deux côtés du point critique.

La dérivation et la résolution des points critiques constituent donc souvent un moyen simple de trouver des minima ou des maxima locaux, ce qui peut s'avérer utile en optimisation. En vertu du théorème des valeurs extrêmes, une fonction continue sur un intervalle fermé doit atteindre ses valeurs minimales et maximales au moins une fois. Si la fonction est dérivable, les minima et maxima ne peuvent se produire qu'aux points critiques ou aux extrémités.

Ceci a également des applications pour la représentation graphique des fonctions : une fois que les minima et maxima locaux d'une fonction dérivable ont été trouvés, un tracé approximatif du graphique peut être obtenu à partir de l'observation sur la croissance ou la décroissance de la fonction entre les points critiques.

Dans les dimensions supérieures, un point critique d'une fonction à valeurs scalaires est un point où le gradient de la fonction s'annule. Le test de la dérivée seconde peut encore être utilisé pour analyser les points critiques en considérant les valeurs propres de la matrice hessienne des dérivées partielles secondes de la fonction au point critique. Si toutes les valeurs propres sont positives, le point est un minimum local ; si elles sont toutes négatives, il s'agit d'un maximum local. S'il existe quelques valeurs propres positives et quelques valeurs propres négatives, le point critique est appelé « point selle », et si aucun de ces cas ne se présente (c'est-à-dire si certaines des valeurs propres sont nulles), le test est considéré comme non concluant.

Calcul des variations

Un exemple de problème d'optimisation consiste à trouver la courbe la plus courte entre deux points d'une surface, en supposant que la courbe doit également se trouver sur la surface. Si la surface est un plan, la courbe la plus courte est une ligne droite. Mais si la surface est, par exemple, en forme d'œuf, le plus court chemin n'est pas immédiatement clair. Ces chemins sont appelés géodésiques, et l'un des problèmes les plus fondamentaux du calcul des variations consiste à trouver des géodésiques. Un autre exemple consiste à trouver la plus petite surface remplissant une courbe fermée dans l'espace. Cette surface est appelée surface minimale et peut également être trouvée à l'aide du calcul des variations.

Voir aussi

Sur les autres projets Wikimedia :

• calcul différentiel, sur le Wiktionnaire
• Calcul différentiel, sur Wikiversity

• Différentielle
• Dérivée partielle
• Primitive