Arc cosinus

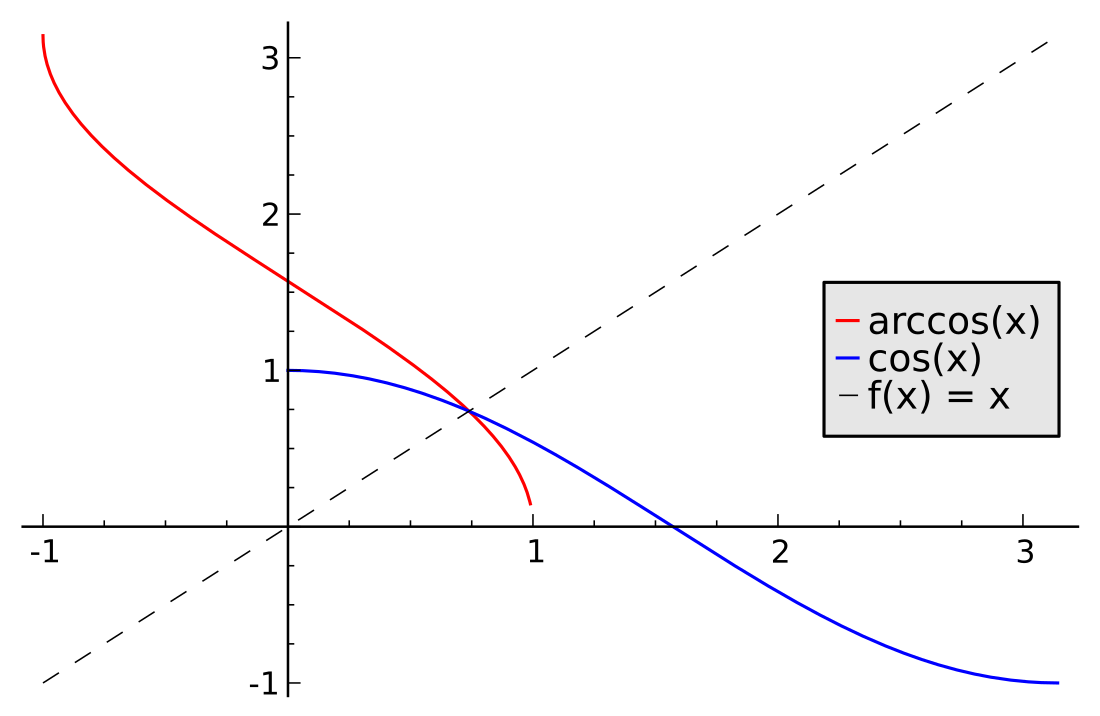
En mathématiques, l’arc cosinus d'un nombre réel compris au sens large entre −1 et 1 est l'unique mesure d'angle dont le cosinus vaut ce nombre, entre l'angle nul (0° ou 0 rad) et l'angle plat (180° ou ${\displaystyle \pi }$ rad).

Fonction arc cosinus

Représentation graphique (dans un repère non normé).

Notation	${\displaystyle \arccos(x)}$
Réciproque	${\displaystyle \cos(x)}$ sur [0 ; π]
Dérivée	${\displaystyle {\frac {-1}{\sqrt {1-x^{2}}}}}$
Primitives	${\displaystyle x\,\arccos(x)-{\sqrt {1-x^{2}}}+C}$

Principales caractéristiques

Ensemble de définition	[−1 ; 1]
Ensemble image	[0 ; π]

modifier - modifier le code - modifier Wikidata

La fonction qui associe à tout nombre réel compris au sens large entre −1 et 1 la valeur de son arc cosinus en radians est notée ${\displaystyle \arccos }$ (${\displaystyle \operatorname {Arccos} }$^[1] ou ${\displaystyle \operatorname {Acos} }$ en notation française, et ${\displaystyle \cos ^{-1}}$, parfois ${\displaystyle \operatorname {acos} }$ ou ${\displaystyle \operatorname {acs} }$ , en notation anglo-saxonne).

Il s'agit alors de la réciproque de la fonction trigonométrique cosinus sur l'intervalle ${\displaystyle [0;\pi ]}$ donc, dans un repère cartésien orthonormé du plan, la courbe représentative de l'arc cosinus s'obtient à partir de la courbe de la restriction du cosinus par la symétrie d'axe la droite d'équation ${\displaystyle y=x}$.

Définition

La fonction ${\displaystyle \arccos$ :[-1,1]\rightarrow [0,\pi ]} est définie comme la fonction réciproque de ${\displaystyle \cos }$ sur ${\displaystyle [0,\pi ]}$, c'est-à-dire qu'il s'agit de l'unique fonction telle que :

$${\displaystyle \forall x\in [0,\pi ]\quad \arccos(\cos x)=x.}$$

En langue naturelle : Pour tout ${\displaystyle x}$ inclus dans l'intervalle de ${\displaystyle 0}$ à π, l'image de la fonction arc cosinus sur l'antécédent cosinus de ${\displaystyle x}$, est ${\displaystyle x}$.

Ensemble de définition

-1 et 1 sont les valeurs minimales et maximales du rapport entre la coordonnée en abscisse du point placé sur le cercle unité, et le rayon du cercle.

Propriétés

Relations trigonométriques

Non-parité

Contrairement aux fonctions arc sinus et arc tangente, la fonction ${\displaystyle \arccos }$ n'admet aucune parité. En revanche, elle possède la propriété suivante^[2] : $${\displaystyle \forall x\in [-1,1]\quad \arccos(-x)=\pi -\arccos x.}$$

Relation avec le sinus

Pour ${\displaystyle X=\arccos x}$, on a ${\displaystyle \sin X\geq 0}$ (car ${\displaystyle X\in [0,\pi ]}$) et ${\displaystyle \cos ^{2}X+\sin ^{2}X=1}$, donc^{[réf. souhaitée]} : $${\displaystyle \sin(\arccos x)={\sqrt {1-x^{2}}}.}$$

« Inversion » des formules trigonométriques

Partant de n'importe quelle formule trigonométrique, on peut l'« inverser », obtenant une relation entre valeurs des fonctions réciproques, mais qui ne sera le plus souvent valable que dans des intervalles restreints. Par exemple, puisque ${\displaystyle \cos 2x=2\cos ^{2}x-1}$, on a ${\displaystyle \arccos \left(2X^{2}-1\right)=2\arccos X}$, mais seulement pour ${\displaystyle X\in [0,1]}$^{[réf. souhaitée]}.

Dérivée

Comme dérivée d'une fonction réciproque, ${\displaystyle \arccos }$ est dérivable sur ${\displaystyle ]-1;1[}$ et vérifie^[3] : $${\displaystyle \arccos 'x={\frac {-1}{\sqrt {1-x^{2}}}}.}$$

Cette formule s'obtient grâce au théorème sur la dérivée d'une fonction réciproque et à la relation avec le sinus (voir supra).

Forme intégrale indéfinie

Cette fonction peut s'écrire sous la forme d'une intégrale indéfinie^[4] : $${\displaystyle \arccos x=\int _{1}^{x}-{\frac {1}{\sqrt {1-t^{2}}}}\,\mathrm {d} t.}$$

Primitives

Les primitives de la fonction ${\displaystyle \arccos }$ s'obtiennent par intégration par parties^[5] : $${\displaystyle \int \arccos(x)~\mathrm {d} x=x\arccos(x)-{\sqrt {1-x^{2}}}+C.}$$

Relation entre arc cosinus et arc sinus

Représentations graphiques d'${\displaystyle \arccos x}$ (en bleu) et d'${\displaystyle \arcsin x}$ (en rouge).

$${\displaystyle \arccos x+\arcsin x={\frac {\pi }{2}}}$$

En effet, ${\displaystyle {\frac {\pi }{2}}-\arccos x}$ est compris entre ${\displaystyle -{\frac {\pi }{2}}}$ et ${\displaystyle {\frac {\pi }{2}}}$ et son sinus est égal au cosinus de ${\displaystyle \arccos x}$, c'est-à-dire à ${\displaystyle x}$, donc ${\displaystyle {\frac {\pi }{2}}-\arccos x=\arcsin x}$.

(Pour une autre méthode, voir « Monotonie et signe de la dérivée » de l'article sur les fonctions monotones.)

Forme logarithmique complexe

On peut exprimer la fonction ${\displaystyle \arccos }$ à l’aide du logarithme complexe^[6] : $${\displaystyle \arccos(x)=-\mathrm {i} \,\ln \left(x+\mathrm {i} \,{\sqrt {1-x^{2}}}\right)={\frac {\pi }{2}}\,+\mathrm {i} \ln \left(\mathrm {i} \,x+{\sqrt {1-x^{2}}}\right)={\frac {\pi }{2}}-\arcsin(x).}$$