נקודת אוכף

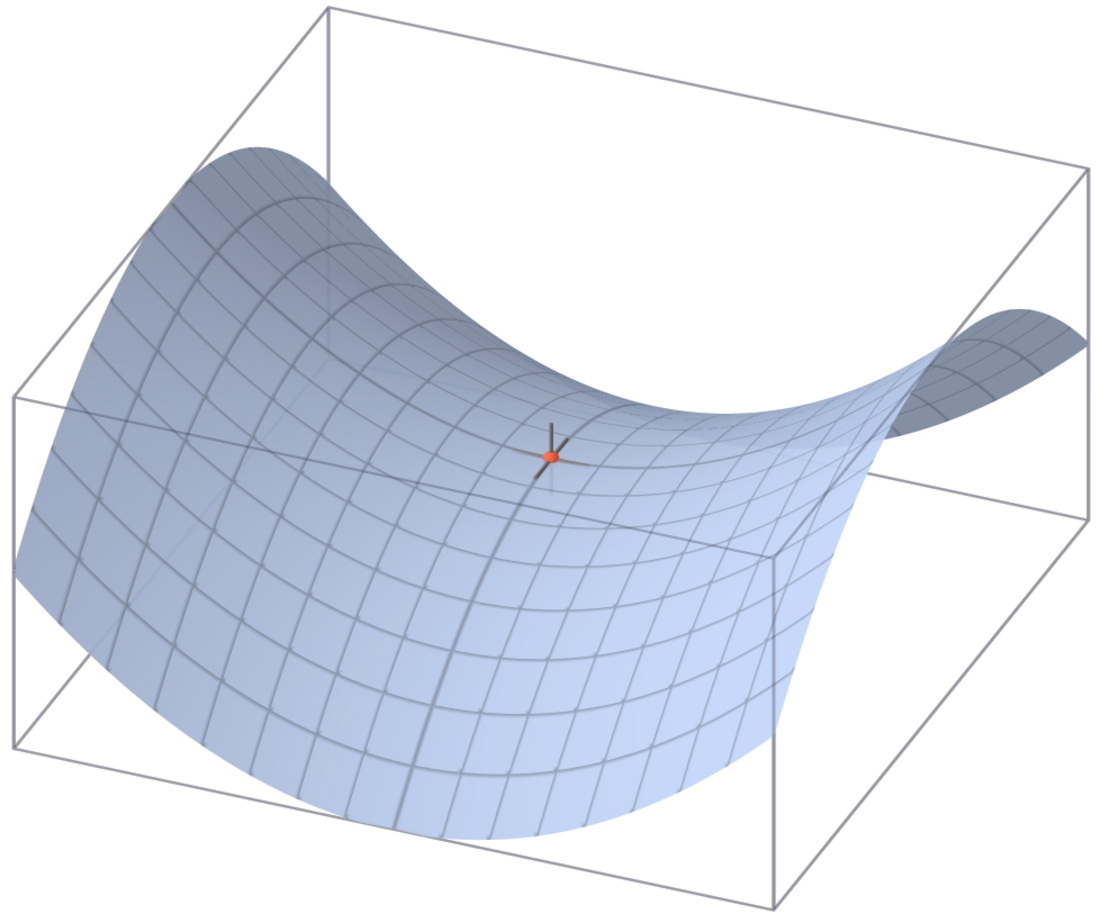
במתמטיקה, נקודת אוכף היא נקודה בתחום של פונקציה של שני משתנים שהיא נקודה יציבה (כלומר, הגרדיאנט שלה מתאפס), אך אינה מהווה נקודת קיצון מקומית. בנקודה כזו, המשטח ידמה לרוב לאוכף אשר מתעקם למעלה בכיוון אחד, אך מתעקם למטה בכיוון אחר (כמו מעבר הרים). בטופוגרפיה, אם נסתכל על מפה טופוגרפית כפונקציה של שני משתנים (אורך ורוחב) המתאימה לכל קואורדינטה גובה, נזהה את נקודת האוכף בדרך כלל באמצעות קו גובה אשר חותך את עצמו (ראו תמונה משמאל).

נקודת אוכף על גרף הפונקציה ${\displaystyle \,z=x^{2}-y^{2}}$ (באדום)

נקודת אוכף בין שתי גבעות, בהצטלבות קו הגובה שבצורת הספרה 8

עם זאת, המשטח בנקודת אוכף לא חייב להיות בצורת אוכף. לדוגמה, לפונקציה ${\displaystyle f(x,y)=x^{2}+y^{3}}$ יש נקודה יציבה ב־${\displaystyle (0,0)}$ שהיא נקודת אוכף משום שהיא איננה נקודת קיצון מקומית, אך גרף הפונקציה באזור הנקודה לא נראה כמו אוכף משום שאין לפונקציה מינימום מקומי בכיוון ציר ה־y ‏(${\displaystyle x=0}$).

הגדרה

תהי ${\displaystyle f(x,y)}$ פונקציה גזירה. נקודת אוכף ${\displaystyle (x_{0},y_{0})}$ של הפונקציה ${\displaystyle f(x,y)}$ היא נקודה יציבה אשר בכל סביבה שלה, ישנן נקודות בתחום ההגדרה של ${\displaystyle f}$ עבורן מתקיים ${\displaystyle f(x,y)<f(x_{0},y_{0})}$ ונקודות בתחום ההגדרה של ${\displaystyle f}$ עבורן מתקיים ${\displaystyle f(x,y)>f(x_{0},y_{0})}$.

עבור פונקציות של יותר מ-2 משתנים, נקודת אוכף של פונקציה חלקה (אשר הגרף שלה הוא עקומה, משטח או משטח רב-ממדי) היא נקודה יציבה אשר בכל סביבה שלה, גרף הפונקציה לא נמצא כולו בצד אחד של המרחב המשיק בנקודה זו.

בממד אחד, נקודת אוכף היא נקודה המהווה הן נקודה יציבה והן נקודת פיתול, ולכן היא אינה נקודת קיצון.

מציאת נקודת אוכף לפי מטריצת הסיאן

שיטה פשוטה לבדיקה האם נקודה יציבה נתונה של פונקציה ממשית ${\displaystyle \,f(x,y)}$ היא נקודת אוכף היא לחשב את מטריצת הסיאן שלה בנקודה זו: אם המטריצה אינה מוחלטת (כלומר, יש לה ערכים עצמיים חיוביים ושליליים), אזי הנקודה תהיה נקודת אוכף.

לדוגמה, מטריצת הסיאן של הפונקציה ${\displaystyle \,z=x^{2}-y^{2}}$ בנקודה היציבה ${\displaystyle \ (0,0)}$ היא:

${\displaystyle {\begin{bmatrix}2&0\\0&-2\\\end{bmatrix}}}$

והיא אכן אינה מוחלטת. מכאן שנקודה זו היא נקודת אוכף. קריטריון זה הוא תנאי מספיק אך לא הכרחי; לדוגמה, הנקודה ${\displaystyle (0,0)}$ היא נקודת אוכף של הפונקציה ${\displaystyle \,z=x^{4}-y^{4},}$, אך מטריצת הסיאן של פונקציה זו בנקודה היא מטריצת האפס, אשר אינה מטריצה לא מוחלטת.

שימושים נוספים

בתורת המשחקים, במשחק סכום אפס בעל שני שחקנים המוגדר במרחב רציף, נקודת שיווי-המשקל היא נקודת אוכף.

באלגברה ליניארית, נקודת אוכף היא האיבר במטריצה שהוא האיבר הקטן ביותר בשורה שלו וגם האיבר הגדול ביותר בעמודה שלו.

לקריאה נוספת

• חשבון אינפיניטסימלי III (יחידה 3), האוניברסיטה הפתוחה, 1984

• Gray, Lawrence F.; Flanigan, Francis J.; Kazdan, Jerry L.; Frank, David H; Fristedt, Bert (1990), Calculus two: linear and nonlinear functions, Berlin: Springer-Verlag, p. 375, ISBN 0-387-97388-5
• Hilbert, David; Cohn-Vossen, Stephan (1952), Geometry and the Imagination (2nd ed.), New York: Chelsea, ISBN 978-0-8284-1087-8
• von Petersdorff, Tobias (2006), "Critical Points of Autonomous Systems", Differential Equations for Scientists and Engineers (MATH 246) lecture notes)
• Widder, D. V. (1989), Advanced calculus, New York: Dover Publications, p. 128, ISBN 0-486-66103-2

קישורים חיצוניים

מדיה וקבצים בנושא נקודת אוכף בוויקישיתוף

• נקודת אוכף, באתר MathWorld (באנגלית)