Timeline
Chat
Prospettiva
Funzione gradino di Heaviside
Da Wikipedia, l'enciclopedia libera
Remove ads
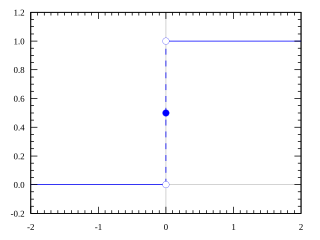
In matematica e fisica, la funzione gradino di Heaviside o funzione a gradino unitaria, il cui nome si deve a Oliver Heaviside, è una funzione discontinua che ha valore zero per argomenti negativi e uno per argomenti positivi. Può essere definita sia come una funzione continua a tratti o come una distribuzione.
La derivata distribuzionale della funzione di Heaviside è la delta di Dirac :
mentre la funzione rampa ne è la primitiva:
La funzione a gradino è usata nella matematica della teoria del controllo e nell'elaborazione dei segnali per rappresentare un segnale che si attiva a partire da un tempo specificato e rimane attivo indefinitamente.
Inoltre tale funzione è utilizzata in fluidodinamica per lo studio di flussi multifase con interfaccia sharp.
Remove ads
Definizione
Riepilogo
Prospettiva
Si indica con:
Spesso, al posto di , si usano le notazioni , o , o ancora, con abuso di notazione, .
Se viene definita come una distribuzione, è la funzione tale per cui:
dove è la derivata di una funzione sufficientemente liscia che decresce all'infinito con andamento sufficientemente rapido.
Una rappresentazione integrale della funzione gradino è la seguente:
Si tratta della funzione di ripartizione di una variabile casuale che è quasi sicuramente 0 (vedi variabile casuale degenere).
La funzione di Heaviside è l'integrale della delta di Dirac:
Il valore di non è del tutto standard: alcuni scrittori assumono , altri La scelta più utilizzata rimane comunque perché permette di ridefinire la funzione di Heaviside attraverso la funzione segno. Questo ne dà una definizione più generale:
Per rimuovere l'ambiguità sul valore di da utilizzare, si può scrivere un pedice che lo specifica:
Tuttavia la stessa notazione è usata per indicare un gradino ritardato:
Il prodotto di una funzione per la funzione dà una funzione unilatera.
Remove ads
Forma discreta
Si può anche definire una forma alternativa del gradino unitario come funzione di una variabile discreta :
dove è intera. Questa funzione è la somma fino a della delta di Kronecker:
dove è la delta di Dirac.
Remove ads
Trasformata di Fourier
Riepilogo
Prospettiva
Un altro modo per scrivere il gradino di Heaviside è
la cui trasformata di Fourier è:
dove è la delta di Dirac. Cioè lo spettro in frequenza del gradino di Heaviside è eccetto che in , dove è presente una singolarità in cui è concentrato lo spettro.
Bibliografia
- Milton Abramowitz e Irene Stegun, Handbook of mathematical functions: with formulas, graphs, and mathematical tables, collana Dover books on mathematics, 9. Dover print.; [Nachdr. der Ausg. von 1972], Dover Publ, 2013, ISBN 978-0-486-61272-0.
- (EN) Bracewell, R. "Heaviside's Unit Step Function, H(x)." The Fourier Transform and Its Applications, 3rd ed. New York: McGraw-Hill, pp. 61-65, 2000.
- (EN) Ram P. Kanwal, Distributional Derivatives of Functions with Jump Discontinuities, Birkhäuser, 1998, pp. 99-137, DOI:10.1007/978-1-4684-0035-9_5, ISBN 978-1-4684-0035-9. URL consultato il 30 giugno 2023.
- (EN) Spanier, J. and Oldham, K. B. "The Unit-Step u(x-a) and Related Functions." Ch. 8 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 63-69, 1987.
Remove ads
Voci correlate
Altri progetti
 Wikimedia Commons contiene immagini o altri file su funzione gradino di Heaviside
Wikimedia Commons contiene immagini o altri file su funzione gradino di Heaviside
Collegamenti esterni
- (EN) Eric W. Weisstein, Heaviside Step Function, su MathWorld, Wolfram Research.
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads

























![{\displaystyle \Theta [n]={\begin{cases}0,&n<0\\1,&n\geq 0,\end{cases}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/18079ee7864c366da97a036f80accb25390d0481)
![{\displaystyle \Theta [n]=\sum _{k=-\infty }^{n}\delta [k],}](http://wikimedia.org/api/rest_v1/media/math/render/svg/dc3a01bdc5326a7eebcb21f8acd74062730169a7)
![{\displaystyle \delta [k]=\delta _{k,0}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/13b9da9ff554d629b0b2b7b05c221007871a1abe)




