クリフォードの定理

幾何学において、クリフォードの定理（クリフォードのていり、英語: Clifford's theorems,Clifford's circle theorems）はイギリスの幾何学者、ウィリアム・キングドン・クリフォードに因み、名づけられた円の交点に関する定理である^[1][2]。

共通の点Mを持つ4円（緑）と、M以外の交点からなる円（茶）。4つの茶色の円は一点で交わる。

5円に対するクリフォードの定理

主張

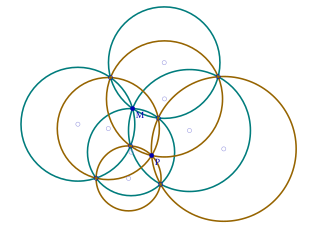
ある点を通り一般の位置（英語版）にある4つの円を描く。つまり、4円が通る点以外に2つの円の交点が延べ6点あり、かつどの3点も共線でないとする。4円から3円選ぶ全ての選び方に対して、3円の、すべてが通る点でない方の交点3つを通る円を新たに作る。このときできた4つの円はある共通点を持つ。この点をP₄とする。

ある点を通り一般の位置にある5つの円を描く。5つの円から4つを選び、その選び方すべてに対して、4円のP₄を定義する。このときできた5つのP₄は共円である。この円をC₅とする。

ある点を通り一般の位置にある6つの円を描く。6つの円から5つを選び、その選び方すべてに対して、5円のC₅を定義する。6つのC₅は共通する点P₆を持つ。

このように、ある一点で交わるn個の円について、nが偶数ならばn個の円C_n-1が、一点で交わり、nが奇数ならばn個の点P_n-1は共円である。これをクリフォードの定理という。

全ての円が通る点で円を反転させて、n本の直線と、それらを辺とする三角形の外接円について共円、共点を示すことによって示すことができる^[3][4]。岡潔の春宵十話では、この形で「クリフォードの定理」として紹介されている^[5][6]。

5円に対するクリフォードの定理の図の反転した形

関連

• オイラー・ポンスレ点
• コックス鎖（英語版）
• 五円定理
• 六円定理
• ミケルの六円定理
• ダオの六角形の周上の六円定理（オランダ語版）
• 七円定理
• 八円定理