일반화 페테르센 그래프

그래프 이론에서 일반화 페테르센 그래프(一般化Petersen graph, 영어: generalized Petersen graph)는 같은 수의 꼭짓점을 갖는 정다각형과 별 모양에서 대응하는 꼭짓점들을 이어 얻는 그래프이다. 특히, 오각형과 오각 별을 이어 얻는 그래프를 페테르센 그래프(영어: Petersen graph)라고 한다.^[1]

정의

3 이상의 정수 ${\displaystyle n\geq 3}$과, ${\displaystyle n}$의 배수가 아닌 정수 ${\displaystyle k\in \mathbb {Z} }$, ${\displaystyle n\nmid k}$가 주어졌다고 하자. 또한, 만약 ${\displaystyle n}$이 짝수라면 ${\displaystyle n/2\nmid k}$라고 하자.

일반화 페테르센 그래프 ${\displaystyle \operatorname {GPG} (n,k)}$는 다음과 같은 그래프이다.

${\displaystyle \operatorname {V} (\operatorname {GPG} (n,k))=\{u_{i},v_{i}\colon i\in \mathbb {Z} /n\}}$

${\displaystyle \operatorname {E} (\operatorname {GPG} (n,k))=\{u_{i}u_{i+1},u_{i}v_{i},v_{i}v_{i+k}\colon i\in \mathbb {Z} /n\}}$

여기서 첨자는 법 ${\displaystyle n}$으로 계산한다. 즉, ${\displaystyle u_{n+i}=u_{i}}$ 및 ${\displaystyle v_{n+i}=u_{i}}$로 간주한다. 일반화 페테르센 그래프의 변 가운데, ${\displaystyle u_{i}v_{i}}$ 꼴의 변을 바큇살(영어: spoke)이라고 한다.

당연히

${\displaystyle \operatorname {GPG} (n,k)=\operatorname {GPG} (n,k+n)=\operatorname {GPG} (n,-k)}$

이므로, 보통

${\displaystyle 1\leq k<n/2}$

를 가정한다.

성질

기초적 성질

페테르센 그래프 ${\displaystyle \operatorname {GPG} (5,2)}$ 속의 완벽 부합

일반화 페테르센 그래프 ${\displaystyle \operatorname {GPG} (n,k)}$는 ${\displaystyle 2n}$개의 꼭짓점과 ${\displaystyle 3n}$개의 변을 가지는 삼차 그래프이며, 완벽 부합을 갖는다. 구체적으로, 위와 같은 표기에서, ${\displaystyle \{u_{i}v_{i}\}_{i\in \mathbb {Z} /n}}$은 완벽 부합을 이룬다.

동형

임의의 정수 ${\displaystyle n\geq 3}$ 및 정수 ${\displaystyle 1\leq k,k'<n/2}$에 대하여, 다음 두 조건이 서로 동치이다.^{[2]:Proposition 9[3]}

• ${\displaystyle \operatorname {GPG} (n,k)\cong \operatorname {GPG} (n,k')}$
• ${\displaystyle kk'\equiv \pm 1{\pmod {n}}}$

예를 들어, ${\displaystyle \operatorname {GPG} (7,2)\cong \operatorname {GPG} (7,3)}$이다.

안둘레

일반화 페테르센 그래프 ${\displaystyle \operatorname {GPG} (n,k)}$의 안둘레는 항상 ${\displaystyle \min\{8,k+3,n/\gcd\{n,k\}\}}$ 이하이다.^{[4]:Theorem 2.1}

증명:

일반화 페테르센 그래프의 꼭짓점 및 변은

${\displaystyle \operatorname {V} (\operatorname {GPG} (n,k))=\{u_{i},v_{i}\colon i\in \mathbb {Z} /n\}}$

${\displaystyle \operatorname {E} (\operatorname {GPG} (n,k))=\{u_{i}u_{i+1},u_{i}v_{i},v_{i}v_{i+k}\colon i\in \mathbb {Z} /n\}}$

이다. 그 속에서

${\displaystyle u_{0}-v_{0}-v_{k}-u_{k}-u_{k+1}-v_{k+1}-v_{1}-u_{1}-u_{0}}$

는 길이 8의 순환이며,

${\displaystyle u_{0}-v_{0}-v_{k}-u_{k}-u_{k-1}-\dotsb -u_{1}-u_{0}}$

는 길이 ${\displaystyle k+3}$의 순환이며,

${\displaystyle v_{0}-v_{k}-v_{2k}-\dotsb -v_{0}}$

는 길이 ${\displaystyle n/\gcd\{n,k\}}$의 순환이다.

또한, 다음이 성립한다.

${\displaystyle \operatorname {girth} (\operatorname {GPG} (ak\pm b,k))\leq a+b+2}$

증명:

일반화 페테르센 그래프의 꼭짓점 및 변은

${\displaystyle \operatorname {V} (\operatorname {GPG} (n,k))=\{u_{i},v_{i}\colon i\in \mathbb {Z} /n\}}$

${\displaystyle \operatorname {E} (\operatorname {GPG} (n,k))=\{u_{i}u_{i+1},u_{i}v_{i},v_{i}v_{i+k}\colon i\in \mathbb {Z} /n\}}$

이다. 그 속에서

${\displaystyle u_{0}-v_{0}-v_{k}-\dotsb -v_{ak\equiv \pm b}-u_{\pm b}-u_{\pm (b-1)}-\dotsb -u_{\pm 1}-u_{0}}$

은 길이 ${\displaystyle a+b+2}$의 순환이다 (복부호 동순).

위 상계 가운데 적어도 하나가 포화된다. 즉, 만약 ${\displaystyle 1\leq k<n/2}$이며,

${\displaystyle k=\min \left\{1\leq k'<n/2\colon \operatorname {GPG} (n,k)\cong \operatorname {GPG} (n,k')\right\}}$

일 때, 일반화 페테르센 그래프 ${\displaystyle \operatorname {GPG} (n,k)}$의 안둘레는 다음 표에서, 위에서부터 가장 먼저 해당하는 행에 의해 주어진다.^{[4]:Theorem 2.8}

조건	안둘레
${\displaystyle n=3k}$	3
${\displaystyle n=4k}$	4
${\displaystyle k=1}$
${\displaystyle n=5k}$	5
${\displaystyle n=5k/2}$
${\displaystyle k=2}$
${\displaystyle n=6k}$	6
${\displaystyle k=3}$
${\displaystyle n=2k+2}$
${\displaystyle n=7k}$	7
${\displaystyle n=7k/2}$
${\displaystyle n=7k/3}$
${\displaystyle k=4}$
${\displaystyle n=2k+3}$
${\displaystyle n=3k\pm 2}$
그 밖의 경우	8

증명:

일반화 페테르센 그래프의 꼭짓점 및 변은

${\displaystyle \operatorname {V} (\operatorname {GPG} (n,k))=\{u_{i},v_{i}\colon i\in \mathbb {Z} /n\}}$

${\displaystyle \operatorname {E} (\operatorname {GPG} (n,k))=\{u_{i}u_{i+1},u_{i}v_{i},v_{i}v_{i+k}\colon i\in \mathbb {Z} /n\}}$

이다. 일반화 페테르센 그래프 속의 모든 순환은 당연히 짝수 개의 바큇살 ${\displaystyle u_{i}v_{i}}$을 포함한다.

모든 일반화 페테르센 그래프는 4개의 바큇살을 갖는 길이 8의 순환

${\displaystyle u_{0}-v_{0}-v_{k}-u_{k}-u_{k+1}-v_{k+1}-v_{1}-u_{1}-u_{0}}$

을 가지며, 바큇살 6개 이상의 순환의 길이는 항상 12 이상이다. 따라서, 2개의 바큇살 및 0개의 바큇살을 갖는 순환들만 고려하면 된다.

2개의 바큇살을 갖는 순환은 (편의상 첫 변을 ${\displaystyle u_{0}-u_{1}}$로 잡으면) 항상 다음과 같은 꼴이다.

${\displaystyle u_{0}-u_{1}-\dotsb -u_{b}-v_{b}-v_{b\pm k}-v_{b\pm 2k}-\dotsb -v_{b\pm ak}-u_{0}}$

이것이 존재하기 위해서는 ${\displaystyle ak\pm b\mid n}$이어야 하며, 이 경우 순환의 길이는 ${\displaystyle a+b+2}$이다.

• ${\displaystyle k}$가 최솟값이어야 하므로, ${\displaystyle ak+b=n}$ 및 ${\displaystyle ak+b=0}$인 경우만 고려해도 된다.
  • ${\displaystyle ak+b=0}$인 경우: ${\displaystyle (a,b)=(1,-k)}$인 경우가 최적이며, 이 경우 순환의 길이는 ${\displaystyle k+3}$이다.
  • ${\displaystyle ak+b=n}$인 경우:
    • 만약 ${\displaystyle n=ak\pm 1}$인 경우, ${\displaystyle \operatorname {GPG} (n,k)\cong \operatorname {GPG} (n,a)}$이다. 따라서, 이 경우 ${\displaystyle k}$는 최솟값을 갖지 못한다.
    • 만약 ${\displaystyle n=ak}$일 경우, 이 경우 0개의 바큇살을 갖는 길이 ${\displaystyle a}$의 순환이 더 짧다.
    • 만약 ${\displaystyle n=2k-b}$일 경우, ${\displaystyle k\geq n/2}$이다.
    • 위 경우를 제외하면, 이러한 순환의 길이가 8 미만인 경우는 남는 것은 ${\displaystyle (a,b)=(2,2),(2,3),(3,2),(3,-2)}$이다.

0개의 바큇살을 갖는 순환은 ${\displaystyle u_{i}}$ 또는 ${\displaystyle v_{i}}$로만 구성된다. ${\displaystyle u_{i}}$만으로 구성되는 유일한 순환의 길이는 ${\displaystyle n}$이며, ${\displaystyle v_{i}}$만으로 구성되는 순환의 길이는 ${\displaystyle n/\gcd\{n,k\}}$이다.

• 후자의 길이가 7 이하가 되려면, 가능한 경우는 ${\displaystyle n/k\in \{3/1,4/1,5/1,5/2,6/1,7/1,7/2,7/3\}}$이다.

케일리 그래프

나우루 그래프 ${\displaystyle \operatorname {GPG} (12,5)}$는 대칭군 ${\displaystyle \operatorname {Sym} (4)}$의 케일리 그래프이다.

일반화 페테르센 그래프 ${\displaystyle \operatorname {GPG} (n,k)}$에 대하여, 다음 두 조건이 서로 동치이다.^[5]

• 어떤 유한군의 케일리 그래프와 동형이다.
• ${\displaystyle k^{2}\equiv 1{\pmod {n}}}$

예를 들어, 나우루 그래프 ${\displaystyle \operatorname {GPG} (12,5)}$의 경우 ${\displaystyle 5^{2}\equiv 1{\pmod {12}}}$이며, 이는 대칭군 ${\displaystyle \operatorname {Sym} (4)}$의 케일리 그래프이다. 마찬가지로, 각기둥 그래프 ${\displaystyle \operatorname {GPG} (n,1)}$는 크기 ${\displaystyle 2n}$의 정이면체군 ${\displaystyle \operatorname {Dih} (n)}$의 케일리 그래프이다. 반면, 페테르센 그래프 ${\displaystyle \operatorname {GPG} (5,2)}$는 케일리 그래프가 아니다.

꼭짓점 색칠

일반화 페테르센 그래프는 삼차 그래프이므로, 브룩스 정리(영어: Brooks’ theorem)에 의하여 그 색칠수는 2 또는 3이다. 일반화 페테르센 그래프 ${\displaystyle \operatorname {GPG} (n,k)}$에 대하여, 다음 두 조건이 서로 동치이다.

• 이분 그래프이다. (즉, 색칠수가 2이다.)
• ${\displaystyle n}$이 짝수이며, ${\displaystyle k}$는 홀수이다.

다시 말해, 일반화 페테르센 그래프 ${\displaystyle \operatorname {GPG} (n,k)}$의 색칠수는 다음과 같다.

${\displaystyle \chi (\operatorname {GPG} (n,k))={\begin{cases}2&2\mid n\land 2\nmid k\\3&2\nmid n\lor 2\mid k\end{cases}}}$

여기서 ${\displaystyle \land }$는 논리곱(AND), ${\displaystyle \lor }$는 논리합(OR)이다. 예를 들어, 페테르센 그래프 ${\displaystyle \operatorname {GPG} (5,2)}$의 색칠수는 3이다.

• 
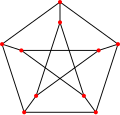
  페테르센 그래프 ${\displaystyle \operatorname {GPG} (5,2)}$의 3색 그래프 색칠
• 
  데자르그 그래프 ${\displaystyle \operatorname {GPG} (10,3)}$의 2색 그래프 색칠
• 
  뒤러 그래프 ${\displaystyle \operatorname {GPG} (6,2)}$의 3색 그래프 색칠

변 색칠

페테르센 그래프의 변 색칠수는 4이다.^[6] 페테르센 그래프는 변 색칠수가 4 이상인 가장 작은 삼차 그래프이다. 반면, 페테르센 그래프가 아닌 다른 모든 일반화 페테르센 그래프의 변 색칠수는 3이다.^[7]

일반화 페테르센 그래프 ${\displaystyle \operatorname {GPG} (9,2)}$는 (색들의 순열을 무시하면) 유일한 3색 변 색칠을 갖는다.

• 
  페테르센 그래프 ${\displaystyle \operatorname {GPG} (5,2)}$의 4색 변 색칠
• 
  뒤러 그래프 ${\displaystyle \operatorname {GPG} (6,2)}$의 3색 변 색칠
• 
  정십이면체 그래프 ${\displaystyle \operatorname {GPG} (10,2)}$의 3색 변 색칠
• 
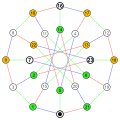
  데자르그 그래프 ${\displaystyle \operatorname {GPG} (10,3)}$의 3색 변 색칠
• 
  나우루 그래프 ${\displaystyle \operatorname {GPG} (12,5)}$의 3색 변 색칠

해밀턴 경로

임의의 일반화 페테르센 그래프 ${\displaystyle \operatorname {GPG} (n,k)}$ (${\displaystyle 3\leq n}$, ${\displaystyle 1\leq k<n/2}$)에 대하여, 다음 두 가지 가운데 정확히 하나가 성립한다.^[8]

• (가) 해밀턴 순환을 갖는다.
• (나) ${\displaystyle n\equiv 5{\pmod {6}}}$이며, ${\displaystyle k\in \{2,(n-1)/2\}}$이다.

또한, (나)의 경우, 임의의 꼭짓점을 제거하면 이는 해밀턴 순환을 갖는다. (특히, 모든 일반화 페테르센 그래프는 항상 해밀턴 경로를 갖는다.)

예를 들어, 페테르센 그래프 ${\displaystyle \operatorname {GPG} (5,2)}$는 해밀턴 경로를 가지지만, (나)의 경우에 해당하므로 해밀턴 순환을 가지지 못한다.

• 
  뒤러 그래프 ${\displaystyle \operatorname {GPG} (6,2)}$ 속의 해밀턴 순환. 맨 밖의 변들이 해밀턴 순환을 이룬다.
• 
  일반화 페테르센 그래프 ${\displaystyle \operatorname {GPG} (8,3)}$ 속의 해밀턴 순환. 맨 밖의 변들이 해밀턴 순환을 이룬다.
• 
  일반화 페테르센 그래프 ${\displaystyle \operatorname {GPG} (9,2)}$ 속의 해밀턴 순환. 해밀턴 순환에 속하는 변들은 굵게 칠해졌다.
• 
  정십이면체 그래프 ${\displaystyle \operatorname {GPG} (10,2)}$ 속의 해밀턴 순환. 해밀턴 순환에 속하는 변들은 붉은 색으로 굵게 칠해졌다.
• 
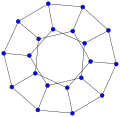
  나우루 그래프 ${\displaystyle \operatorname {GPG} (12,5)}$ 속의 해밀턴 순환. 맨 밖의 변들이 해밀턴 순환을 이룬다.

교차수

각기둥 그래프인 일반화 페테르센 그래프 ${\displaystyle \operatorname {GPG} (n,1)}$은 평면 그래프이다. 즉, 그래프 교차수가 0이다.

페테르센 그래프 ${\displaystyle \operatorname {GPG} (5,2)}$의 그래프 교차수는 2이다. 나우루 그래프 ${\displaystyle \operatorname {GPG} (12,5)}$의 그래프 교차수는 8이다. 특히, 이 두 그래프 둘 다 평면 그래프가 아니다.

평면 그래프가 아닌 모든 그래프는 완전 그래프 ${\displaystyle K_{5}}$ 또는 완전 이분 그래프 ${\displaystyle K_{3,3}}$를 그래프 마이너로 가지는데, 페테르센 그래프 ${\displaystyle \operatorname {GPG} (5,2)}$는 이 둘 다를 그래프 마이너로 갖는다.

• 
  오각기둥 그래프 ${\displaystyle \operatorname {GPG} (5,1)}$의 교차수는 0이다.
• 
  페테르센 그래프 ${\displaystyle \operatorname {GPG} (5,2)}$의 교차수는 2이다.
• 
  나우루 그래프 ${\displaystyle \operatorname {GPG} (12,5)}$의 교차수는 8이다.

예

일부 일반화 페테르센 그래프는 다음과 같은 특별한 이름을 갖는다.

• 페테르센 그래프는 일반화 페테르센 그래프 ${\displaystyle \operatorname {GPG} (5,2)}$이다. 이는 완전 그래프 ${\displaystyle K_{5}}$의 선 그래프의 여 그래프와 동형이다.
• 뒤러 그래프(영어: Dürer graph)는 일반화 페테르센 그래프 ${\displaystyle \operatorname {GPG} (6,2)}$이다.
• 일반화 페테르센 그래프 ${\displaystyle \operatorname {GPG} (10,2)}$는 정십이면체의 꼭짓점 및 변들로 구성된 그래프와 같다.
• 데자르그 그래프(영어: Desargues graph)는 일반화 페테르센 그래프 ${\displaystyle \operatorname {GPG} (10,3)}$이다.
• 일반화 페테르센 그래프 ${\displaystyle \operatorname {GPG} (n,1)}$는 ${\displaystyle n}$각형 각기둥의 꼭짓점 및 변들로 구성된 그래프와 같다.

• 
  일반화 페테르센 그래프 ${\displaystyle \operatorname {GPG} (3,1)}$
• 
  일반화 페테르센 그래프 (정육면체 그래프) ${\displaystyle \operatorname {GPG} (4,1)}$
• 
  일반화 페테르센 그래프 ${\displaystyle \operatorname {GPG} (5,1)}$
• 
  페테르센 그래프 ${\displaystyle \operatorname {GPG} (5,2)}$
• 
  일반화 페테르센 그래프 ${\displaystyle \operatorname {GPG} (6,1)}$
• 
  뒤러 그래프 ${\displaystyle \operatorname {GPG} (6,2)}$
• 
  일반화 페테르센 그래프 ${\displaystyle \operatorname {GPG} (7,1)}$
• 
  일반화 페테르센 그래프 ${\displaystyle \operatorname {GPG} (8,1)}$
• 
  정십이면체 그래프 ${\displaystyle \operatorname {GPG} (10,2)}$
• 
  데자르그 그래프 ${\displaystyle \operatorname {GPG} (10,3)}$
• 
  일반화 페테르센 그래프 ${\displaystyle \operatorname {GPG} (12,4)}$
• 
  나우루 그래프 ${\displaystyle \operatorname {GPG} (12,5)}$

역사

알브레히트 뒤러의 판화 《멜란콜리아 1》

데자르그의 정리에 등장하는 작도. 10개의 점 ${\displaystyle (A,B,C,A',B',C',P,Q,R,S)}$와 10개의 직선 ${\displaystyle (a,b,c,a',b',c',p,q,r,s)}$에 각각 어떤 그래프의 꼭짓점을 대응시키고, 인접하는 점과 직선에 대응하는 두 꼭짓점 사이를 변으로 이으면, 데자르그 그래프 ${\displaystyle \operatorname {GPG} (10,3)}$를 얻는다.

나우루의 국기

독일의 판화가 알브레히트 뒤러의 1514년 판화 《멜란콜리아 1》(독일어: Melancholia Ⅰ)에는 다면체가 등장하는데, 그 꼭짓점과 변으로 구성된 그래프는 뒤러 그래프이다.

1898년에 덴마크의 수학자 율리우스 페테르센이 이 그래프를 다룬 3쪽의 논문을 출판하였으며,^{[9]:227, Fig. 5} 이로부터 명명되었다. 페테르센은 이 그래프를 다음과 같은 (잘못된) 추측에 대한 반례로 제시하였다.

연결 삼차 그래프 가운데, 임의의 변을 제거하더라도 연결 그래프로 남는 것들의 경우, 모두 변 색칠수가 3 이하이다.

“데자르그 그래프”라는 이름은 프랑스의 수학자 지라르 데자르그의 이름을 딴 것이다. 데자르그가 연구한 사영기하학의 한 정리에서 등장하는 작도에서, 각 직선과 각 점에 그래프 꼭짓점을 대응시키며, 서로 인접하는 점과 직선(에 대응하는 두 꼭짓점) 사이를 변으로 이으면, 이는 데자르그 그래프가 된다.

해럴드 스콧 맥도널드 콕서터는 1950년에 일반화 페테르센 그래프를 도입하였다.^{[10]:418, §2} 콕서터는 일반화 페테르센 그래프 ${\displaystyle \operatorname {GPG} (n,k)}$를 ${\displaystyle \{n\}+\{n/k\}}$로 표기하였으며, 이에 특별한 이름을 부여하지 않았다.

1969년에 마크 왓킨스(영어: Mark E. Watkins)가 이 그래프 족을 “일반화 페테르센 그래프”(영어: generalized Petersen graph)라고 명명하였다.^[11]

“나우루 그래프”(영어: Nauru graph)라는 이름은 데이비드 아서 엡스타인(영어: David Arthur Eppstein)이 도입하였으며, 이 그래프의 구성에 등장하는 12각 별 모양이 나우루의 국기에 등장하는 별과 흡사하기 때문에 붙여졌다.