상위 질문
타임라인
채팅
관점
멱집합
위키백과, 무료 백과사전
Remove ads
집합론에서 멱집합(冪集合, 영어: power set)은 주어진 집합의 모든 부분 집합들로 구성된 집합이다.

정의
요약
관점
집합 의 멱집합 또는 는 의 모든 부분 집합들로 구성된 집합이다. 즉, 이는 다음과 같다.
선택 공리를 추가한 체르멜로-프렝켈 집합론(ZFC)의 멱집합 공리(영어: axiom of power set)는 다음과 같은 명제이다.
- 임의의 집합 에 대하여, 다음 조건을 만족시키는 집합 가 존재한다.
- 임의의 집합 에 대하여, 만약 (임의의 에 대하여 )라면, 이다.
이는 ZFC의 공리이며, 특히 참이다. 멱집합 공리 및 다른 ZFC 공리들로부터, 임의의 집합 의 멱집합의 존재를 다음과 같이 증명할 수 있다. 위 조건을 만족시키는 집합 를 잡자. 그렇다면, 분류 공리꼴에 따라, 다음과 같은 집합을 정의할 수 있다.
또한, 의 선택에 따라, 는 의 멱집합을 이룬다. 확장 공리에 따라, 임의의 집합의 멱집합은 유일하다.
Remove ads
성질
요약
관점
크기
집합 의 멱집합 의 크기는
이다. 여기서 는 의 크기를 나타내며, 는 기수의 거듭제곱을 나타낸다. 만약 가 유한 집합일 경우, 는 (의 원소 개수를 나타내는) 자연수이며, 기수의 거듭제곱 연산은 자연수의 거듭제곱 연산과 일치한다. 특히, 유한 집합의 멱집합은 유한 집합이다.
다음과 같은 부등식이 성립한다.
여기서 는 보다 큰 최소의 기수이다 (선택 공리를 가정하면 이는 항상 존재한다). 이를 칸토어 정리라고 한다. 이에 따라, 멱집합 의 크기는 항상 원래 집합 의 크기보다 크다. 특히, 가 가산 무한 집합인 경우 이다. 명제 는 연속체 가설이라고 부른다. 연속체 가설과 그 부정 모두 ZFC에서 증명할 수 없다.
순서론적 성질
집합 의 멱집합은 부분 집합 관계에 대하여 완비 불 대수 를 이룬다. 최소 원소는 공집합 , 최대 원소는 원래의 집합 , 이음은 합집합 , 만남은 교집합 이다. 또한, 임의의 부분 집합 의 상한은 합집합
으로 주어지며, 하한은 교집합
으로 주어진다 ().
함자성
를 이룬다.
Remove ads
예
요약
관점
공집합의 멱집합은 공집합을 원소로 가지는 한원소 집합이다.
한원소 집합 은 공집합과 자기 자신을 부분 집합으로 하므로 그 멱집합은
이다.
두원소 집합 의 부분 집합들은 정확히 다음과 같다.
따라서 그 멱집합은
이다.
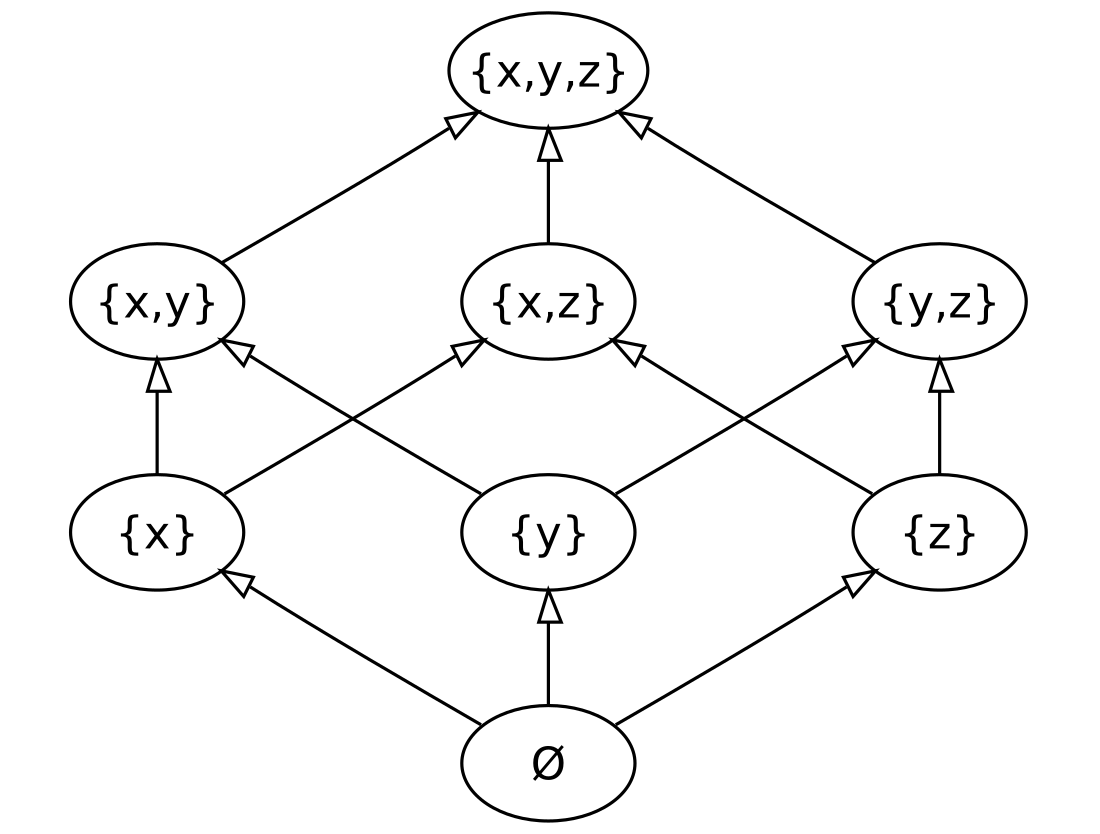
세원소 집합 의 부분 집합들은 정확히 다음과 같다.
따라서 그 멱집합은
이다.
Remove ads
같이 보기
외부 링크
- 수학사랑 Q & A (멱집합)
- “Power set”. 《Encyclopedia of Mathematics》 (영어). Springer-Verlag. 2001. ISBN 978-1-55608-010-4.
- Weisstein, Eric Wolfgang. “Axiom of the power set”. 《Wolfram MathWorld》 (영어). Wolfram Research.
- “Power set”. 《nLab》 (영어).
- “Power set”. 《PlanetMath》 (영어).
- “Axiom of power set”. 《PlanetMath》 (영어).
- “Definition: power set”. 《ProofWiki》 (영어).
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads