배열

다른 뜻에 대해서는 배열 (동음이의) 문서를 참고하십시오.

컴퓨터 과학에서 배열(영어: array, 配列·排列, 문화어: 배렬)은 동일한 메모리 크기의 요소(즉, 값 또는 변수) 모음으로 구성된 자료 구조이며, 각 요소는 하나 이상의 배열 색인 또는 키로 식별된다. 이러한 색인 또는 키의 모음은 색인 튜플로 알려진 튜플일 수 있다. 일반적으로 배열은 동일한 자료형을 가진 변경 가능하고 선형적인 요소 모음이다. 배열은 각 요소의 위치(메모리 주소)가 수학 공식에 의해 색인 튜플로부터 계산될 수 있도록 저장된다.^[1][2][3] 가장 간단한 자료 구조 유형은 1차원 배열이라고도 하는 선형 배열이다.

예를 들어, 색인이 0부터 9까지인 10개의 32비트 (4바이트) 정수 변수 배열은 메모리 주소 2000, 2004, 2008, ..., 2036 ( 십육진법: 0x7D0, 0x7D4, 0x7D8, ..., 0x7F4)에 10개의 워드로 저장될 수 있으며, 색인 i를 가진 요소는 주소 2000 + (i × 4)를 갖는다.^[4] 배열의 첫 번째 요소의 메모리 주소를 첫 번째 주소, 기초 주소 또는 기준 주소라고 한다.

행렬의 수학적 개념이 2차원 그리드로 표현될 수 있기 때문에, 2차원 배열은 때때로 "행렬"이라고도 불린다. 어떤 경우에는 "벡터"라는 용어가 컴퓨터에서 배열을 지칭하는 데 사용되지만, 벡터보다는 튜플이 수학적으로 더 정확한 등가물이다. 표는 특히 순람표의 형태로 종종 배열로 구현되며, "표"라는 단어는 때때로 배열의 동의어로 사용된다.

배열은 가장 오래되고 중요한 자료 구조 중 하나이며 거의 모든 프로그램에서 사용된다. 또한 리스트 및 문자열과 같은 많은 다른 자료 구조를 구현하는 데 사용된다. 이는 컴퓨터의 주소 지정 논리를 효과적으로 활용한다. 대부분의 현대 컴퓨터와 많은 외부 저장 장치에서 메모리는 워드의 1차원 배열이며, 그 색인은 주소이다. 프로세서, 특히 벡터 프로세서는 종종 배열 연산에 최적화되어 있다.

배열은 요소 색인이 실행 시간에 계산될 수 있기 때문에 주로 유용하다. 특히, 이 기능은 단일 반복 문이 배열의 임의의 많은 요소를 처리할 수 있도록 한다. 이 때문에 배열 자료 구조의 요소는 동일한 크기를 가져야 하며 동일한 자료 표현을 사용해야 한다. 유효한 색인 튜플의 집합과 요소의 주소(따라서 요소 주소 지정 공식)는 일반적으로^[3][5] 배열이 사용되는 동안 고정되지만^[2] 항상 그런 것은 아니다.

"배열"이라는 용어는 대부분의 고급 프로그래밍 언어에서 제공하는 자료형의 일종인 배열 자료형을 지칭할 수도 있는데, 이는 실행 시간에 하나 이상의 색인으로 선택할 수 있는 값 또는 변수 모음으로 구성된다. 배열 자료형은 종종 배열 구조로 구현된다. 그러나 일부 언어에서는 해시 테이블, 연결 리스트, 탐색 트리 또는 다른 자료 구조로 구현될 수 있다.

이 용어는 특히 알고리즘 설명에서 연관 배열 또는 "추상 배열"을 의미하는 데 사용되기도 하는데, 이는 배열의 본질적인 속성을 포착하기 위한 이론 컴퓨터 과학 모델(즉, 추상 자료형 또는 ADT)이다.

역사

최초의 디지털 컴퓨터는 자료 테이블, 벡터 및 행렬 계산, 그리고 다른 여러 목적을 위해 배열 구조를 설정하고 접근하기 위해 기계어 프로그래밍을 사용했다. 존 폰 노이만은 1945년 최초의 프로그램 내장형 컴퓨터를 구축하는 동안 최초의 배열 정렬 프로그램(합병 정렬)을 작성했다.^[6] 배열 색인 지정은 원래 자체 수정 코드로 이루어졌고, 나중에는 인덱스 레지스터와 간접 주소 지정을 사용했다. 1960년대에 설계된 일부 메인프레임(예: 버로스 B5000 및 그 후속 모델)은 하드웨어에서 인덱스 경계 검사를 수행하기 위해 메모리 세그먼트를 사용했다.^[7]

어셈블리어는 기계 자체가 제공하는 것 외에 배열에 대한 특별한 지원이 거의 없다. FORTRAN (1957), 리스프 (1958), 코볼 (1960), ALGOL 60 (1960)을 포함한 초창기 고급 프로그래밍 언어들은 다차원 배열을 지원했고, C (1972)도 그러했다. C++ (1983)에서는 실행 시간에 차원이 고정되는 다차원 배열^[3][5]뿐만 아니라 실행 시간에 유연한 배열^[2]을 위한 클래스 템플릿이 존재한다.

응용

배열은 수학적 벡터 및 행렬뿐만 아니라 다른 종류의 직사각형 표를 구현하는 데 사용된다. 크고 작은 많은 데이터베이스는 요소가 레코드인 1차원 배열로 구성되거나 이를 포함한다.

배열은 리스트, 힙, 해시 테이블, 덱, 큐, 스택, 문자열, VLists와 같은 다른 자료 구조를 구현하는 데 사용된다. 다른 자료 구조의 배열 기반 구현은 종종 간단하고 공간 효율적이며 (암묵적 자료 구조s), 오버헤드가 거의 필요하지 않지만, 트리 기반 자료 구조와 비교할 때 특히 수정될 때 공간 복잡성이 좋지 않을 수 있다( 정렬된 배열을 탐색 트리와 비교).

하나 이상의 큰 배열은 때때로 프로그램 내에서 동적 메모리 할당, 특히 메모리 풀 할당을 에뮬레이션하는 데 사용된다. 역사적으로 이것이 "동적 메모리"를 이식성 있게 할당하는 유일한 방법이었던 경우가 있다.

배열은 프로그램에서 부분적 또는 완전한 제어 흐름을 결정하는 데 사용될 수 있으며, (그렇지 않으면 반복적인) 여러 IF 문의 압축된 대안으로 사용된다. 이 맥락에서 배열은 제어테이블이라고 불리며, 배열에 포함된 값에 따라 제어 흐름이 변경되는 전용 인터프리터와 함께 사용된다. 배열은 프로그램 실행 경로를 지시하는 서브루틴 포인터 (또는 SWITCH 문에서 작동할 수 있는 상대 서브루틴 번호)를 포함할 수 있다.

요소 식별자와 주소 지정 공식

데이터 객체가 배열에 저장될 때, 개별 객체는 일반적으로 음수가 아닌 스칼라 정수인 인덱스로 선택된다. 인덱스는 아래첨자라고도 한다. 인덱스는 배열 값을 저장된 객체에 매핑한다.

배열 요소에 인덱스를 지정하는 세 가지 방법이 있다.

0 (0-기반 인덱싱)

배열의 첫 번째 요소는 아래첨자 0으로 인덱스된다.^[8]

1 (1-기반 인덱싱)

배열의 첫 번째 요소는 아래첨자 1로 인덱스된다.

n (n-기반 인덱싱)

배열의 기본 인덱스는 자유롭게 선택할 수 있다. 일반적으로 n-기반 인덱싱을 허용하는 프로그래밍 언어는 음수 인덱스 값과 열거형 또는 문자와 같은 다른 스칼라 자료형을 배열 인덱스로 사용할 수 있도록 한다.

0-기반 인덱싱을 사용하는 것은 C, Java, 리스프를 포함한 많은 영향력 있는 프로그래밍 언어의 설계 선택이다. 이는 아래첨자가 배열의 시작 위치로부터의 오프셋을 참조하므로 첫 번째 요소의 오프셋이 0이 되는 더 간단한 구현으로 이어진다.

배열은 여러 차원을 가질 수 있으므로 여러 인덱스를 사용하여 배열에 접근하는 것은 드문 일이 아니다. 예를 들어, 3개의 행과 4개의 열을 가진 2차원 배열 A는 0-기반 인덱싱 시스템의 경우 A[1][3] 표현식으로 2번째 행과 4번째 열의 요소에 접근할 수 있다. 따라서 2차원 배열에는 두 개의 인덱스가, 3차원 배열에는 세 개의 인덱스가, n차원 배열에는 n개의 인덱스가 사용된다.

요소를 지정하는 데 필요한 인덱스의 수를 배열의 차원, 차원성 또는 순위라고 한다.

표준 배열에서 각 인덱스는 연속적인 정수 (또는 일부 열거형의 연속적인 값)의 특정 범위로 제한되며, 요소의 주소는 인덱스에 대한 "선형" 공식으로 계산된다.

1차원 배열

일반적인 1차원 배열 다이어그램

1차원 배열(또는 단일 차원 배열)은 선형 배열의 한 종류이다. 요소에 접근하는 것은 행 또는 열 인덱스를 나타낼 수 있는 단일 아래첨자를 포함한다.

예를 들어, 10개의 정수를 저장하는 a라는 1차원 배열을 선언하는 C 선언 int a[10];를 고려해 보자. 여기에서 배열은 int 유형의 10개 요소를 저장할 수 있다. 이 배열은 0부터 9까지의 인덱스를 갖는다. 예를 들어, a[0]과 a[9]는 각각 첫 번째 요소와 마지막 요소이다.

선형 주소 지정이 있는 벡터의 경우, 인덱스 i를 가진 요소는 B + c · i 주소에 위치하며, 여기서 B는 고정된 기준 주소이고 c는 주소 증분 또는 스트라이드라고도 하는 고정 상수이다.

유효한 요소 인덱스가 0에서 시작하는 경우, 상수 B는 단순히 배열의 첫 번째 요소의 주소이다. 이러한 이유로 C 프로그래밍 언어는 배열 인덱스가 항상 0에서 시작하도록 지정하며, 많은 프로그래머는 그 요소를 "첫 번째"가 아닌 "영번째"라고 부른다.

그러나 기준 주소 B를 적절하게 선택함으로써 첫 번째 요소의 인덱스를 선택할 수 있다. 예를 들어, 배열에 1부터 5까지 인덱스된 다섯 개의 요소가 있고 기준 주소 B가 B + 30c로 대체되면, 이들 요소의 인덱스는 31부터 35까지가 된다. 번호 매김이 0에서 시작하지 않으면 상수 B는 어떤 요소의 주소도 아닐 수 있다.

일반적인 2차원 배열 다이어그램

다차원 배열

일반적인 3차원 배열 다이어그램

다차원 배열의 경우, 인덱스 i,j를 가진 요소는 B + c · i + d · j 주소를 가지며, 여기서 계수 c와 d는 각각 행 및 열 주소 증분이다.

더 일반적으로, k차원 배열에서 인덱스 i₁, i₂, ..., i_k를 가진 요소의 주소는

B + c₁ · i₁ + c₂ · i₂ + … + c_k · i_k.

예를 들어: int a[2][3];

이는 배열 a가 2개의 행과 3개의 열을 가지며, 배열이 정수형임을 의미한다. 여기에는 6개의 요소를 저장할 수 있으며, 이들은 선형으로 저장되지만 첫 번째 행에서 시작하여 선형으로 저장된 다음 두 번째 행으로 계속된다. 위의 배열은 a₁₁, a₁₂, a₁₃, a₂₁, a₂₂, a₂₃로 저장된다.

이 공식은 메모리에 들어갈 수 있는 모든 배열에 대해 k개의 곱셈과 k개의 덧셈만 필요하다. 게다가, 어떤 계수가 2의 고정된 거듭제곱이면, 곱셈은 비트 시프트로 대체될 수 있다.

계수 c_k는 모든 유효한 인덱스 튜플이 서로 다른 요소의 주소에 매핑되도록 선택되어야 한다.

각 인덱스의 최소 유효 값이 0인 경우, B는 모든 인덱스가 0인 요소의 주소이다. 1차원 경우와 마찬가지로, 기본 주소 B를 변경하여 요소 인덱스를 변경할 수 있다. 따라서 2차원 배열의 행과 열이 각각 1부터 10과 1부터 20까지 인덱스된다면, B를 B + c₁ − 3c₂로 대체하면 각각 0부터 9와 4부터 23까지로 다시 번호가 매겨진다. 이 기능을 활용하여 일부 언어(예: FORTRAN 77)는 수학적 전통에 따라 배열 인덱스가 1에서 시작하도록 지정하는 반면, 다른 언어(예: Fortran 90, Pascal 및 Algol)는 사용자가 각 인덱스의 최소값을 선택할 수 있도록 한다.

도프 벡터

 이 부분의 본문은 도프 벡터입니다.

주소 지정 공식은 차원 d, 기본 주소 B, 그리고 증분 c₁, c₂, ..., c_k에 의해 완전히 정의된다. 이 매개변수들을 배열의 디스크립터, 스트라이드 벡터 또는 도프 벡터라고 불리는 레코드로 묶는 것이 종종 유용하다.^[2][3] 각 요소의 크기와 각 인덱스에 허용되는 최소 및 최대 값도 도프 벡터에 포함될 수 있다. 도프 벡터는 배열에 대한 완전한 핸들이며, 배열을 프로시저의 인수로 전달하는 편리한 방법이다. 많은 유용한 배열 슬라이싱 작업(예: 서브 배열 선택, 인덱스 교환 또는 인덱스 방향 반전)은 도프 벡터를 조작하여 매우 효율적으로 수행할 수 있다.^[2]

컴팩트한 배치

 이 부분의 본문은 행 우선 순서와 열 우선 순서입니다.

종종 계수는 요소들이 연속적인 메모리 영역을 차지하도록 선택된다. 그러나 이는 필수는 아니다. 배열이 항상 연속적인 요소로 생성된다 하더라도, 일부 배열 슬라이싱 작업은 비연속적인 서브 배열을 생성할 수 있다.

행 우선 순서와 열 우선 순서의 그림

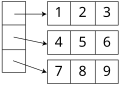
2차원 배열에 대한 두 가지 체계적인 컴팩트한 배치 방식이 있다. 예를 들어, 다음 행렬을 고려해 보자.

${\displaystyle A={\begin{bmatrix}1&2&3\\4&5&6\\7&8&9\end{bmatrix}}.}$

행 우선 순서 배치(C에서 정적으로 선언된 배열에 채택됨)에서는 각 행의 요소가 연속적인 위치에 저장되며, 한 행의 모든 요소는 다음 행의 어떤 요소보다 낮은 주소를 갖는다.

1

2

3

4

5

6

7

8

9

열 우선 순서(전통적으로 포트란에서 사용됨)에서는 각 열의 요소가 메모리에서 연속적이며, 한 열의 모든 요소는 다음 열의 어떤 요소보다 낮은 주소를 갖는다.

1

4

7

2

5

8

3

6

9

3개 이상의 인덱스를 가진 배열의 경우, "행 우선 순서"는 마지막 인덱스에서만 1만큼 다른 인덱스 튜플을 가진 두 요소를 연속적인 위치에 놓는다. "열 우선 순서"는 첫 번째 인덱스에 대해 유사하다.

프로세서 캐시 또는 가상 메모리를 사용하는 시스템에서 배열을 스캔하는 것은 연속적인 요소가 메모리의 연속적인 위치에 저장될 때, 드문드문 흩어져 있는 경우보다 훨씬 빠르다. 이를 공간 지역성이라고 하며, 참조 국부성의 한 유형이다. 다차원 배열을 사용하는 많은 알고리즘은 예측 가능한 순서로 배열을 스캔할 것이다. 프로그래머(또는 정교한 컴파일러)는 이 정보를 사용하여 각 배열에 대해 행 우선 또는 열 우선 배치를 선택할 수 있다. 예를 들어, 두 행렬 A·B의 곱을 계산할 때 A는 행 우선 순서로, B는 열 우선 순서로 저장하는 것이 가장 좋다.

크기 변경

 이 부분의 본문은 동적 배열입니다.

정적 배열은 생성 시 크기가 고정되어 있어 요소를 삽입하거나 제거할 수 없다. 그러나 새 배열을 할당하고 이전 배열의 내용을 복사함으로써 배열의 동적 버전을 효과적으로 구현할 수 있다. 자세한 내용은 동적 배열을 참조하라. 이 작업이 드물게 수행된다면, 배열 끝에 삽입하는 데에는 상환된 상수 시간만 필요하다.

일부 배열 자료 구조는 저장 공간을 재할당하지 않지만, 사용 중인 배열 요소의 수를 저장하는 카운트 또는 크기를 저장한다. 이는 효과적으로 배열을 고정된 최대 크기 또는 용량을 가진 동적 배열로 만든다. 파스칼 문자열이 그 예이다.

비선형 공식

더 복잡한(비선형) 공식이 때때로 사용된다. 예를 들어, 컴팩트한 2차원 삼각형 배열의 경우, 주소 지정 공식은 2차 다항식이다.

효율성

저장 및 선택 모두 (결정론적 최악의 경우) 상수 시간이 걸린다. 배열은 보유하는 요소 n의 수에 대해 선형 (O(n)) 공간을 차지한다.

요소 크기가 k이고 캐시 라인 크기가 B바이트인 기계에서, n개 요소 배열을 반복하는 데는 최소 ceiling(nk/B)의 캐시 미스가 필요하다. 왜냐하면 요소들이 연속적인 메모리 위치를 차지하기 때문이다. 이는 임의의 메모리 위치에 있는 n개 요소에 접근하는 데 필요한 캐시 미스 수보다 약 B/k배 더 좋다. 결과적으로, 배열에 대한 순차적 반복은 실제로 다른 많은 자료 구조에 대한 반복보다 현저히 빠르며, 이를 참조 국부성이라는 속성이라고 한다 (그러나 완전 해시 또는 동일한 (지역) 배열 내에서 자명한 해시를 사용하는 것이 훨씬 빠르지 않다는 의미는 아니다 - 그리고 상수 시간에 달성 가능하다). 라이브러리는 memcpy와 같은 메모리 범위 복사를 위한 저수준 최적화된 기능을 제공하며, 이는 개별 요소 접근을 통해 달성할 수 있는 것보다 훨씬 빠르게 연속적인 배열 요소 블록을 이동하는 데 사용될 수 있다. 이러한 최적화된 루틴의 속도 향상은 배열 요소 크기, 아키텍처 및 구현에 따라 달라진다.

메모리 측면에서 배열은 요소당 오버헤드가 없는 컴팩트한 자료 구조이다. 배열당 오버헤드(예: 인덱스 경계 저장)가 있을 수 있지만 이는 언어에 따라 다르다. 또한 여러 배열 요소를 단일 워드에 저장할 수 있으므로 배열에 저장된 요소가 개별 변수에 저장된 동일한 요소보다 적은 메모리를 필요로 할 수 있다. 이러한 배열은 종종 팩킹 배열이라고 불린다. 극단적이지만 일반적으로 사용되는 경우는 비트 배열이며, 여기서 각 비트는 단일 요소를 나타낸다. 따라서 단일 옥텟은 가장 컴팩트한 형태로 최대 8가지 다른 조건의 최대 256가지 다른 조합을 저장할 수 있다.

정적으로 예측 가능한 접근 패턴을 가진 배열 접근은 데이터 병렬성의 주요 원천이다.

다른 자료 구조와의 비교

틀:자료 구조 비교 목록 동적 배열 또는 확장 가능한 배열은 배열과 유사하지만 요소를 삽입하고 삭제하는 기능을 추가한다. 특히 끝에서의 추가 및 삭제가 효율적이다. 그러나 배열은 추가 저장 공간을 예약하지 않는 반면, 이들은 선형 (Θ(n))의 추가 저장 공간을 예약한다.

연관 배열은 인덱스 값이 희소할 때 막대한 저장 공간 오버헤드 없이 배열과 유사한 기능을 제공하는 메커니즘을 제공한다. 예를 들어, 인덱스 1과 20억에만 값을 포함하는 배열은 이러한 구조를 사용하는 이점을 얻을 수 있다. 정수 키를 가진 특수화된 연관 배열에는 패트리샤 트라이, 주디 배열, 판 엠데 보아스 트리가 포함된다.

균형 트리는 색인 접근에 O(log n) 시간이 필요하지만, O(log n) 시간에 요소를 삽입하거나 삭제할 수도 있다.^[9] 반면, 확장 가능한 배열은 임의의 위치에 요소를 삽입하거나 삭제하는 데 선형 (Θ(n)) 시간이 필요하다.

연결 리스트는 중간에서 상수 시간 제거 및 삽입을 허용하지만, 색인 접근에는 선형 시간이 걸린다. 메모리 사용량은 일반적으로 배열보다 나쁘지만 여전히 선형이다.

1차원 배열들의 1차원 배열(행)로 저장된 2차원 배열.

일리프 벡터는 다차원 배열 구조의 대안이다. 이는 1차원보다 차원이 낮은 배열에 대한 참조의 1차원 배열을 사용한다. 특히 2차원의 경우, 이 대안 구조는 행당 벡터에 대한 포인터(C 또는 C++의 포인터)의 벡터가 될 것이다. 따라서 배열 A의 i행 j열에 있는 요소는 이중 인덱싱(일반적인 표기법에서 A[i][j])으로 접근된다. 이 대안 구조는 들쭉날쭉한 배열을 허용하며, 각 행은 다른 크기를 가질 수 있다. 또는 일반적으로 각 인덱스의 유효 범위는 모든 선행 인덱스의 값에 따라 달라진다. 또한 (열 주소 증분에 의한) 곱셈 하나를 비트 시프트(행 포인터 벡터를 인덱싱하기 위한)와 하나의 추가 메모리 접근(행 주소 가져오기)으로 대체하여 절약하며, 이는 일부 아키텍처에서 가치가 있을 수 있다.

차원

배열의 차원은 요소를 선택하는 데 필요한 인덱스의 수이다. 따라서 배열을 가능한 인덱스 조합 집합에 대한 함수로 볼 때, 그 영역이 이산 부분 집합인 공간의 차원이다. 따라서 1차원 배열은 자료의 리스트이고, 2차원 배열은 자료의 직사각형이며,^[10] 3차원 배열은 자료의 블록 등이다.

이는 주어진 영역을 가진 모든 행렬 집합의 차원, 즉 배열의 요소 수와 혼동해서는 안 된다. 예를 들어, 5개의 행과 4개의 열을 가진 배열은 2차원이지만, 이러한 행렬은 20차원 공간을 형성한다. 마찬가지로, 3차원 벡터는 크기가 3인 1차원 배열로 표현될 수 있다.

같이 보기

• 동적 배열
• 병렬 배열
• 가변 길이 배열
• 비트 배열
• 연결 리스트
• 문자열