정역

다른 뜻에 대해서는 정역 (동음이의) 문서를 참고하십시오.

가환대수학에서 정역(整域, 영어: integral domain)은 영인자가 존재하지 않는, 자명환이 아닌 가환환이다. 정역은 정수환의 일반화이며, 0이 아닌 원소의 역원을 추가하여 분수체를 만들 수 있다.

정의

임의의 환 ${\displaystyle R}$의 원소 ${\displaystyle r\in R}$에 대하여, ${\displaystyle (r\cdot )\colon R\to R,\;s\mapsto rs}$가 단사 함수일 경우 ${\displaystyle r}$를 정칙원(正則元素, 영어: regular element)이라고 한다.

(곱셈 항등원을 갖는) 가환환 ${\displaystyle R}$에 대하여, 다음 조건들이 서로 동치이며, 이를 만족시키는 가환환을 정역이라고 한다.

• ${\displaystyle R}$는 다음 두 조건을 만족시킨다.
  • (영인자의 부재) 모든 ${\displaystyle a,b\in R\setminus \{0\}}$에 대하여, ${\displaystyle ab\neq 0}$이다.
  • (비자명성) ${\displaystyle R}$는 자명환이 아니다. 즉, ${\displaystyle 1\neq 0}$이다.
• ${\displaystyle R\setminus \{0\}}$이 곱셈에 대하여 (공집합이 아닌) 가환 모노이드를 이룬다.
• ${\displaystyle R}$의 영 아이디얼이 소 아이디얼이다.
• ${\displaystyle R}$는 체의 부분환과 동형이다.
• ${\displaystyle R}$는 자명환이 아니며, ${\displaystyle R}$의 0이 아닌 모든 원소가 정칙원이다.

스킴 ${\displaystyle X}$에 대하여, 다음 두 조건이 서로 동치이며, 이를 만족시키는 스킴을 정역 스킴(整域scheme, 영어: integral scheme, 프랑스어: schéma intègre)이라고 한다.

• ${\displaystyle X}$는 공집합이 아니며, 공집합이 아닌 모든 아핀 열린집합 ${\displaystyle U}$에 대하여 ${\displaystyle \Gamma (U;{\mathcal {O}}_{X})}$는 정역이다.^[1]:82
• ${\displaystyle X}$는 축소 스킴이며 기약 스킴이다.^{[1]:82, Proposition II.3.1}
• ${\displaystyle X}$는 공집합이 아니며, 모든 ${\displaystyle x\in X}$에 대하여 줄기 ${\displaystyle {\mathcal {O}}_{X,x}}$가 정역이며, ${\displaystyle X}$는 연결 공간이다.^{[2]:66, Exercise 2.4.4}

성질

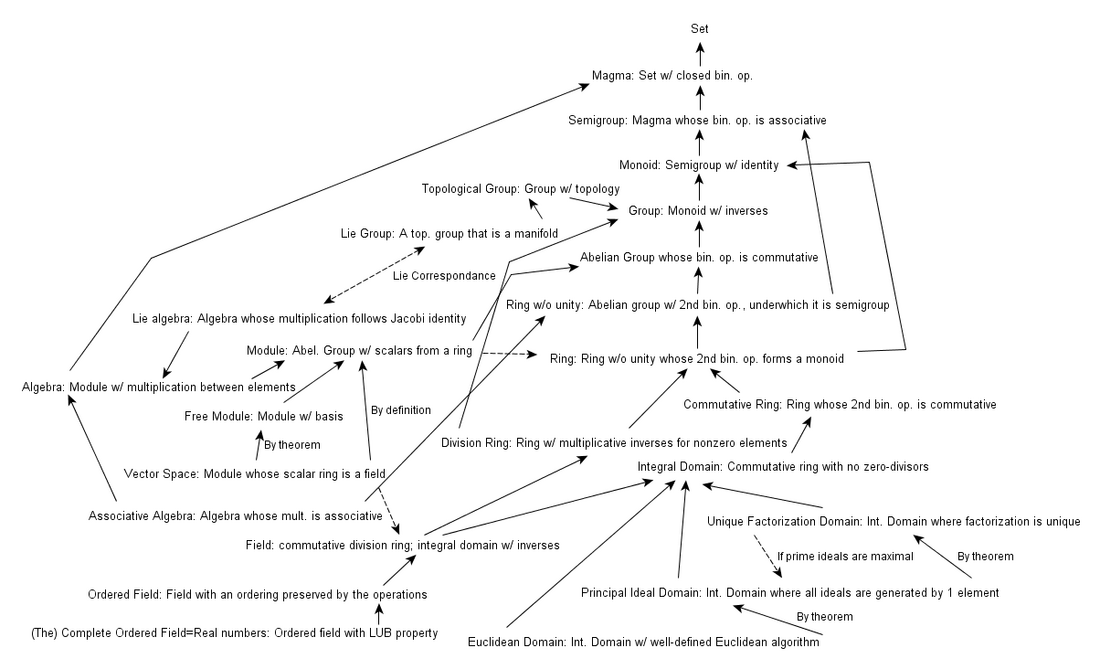
다음과 같은 포함 관계가 성립한다.

가환환 ⊋ 정역 ⊋ 정수적으로 닫힌 정역 ⊋ 크룰 정역 ⊋ 유일 인수 분해 정역 ∪ 데데킨트 정역 ⊋ 유일 인수 분해 정역 ∩ 데데킨트 정역 = 주 아이디얼 정역 ⊋ 유클리드 정역 ⊋ 체

정역의 환의 표수는 0이거나 아니면 소수이다. 양의 표수 ${\displaystyle p>0}$의 정역의 경우, 프로베니우스 사상 ${\displaystyle x\mapsto x^{p}}$은 단사 함수이다.

정역의 경우, 항상 분수체를 취할 수 있다.

가환환 ${\displaystyle R}$ 및 아이디얼 ${\displaystyle {\mathfrak {a}}\subset R}$에 대하여, 다음 두 조건이 서로 동치이다.

• ${\displaystyle {\mathfrak {a}}}$가 소 아이디얼이다.
• ${\displaystyle R/{\mathfrak {a}}}$가 정역이다.

정역의 귀납적 극한은 역시 정역이다.

가환환 ${\displaystyle R}$에 대하여, 다음 두 조건이 서로 동치이다.^{[1]:82, Example II.3.0.1[2]:65}

• ${\displaystyle R}$는 정역이다.
• 아핀 스킴 ${\displaystyle \operatorname {Spec} R}$는 정역 스킴이다.

웨더번 정리에 따르면, 모든 유한 정역은 유한체이다.

예

정수환 ${\displaystyle \mathbb {Z} }$은 정역을 이룬다. 모든 체는 정역을 이룬다. 모든 대수적 수체의 대수적 정수환 ${\displaystyle {\mathcal {O}}_{K}}$은 (데데킨트) 정역이다.

정수환의 몫환 ${\displaystyle \mathbb {Z} /(n^{2})}$의 경우, ${\displaystyle n\neq 0}$이지만 ${\displaystyle n\cdot n=0}$이므로 정역이 아니다.

모든 대수다양체는 정역 스킴이다.

같이 보기

• 영역 (환론)
• 소환 (환론)
• 분수체
• 영인자