해밀턴 경로

그래프 이론에서 해밀턴 경로(Hamilton經路, 영어: Hamiltonian path)는 모든 꼭짓점을 한 번씩 지나는 경로이다.

굵은 글씨

정십이면체의 모든 꼭짓점을 지나는 해밀턴 순환

8*8 그리드 그래프의 세 가지 예

정의

그래프 ${\displaystyle G}$의 해밀턴 경로 ${\displaystyle p}$는 ${\displaystyle G}$의 모든 꼭짓점을 포함하는 경로이다. (정의에 따라, 경로는 꼭짓점을 중복하여 거치지 않는 보행이다.) 해밀턴 순환(영어: Hamiltonian cycle)은 해밀턴 경로인 순환이다.

해밀턴 순환을 갖는 그래프를 해밀턴 그래프(영어: Hamiltonian graph)라고 한다. 해밀턴 경로를 갖는 그래프를 자취 존재 그래프(영어: traceable graph)라고 한다.

성질

유한 그래프 ${\displaystyle G}$의 폐포(영어: closure) ${\displaystyle \operatorname {cl} (G)}$는 다음 성질들을 만족시키는 가장 작은 그래프이다.

• ${\displaystyle V(\operatorname {cl} (G))=V(G)}$
• ${\displaystyle E(\operatorname {cl} (G))\supset E(G)}$
• 임의의 ${\displaystyle u,v\in V(\operatorname {cl} (G))}$에 대하여, ${\displaystyle u}$와 ${\displaystyle v}$가 같은 연결 성분에 속하지만 ${\displaystyle uv\not \in E(\operatorname {cl} (G))}$라면 ${\displaystyle \deg u+\deg v<n}$

이러한 그래프는 유일함을 보일 수 있다.

본디-흐바탈 정리(영어: Bondy–Chvátal theorem)에 따르면, 유한 그래프 ${\displaystyle G}$에 대하여 다음 두 조건이 서로 동치이다.

• ${\displaystyle G}$는 해밀턴 그래프이다.
• ${\displaystyle G}$의 폐포는 해밀턴 그래프이다.

특히, 크기가 3 이상인 완전 그래프는 해밀턴 그래프이므로, 폐포가 완전 그래프인 그래프는 해밀턴 그래프이다. 즉, 다음과 같은 따름정리를 얻을 수 있다. 모든 유한 그래프 ${\displaystyle G}$에 대하여, 만약 ${\displaystyle |V(G)|\geq 3}$라면 다음이 성립한다.

• (디랙의 정리 영어: Dirac’s theorem) 만약 임의의 v에 대해 ${\displaystyle \deg v\geq |V(G)|/2}$라면 ${\displaystyle G}$는 해밀턴 그래프이다.
• (오레의 정리 영어: Ore’s theorem) 만약 모든 인접하지 않은 꼭짓점 ${\displaystyle u,v\in V(G)}$에 대하여 ${\displaystyle \deg u+\deg v\geq |V(G)|}$라면, ${\displaystyle G}$는 해밀턴 그래프이다.

디랙의 정리는 디랙(영어: G. A. Dirac)이 1952년에 증명하였다. 오레의 정리는 외위스테인 오레가 1960년에 증명하였다.

알고리즘

어떤 그래프가 자취 존재 그래프인지 여부를 묻는 결정 문제는 해밀턴 경로 문제라고 하며, NP-완전 문제이다. 마찬가지로, 어떤 그래프가 해밀턴 그래프인지 여부를 묻는 결정 문제는 해밀턴 순환 문제라고 하며, 역시 NP-완전 문제이다. 유향 그래프에 대한 마찬가지 결정 문제 역시 NP-완전 문제이다.

몬테카를로 방법을 사용하여, ${\displaystyle n}$개의 꼭짓점을 갖는 그래프의 해밀턴 순환 문제는 ${\displaystyle O(1.657^{n})}$에 풀 수 있으며, 이분 그래프의 해밀턴 순환 문제는 ${\displaystyle O(1.414^{n})}$에 풀 수 있다.^[1] 퇴각검색 알고리즘을 사용하여, 삼차 그래프의 해밀턴 순환 문제는 ${\displaystyle O(1.251^{n})}$의 시간으로 풀 수 있다.^[2]

예

기사 그래프. 기사의 여행 문제는 기사 그래프의 해밀턴 경로 또는 해밀턴 순환을 찾는 문제이다.

기사 그래프 위의 해밀턴 순환

기사의 여행 문제는 64개의 꼭짓점을 갖는 기사 그래프(영어: knight’s graph)에서 해밀턴 경로와 해밀턴 순환을 찾는 문제이다. 이 그래프는 8×8 체스판에서 나이트가 움직일 수 있는 방향들을 변으로 한다.

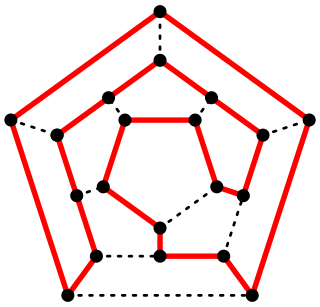
해밀턴 그래프의 예

다음과 같은 그래프들은 해밀턴 그래프이다.

• 크기가 3 이상인 완전 그래프
• 크기가 3 이상인 순환 그래프
• 정다면체의 그래프

다음과 같은 그래프들은 해밀턴 그래프가 아니다.

• 비연결 그래프
• 트리(Tree) 그래프

다음과 같은 그래프는 자취 존재 그래프이지만 해밀턴 그래프가 아니다.

• 2개 이상의 꼭짓점을 갖는 경로 그래프

역사

윌리엄 로언 해밀턴이 1857년에 정십이면체의 그래프 위의 해밀턴 순환을 찾는 문제를 제안하였다. 해밀턴은 이 문제를 아이코시언 게임(영어: icosian game)이라고 불렀다.