빔 스플리터

빔 스플리터(beam splitter)는 빛의 빔을 투과된 빔과 반사된 빔으로 분할하는 광학기구이다. 이는 간섭계와 같은 많은 광학 실험 및 측정 시스템의 중요한 부분이며 광섬유 통신에도 널리 적용된다.

빔 스플리터 큐브의 개략도.
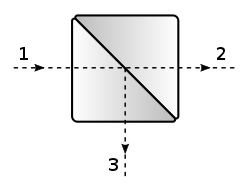
1 - 입사광
2 - 50% 투과광
3 - 50% 반사광
실제로 반사층은 일부 빛을 흡수한다.

설계

가장 일반적인 형태인 큐브인 빔 스플리터는 폴리에스테르, 에폭시 또는 우레탄 기반 접착제를 사용하여 베이스에 함께 접착된 두 개의 삼각형 유리 프리즘으로 만들어진다. (이러한 합성 수지 이전에는 캐나다 발삼과 같은 천연 수지가 사용되었다.) 수지 층의 두께는 (특정 파장에 대해) 하나의 "포트"(즉, 입방체의 면)를 통해 입사되는 빛의 절반이 되도록 조정된다. 반사되고 나머지 절반은 FTIR(Frustrated Total Internal Reflection)로 인해 전송된다. 월라스톤 프리즘과 같은 편광 빔 분할기는 복굴절 재료를 사용하여 빛을 직교 편광 상태의 두 빔으로 분할한다.

알루미늄 코팅 빔 스플리터.

다른 설계는 단방향 거울을 사용하는 것이다. 이것은 부분적으로 투명한 금속 박막 코팅이 되어 있는 광학 기판으로 구성되며, 이 기판은 종종 유리 또는 플라스틱 시트이다. 이 박막 코팅은 물리기상증착 방식으로 알루미늄 증기로부터 증착된 알루미늄일 수 있다. 증착 두께는 45도 각도로 입사하여 코팅이나 기판 재료에 흡수되지 않는 빛의 일부(일반적으로 절반)가 투과되고 나머지는 반사되도록 제어된다. 사진술에 사용되는 매우 얇은 반투과 거울은 종종 펠리클 미러라고 불린다. 반사 코팅에 의한 흡수로 인한 빛 손실을 줄이기 위해, 소위 "스위스 치즈" 빔 스플리터 거울이 사용되었다. 원래 이것들은 원하는 반사 대 투과율을 얻기 위해 구멍이 뚫린 고도로 연마된 금속 시트였다. 나중에는 스퍼터링을 통해 유리에 금속을 증착하여 불연속적인 코팅을 형성하거나, 연속적인 코팅의 작은 부분을 화학적 또는 기계적 작용으로 제거하여 말 그대로 "반투과" 표면을 만들었다.

금속 코팅 대신 다이크로익 광학 코팅이 사용될 수 있다. 특성(박막 간섭)에 따라 반사 대 투과율은 입사광의 파장 함수로 달라진다. 다이크로익 거울은 일부 타원형 반사 스포트라이트에서 불필요한 적외선(열) 복사를 분리하는 데 사용되며, 레이저 제작에서 출력 커플러로 사용된다.

세 번째 빔 스플리터 버전은 다이크로익 미러링 프리즘 어셈블리로, 양색성 광학 코팅을 사용하여 입사광 빔을 여러 스펙트럼적으로 다른 출력 빔으로 나눈다. 이러한 장치는 3개의 픽업 튜브 컬러 텔레비전 카메라와 3스트립 테크니컬러 영화 카메라에 사용되었다. 현재는 현대 3-CCD 카메라에 사용된다. 광학적으로 유사한 시스템은 3개의 LCD 이미지 프로젝터에서 빔 결합기로 역으로 사용되는데, 여기서 세 개의 개별 단색 LCD 디스플레이에서 나오는 빛이 하나의 풀컬러 이미지로 결합되어 투사된다.

PON 네트워크의 빔 스플리터는 종종 단일 모드 광섬유로 만들어지며, 한 쌍의 섬유 사이의 소멸파 결합을 이용하여 빔을 공유한다.^[1] 스플리터는 두 개의 평행한 노출된 섬유를 한 지점에서 융합하여 구성된다.^[2]

하나의 렌즈와 하나의 노출로 스테레오스코피 이미지 쌍을 촬영하기 위한 카메라 부착물로 사용되는 거울 또는 프리즘 배열은 때때로 "빔 스플리터"라고 불리지만, 이는 이미 일치하지 않는 광선을 재지정하는 한 쌍의 잠망경이므로 잘못된 명칭이다. 스테레오스코피 사진 촬영을 위한 일부 매우 드문 부착물에서는 빔 스플리터와 유사한 거울 또는 프리즘 블록이 반대 기능을 수행하여, 두 가지 다른 관점의 피사체 보기를 컬러 필터를 통해 중첩시켜 애너글리프 이미지를 직접 생성하거나, 빠르게 교번하는 셔터를 통해 액정 셔터 안경 비디오를 기록한다.

위상차

유전체 코팅이 있는 빔 스플리터를 통과하는 위상 변화.

빔 스플리터는 마흐-젠더 간섭계에서처럼 광선을 재결합하는 데 사용되기도 한다. 이 경우 두 개의 입사 빔과 잠재적으로 두 개의 출력 빔이 있다. 그러나 두 출력 빔의 진폭은 각 입사 빔에서 계산된 (복소수) 진폭의 합이며, 두 출력 빔 중 하나가 진폭이 0이 될 수 있다. 에너지가 보존되려면(다음 섹션 참조), 적어도 하나의 출력 빔에서 위상 변화가 있어야 한다. 예를 들어 (오른쪽 그림의 빨간색 화살표 참조), 공기 중의 편광된 광파가 유리와 같은 유전체 (물리학) 표면에 부딪히고 광파의 전기장이 표면 평면에 있으면, 반사파는 π의 위상 변화를 가지는 반면, 투과파는 위상 변화를 가지지 않는다. 파란색 화살표는 굴절률이 낮은 매체에서 반사되기 때문에 위상 변화를 얻지 못한다. 이러한 동작은 프레넬 방정식에 의해 결정된다.^[3] 이는 전도성(금속성) 코팅에 의한 부분 반사에는 적용되지 않으며, 이 경우 모든 경로(반사 및 투과)에서 다른 위상 변화가 발생한다. 어떤 경우든 위상 변화의 세부 사항은 빔 스플리터의 유형과 형상에 따라 달라진다.

고전적 무손실 빔 스플리터

두 개의 입사 빔이 있는 빔 스플리터의 경우, 각 입력에 입사하는 전기장 E_a와 E_b를 사용하는 고전적 무손실 빔 스플리터의 두 출력 필드 E_c와 E_d는 다음을 통해 입력과 선형적으로 관련된다.

${\displaystyle \mathbf {E} _{\text{out}}={\begin{bmatrix}E_{c}\\E_{d}\end{bmatrix}}={\begin{bmatrix}r_{ac}&t_{bc}\\t_{ad}&r_{bd}\end{bmatrix}}{\begin{bmatrix}E_{a}\\E_{b}\end{bmatrix}}=\tau \mathbf {E} _{\text{in}},}$

여기서 2×2 요소 ${\displaystyle \tau }$는 빔 스플리터 전달 행렬이고 r과 t는 빔 스플리터를 통과하는 특정 경로를 따라 반사도 및 투과율이며, 해당 경로는 아래첨자에 의해 표시된다. (값은 빛의 편광에 따라 달라진다.)

빔 스플리터가 광선에서 에너지를 제거하지 않으면 총 출력 에너지는 총 입력 에너지와 동일하며 다음을 읽는다.

${\displaystyle |E_{c}|^{2}+|E_{d}|^{2}=|E_{a}|^{2}+|E_{b}|^{2}.}$

위 전달 방정식의 결과를 ${\displaystyle E_{b}=0}$과 함께 삽입하면 다음을 생성한다.

${\displaystyle |r_{ac}|^{2}+|t_{ad}|^{2}=1,}$

마찬가지로 ${\displaystyle E_{a}=0}$일 때

${\displaystyle |r_{bd}|^{2}+|t_{bc}|^{2}=1.}$

${\displaystyle E_{a}}$와 ${\displaystyle E_{b}}$가 모두 0이 아닐 때, 이 두 가지 결과를 사용하면 다음을 얻는다.

${\displaystyle r_{ac}t_{bc}^{\ast }+t_{ad}r_{bd}^{\ast }=0,}$

여기서 "${\displaystyle ^{\ast }}$"는 켤레 복소수를 나타낸다. 이제 ${\displaystyle \tau ^{\dagger }\tau =\mathbf {I} }$ (여기서 ${\displaystyle \mathbf {I} }$는 항등 행렬) 즉, 빔 스플리터 전달 행렬이 유니터리 행렬임을 쉽게 알 수 있다.

각 r과 t는 진폭과 위상 인자를 갖는 복소수로 쓸 수 있다. 예를 들어, ${\displaystyle r_{ac}=|r_{ac}|e^{i\phi _{ac}}}$. 위상 인자는 빔이 해당 표면에서 반사되거나 투과될 때 발생할 수 있는 위상 변화를 설명한다. 그러면 다음을 얻는다.

${\displaystyle |r_{ac}||t_{bc}|e^{i(\phi _{ac}-\phi _{bc})}+|t_{ad}||r_{bd}|e^{i(\phi _{ad}-\phi _{bd})}=0.}$

더 단순화하면 관계는 다음과 같다.

${\displaystyle {\frac {|r_{ac}|}{|t_{ad}|}}=-{\frac {|r_{bd}|}{|t_{bc}|}}e^{i(\phi _{ad}-\phi _{bd}+\phi _{bc}-\phi _{ac})}}$

이는 ${\displaystyle \phi _{ad}-\phi _{bd}+\phi _{bc}-\phi _{ac}=\pi }$이고 지수 항이 -1로 줄어들 때 참이다. 이 새로운 조건을 적용하고 양변을 제곱하면 다음과 같다.

${\displaystyle {\frac {1-|t_{ad}|^{2}}{|t_{ad}|^{2}}}={\frac {1-|t_{bc}|^{2}}{|t_{bc}|^{2}}},}$

여기서 ${\displaystyle |r_{ac}|^{2}=1-|t_{ad}|^{2}}$ 형태의 치환이 이루어졌다. 이는 다음 결과로 이어진다.

${\displaystyle |t_{ad}|=|t_{bc}|\equiv T,}$

그리고 마찬가지로,

${\displaystyle |r_{ac}|=|r_{bd}|\equiv R.}$

따라서 ${\displaystyle R^{2}+T^{2}=1}$이다.

손실 없는 빔 스플리터를 설명하는 제약 조건을 결정한 후, 초기 표현은 다음과 같이 다시 쓸 수 있다.

${\displaystyle {\begin{bmatrix}E_{c}\\E_{d}\end{bmatrix}}={\begin{bmatrix}Re^{i\phi _{ac}}&Te^{i\phi _{bc}}\\Te^{i\phi _{ad}}&Re^{i\phi _{bd}}\end{bmatrix}}{\begin{bmatrix}E_{a}\\E_{b}\end{bmatrix}}.}$^[4]

진폭과 위상에 다른 값을 적용하면 널리 사용되는 많은 다른 형태의 빔 스플리터를 설명할 수 있다.

전달 행렬은 6개의 진폭 및 위상 매개변수를 갖는 것처럼 보이지만, ${\displaystyle R^{2}+T^{2}=1}$ 및 ${\displaystyle \phi _{ad}-\phi _{bd}+\phi _{bc}-\phi _{ac}=\pi }$의 2가지 제약 조건도 갖는다. 제약 조건을 포함하고 4개의 독립 매개변수로 단순화하기 위해 다음과 같이 쓸 수 있다.^[5] ${\displaystyle \phi _{ad}=\phi _{0}+\phi _{T},\phi _{bc}=\phi _{0}-\phi _{T},\phi _{ac}=\phi _{0}+\phi _{R}}$ (그리고 제약 조건으로부터 ${\displaystyle \phi _{bd}=\phi _{0}-\phi _{R}-\pi }$), 그래서

${\displaystyle {\begin{aligned}\phi _{T}&={\tfrac {1}{2}}\left(\phi _{ad}-\phi _{bc}\right)\\\phi _{R}&={\tfrac {1}{2}}\left(\phi _{ac}-\phi _{bd}+\pi \right)\\\phi _{0}&={\tfrac {1}{2}}\left(\phi _{ad}+\phi _{bc}\right)\end{aligned}}}$

여기서 ${\displaystyle 2\phi _{T}}$는 투과된 빔 사이의 위상차이고 ${\displaystyle 2\phi _{R}}$도 마찬가지이며, ${\displaystyle \phi _{0}}$는 전역 위상이다. 마지막으로 ${\displaystyle R^{2}+T^{2}=1}$이라는 다른 제약 조건을 사용하여 ${\displaystyle \theta =\arctan(R/T)}$를 정의한다. 그래서 ${\displaystyle T=\cos \theta ,R=\sin \theta }$이므로

${\displaystyle \tau =e^{i\phi _{0}}{\begin{bmatrix}\sin \theta e^{i\phi _{R}}&\cos \theta e^{-i\phi _{T}}\\\cos \theta e^{i\phi _{T}}&-\sin \theta e^{-i\phi _{R}}\end{bmatrix}}.}$

50:50 빔 스플리터는 ${\displaystyle \theta =\pi /4}$일 때 생성된다. 예를 들어 위의 유전체 빔 스플리터는 다음과 같다.

${\displaystyle \tau ={\frac {1}{\sqrt {2}}}{\begin{bmatrix}1&1\\1&-1\end{bmatrix}},}$

즉, ${\displaystyle \phi _{T}=\phi _{R}=\phi _{0}=0}$인 반면, Loudon의 "대칭" 빔 스플리터^[4]는 다음과 같다.

${\displaystyle \tau ={\frac {1}{\sqrt {2}}}{\begin{bmatrix}1&i\\i&1\end{bmatrix}},}$

즉, ${\displaystyle \phi _{T}=0,\phi _{R}=-\pi /2,\phi _{0}=\pi /2}$.

실험에서의 사용

빔 스플리터는 양자 이론 및 상대론 및 기타 물리학 분야의 사고 실험과 실제 실험 모두에 사용되었다. 여기에는 다음이 포함된다.

• 1851년 물 속에서의 빛의 속도를 측정하기 위한 피조 실험
• 1887년 (가상의) 에테르가 빛의 속도에 미치는 영향을 측정하기 위한 마이컬슨-몰리 실험
• 1935년 데이턴 밀러가 마이컬슨-몰리 실험의 반복에서 긍정적인 결과를 얻었다는 주장을 반박하기 위한 하마 실험
• 1932년 빛의 속도와 측정 장치의 속도 독립성을 테스트하기 위한 케네디-손다이크 실험
• 양자 얽힘의 결과를 시연하고 국소적 숨은 변수 이론을 배제하기 위한 벨 테스트 실험 (약 1972년부터)
• 1978년, 1984년 등에 광자가 파동 또는 입자로 행동하는 것과 그 시기를 테스트하기 위한 휠러의 지연 선택 실험
• 2000년에 제안된 펠릭스 실험은 양자 중첩이 시공간 곡률에 의존한다는 펜로즈 해석을 테스트하기 위한 것
• 상호작용 없는 측정과 관련된 엘리처-바이드만 폭탄 실험을 포함한 다양한 실험에 사용되는 마흐-젠더 간섭계; 그리고 양자 컴퓨팅 분야의 다른 실험들

양자 역학적 설명

양자역학에서 전기장은 2차 양자화와 폭 상태에 의해 설명된 연산자이다. 각 전기장 연산자는 파동 행동과 진폭 연산자를 나타내는 모드로 더 표현될 수 있으며, 이는 일반적으로 무차원 생성 및 소멸 연산자로 표시된다. 이 이론에서 빔 스플리터의 네 포트는 광자 수 상태 ${\displaystyle |n\rangle }$로 표현되고 생성 연산의 작용은 ${\displaystyle {\hat {a}}^{\dagger }|n\rangle ={\sqrt {n+1}}|n+1\rangle }$이다. 다음은 참조.^[5]의 간략화된 버전이다. 빔 스플리터에 의해 생성된 고전적 장 진폭 ${\displaystyle {E}_{a},{E}_{b},{E}_{c}}$ 및 ${\displaystyle {E}_{d}}$ 사이의 관계는 해당 양자 생성 (또는 소멸) 연산자 ${\displaystyle {\hat {a}}_{a}^{\dagger },{\hat {a}}_{b}^{\dagger },{\hat {a}}_{c}^{\dagger }}$ 및 ${\displaystyle {\hat {a}}_{d}^{\dagger }}$의 동일한 관계로 변환되어

${\displaystyle \left({\begin{matrix}{\hat {a}}_{c}^{\dagger }\\{\hat {a}}_{d}^{\dagger }\end{matrix}}\right)=\tau \left({\begin{matrix}{\hat {a}}_{a}^{\dagger }\\{\hat {a}}_{b}^{\dagger }\end{matrix}}\right)}$

여기서 전달 행렬은 위에 있는 고전적 무손실 빔 스플리터 섹션에 주어진다.

${\displaystyle \tau =\left({\begin{matrix}r_{ac}&t_{bc}\\t_{ad}&r_{bd}\end{matrix}}\right)=e^{i\phi _{0}}\left({\begin{matrix}\sin \theta e^{i\phi _{R}}&\cos \theta e^{-i\phi _{T}}\\\cos \theta e^{i\phi _{T}}&-\sin \theta e^{-i\phi _{R}}\end{matrix}}\right).}$

${\displaystyle \tau }$가 유니터리이므로, ${\displaystyle \tau ^{-1}=\tau ^{\dagger }}$, 즉

${\displaystyle \left({\begin{matrix}{\hat {a}}_{a}^{\dagger }\\{\hat {a}}_{b}^{\dagger }\end{matrix}}\right)=\left({\begin{matrix}r_{ac}^{\ast }&t_{ad}^{\ast }\\t_{bc}^{\ast }&r_{bd}^{\ast }\end{matrix}}\right)\left({\begin{matrix}{\hat {a}}_{c}^{\dagger }\\{\hat {a}}_{d}^{\dagger }\end{matrix}}\right).}$

이는 우리가 진공 상태 ${\displaystyle |00\rangle _{ab}}$에서 시작하여 포트 a에 광자를 추가하여

${\displaystyle |\psi _{\text{in}}\rangle ={\hat {a}}_{a}^{\dagger }|00\rangle _{ab}=|10\rangle _{ab},}$

를 생성하면, 빔 스플리터가 다음과 같은 출력에서 중첩을 생성한다는 것과 동등하다.

${\displaystyle |\psi _{\text{out}}\rangle =\left(r_{ac}^{\ast }{\hat {a}}_{c}^{\dagger }+t_{ad}^{\ast }{\hat {a}}_{d}^{\dagger }\right)|00\rangle _{cd}=r_{ac}^{\ast }|10\rangle _{cd}+t_{ad}^{\ast }|01\rangle _{cd}.}$

따라서 광자가 포트 c와 d로 나갈 확률은 예상대로 ${\displaystyle |r_{ac}|^{2}}$와 ${\displaystyle |t_{ad}|^{2}}$이다.

마찬가지로, 모든 입력 상태 ${\displaystyle |nm\rangle _{ab}}$에 대해

${\displaystyle |\psi _{\text{in}}\rangle =|nm\rangle _{ab}={\frac {1}{\sqrt {n!}}}\left({\hat {a}}_{a}^{\dagger }\right)^{n}{\frac {1}{\sqrt {m!}}}\left({\hat {a}}_{b}^{\dagger }\right)^{m}|00\rangle _{ab}}$

출력은 다음과 같다.

${\displaystyle |\psi _{\text{out}}\rangle ={\frac {1}{\sqrt {n!}}}\left(r_{ac}^{\ast }{\hat {a}}_{c}^{\dagger }+t_{ad}^{\ast }{\hat {a}}_{d}^{\dagger }\right)^{n}{\frac {1}{\sqrt {m!}}}\left(t_{bc}^{\ast }{\hat {a}}_{c}^{\dagger }+r_{bd}^{\ast }{\hat {a}}_{d}^{\dagger }\right)^{m}|00\rangle _{cd}.}$

다항 이항 정리를 사용하면 다음과 같이 쓸 수 있다.

${\displaystyle {\begin{aligned}|\psi _{\text{out}}\rangle &={\frac {1}{\sqrt {n!m!}}}\sum _{j=0}^{n}\sum _{k=0}^{m}{\binom {n}{j}}\left(r_{ac}^{\ast }{\hat {a}}_{c}^{\dagger }\right)^{j}\left(t_{ad}^{\ast }{\hat {a}}_{d}^{\dagger }\right)^{(n-j)}{\binom {m}{k}}\left(t_{bc}^{\ast }{\hat {a}}_{c}^{\dagger }\right)^{k}\left(r_{bd}^{\ast }{\hat {a}}_{d}^{\dagger }\right)^{(m-k)}|00\rangle _{cd}\\&={\frac {1}{\sqrt {n!m!}}}\sum _{N=0}^{n+m}\sum _{j=0}^{N}{\binom {n}{j}}r_{ac}^{\ast j}t_{ad}^{\ast (n-j)}{\binom {m}{N-j}}t_{bc}^{\ast (N-j)}r_{bd}^{\ast (m-N+j)}\left({\hat {a}}_{c}^{\dagger }\right)^{N}\left({\hat {a}}_{d}^{\dagger }\right)^{M}|00\rangle _{cd},\\&={\frac {1}{\sqrt {n!m!}}}\sum _{N=0}^{n+m}\sum _{j=0}^{N}{\binom {n}{j}}{\binom {m}{N-j}}r_{ac}^{\ast j}t_{ad}^{\ast (n-j)}t_{bc}^{\ast (N-j)}r_{bd}^{\ast (m-N+j)}{\sqrt {N!M!}}\quad |N,M\rangle _{cd},\end{aligned}}}$

여기서 ${\displaystyle M=n+m-N}$이고 ${\displaystyle {\tbinom {n}{j}}}$는 이항 계수이며, ${\displaystyle j\notin \{0,n\}}$ 등일 경우 계수는 0으로 이해되어야 한다.

마지막 방정식의 투과/반사 계수 인자는 유니터리성을 보장하는 축소된 매개변수로 작성될 수 있다.

${\displaystyle r_{ac}^{\ast j}t_{ad}^{\ast (n-j)}t_{bc}^{\ast (N-j)}r_{bd}^{\ast (m-N+j)}=(-1)^{j}\tan ^{2j}\theta (-\tan \theta )^{m-N}\cos ^{n+m}\theta \exp -i\left[(n+m)(\phi _{0}+\phi _{T})-m(\phi _{R}+\phi _{T})+N(\phi _{R}-\phi _{T})\right].}$

여기서 빔 스플리터가 50:50이면 ${\displaystyle \tan \theta =1}$이고 j에 의존하는 유일한 인자는 ${\displaystyle (-1)^{j}}$ 항임을 알 수 있다. 이 인자는 흥미로운 간섭 소멸을 일으킨다. 예를 들어, ${\displaystyle n=m}$이고 빔 스플리터가 50:50이면 다음과 같다.

${\displaystyle {\begin{aligned}\left({\hat {a}}_{a}^{\dagger }\right)^{n}\left({\hat {a}}_{b}^{\dagger }\right)^{m}&\to \left[{\hat {a}}_{a}^{\dagger }{\hat {a}}_{b}^{\dagger }\right]^{n}\\&=\left[\left(r_{ac}^{\ast }{\hat {a}}_{c}^{\dagger }+t_{ad}^{\ast }{\hat {a}}_{d}^{\dagger }\right)\left(t_{bc}^{\ast }{\hat {a}}_{c}^{\dagger }+r_{bd}^{\ast }{\hat {a}}_{d}^{\dagger }\right)\right]^{n}\\&=\left[{\frac {e^{-i\phi _{0}}}{\sqrt {2}}}\right]^{2n}\left[\left(e^{-i\phi _{R}}{\hat {a}}_{c}^{\dagger }+e^{-i\phi _{T}}{\hat {a}}_{d}^{\dagger }\right)\left(e^{i\phi _{T}}{\hat {a}}_{c}^{\dagger }-e^{i\phi _{R}}{\hat {a}}_{d}^{\dagger }\right)\right]^{n}\\&={\frac {e^{-2in\phi _{0}}}{2^{n}}}\left[e^{i(\phi _{T}-\phi _{R})}\left({\hat {a}}_{c}^{\dagger }\right)^{2}+e^{-i(\phi _{T}-\phi _{R})}\left({\hat {a}}_{d}^{\dagger }\right)^{2}\right]^{n}\end{aligned}}}$

여기서 ${\displaystyle {\hat {a}}_{c}^{\dagger }{\hat {a}}_{d}^{\dagger }}$ 항은 소멸되었다. 따라서 출력 상태는 항상 각 팔에 짝수 개의 광자를 갖는다. 이것의 유명한 예는 홍-오우-만델 효과인데, 여기서 입력은 ${\displaystyle n=m=1}$이고, 출력은 항상 ${\displaystyle |20\rangle _{cd}}$ 또는 ${\displaystyle |02\rangle _{cd}}$이다. 즉, 각 모드에 광자가 있는 출력(우연 사건)의 확률은 0이다. 이는 위상의 세부 사항과 관계없이 모든 유형의 50:50 빔 스플리터에 대해 참이며, 광자는 구별할 수 없기만 하면 된다. 이는 고전적 결과와 대조되는데, 고전적 결과에서는 50:50 빔 스플리터의 동일한 입력에 대해 양쪽 팔에서 동일한 출력이 특정 빔 스플리터 위상(예: 대칭 빔 스플리터 ${\displaystyle \phi _{0}=\phi _{T}=0,\phi _{R}=\pi /2}$)에 대해 나타나며, 다른 위상에서 출력은 한쪽 팔로 이동한다(예: 유전체 빔 스플리터 ${\displaystyle \phi _{0}=\phi _{T}=\phi _{R}=0}$) 출력은 항상 같은 팔에 있으며, 여기처럼 양쪽 팔에서 무작위가 아니다. 대응원리로부터 우리는 양자 결과가 큰 n의 한계에서 고전적 결과로 수렴할 것으로 예상할 수 있지만, 입력에 많은 수의 구별할 수 없는 광자의 출현은 고전적 장 패턴에 해당하지 않는 비고전적 상태이며, 대신 다른 ${\displaystyle |n,m\rangle }$의 통계적 혼합을 생성하며 이는 포아송 광으로 알려져 있다.

엄격한 유도는 Fearn–Loudon 1987년 논문^[6]에 주어져 있으며, 참조^[5]에서 밀도 행렬과의 통계적 혼합을 포함하도록 확장되었다.

비대칭 빔 스플리터

일반적으로 투과 및 반사 계수가 같지 않은 비대칭 빔 스플리터의 경우 다음과 같은 각도 ${\displaystyle \theta }$를 정의할 수 있다.

${\displaystyle {\begin{cases}|R|=\sin(\theta )\\|T|=\cos(\theta )\end{cases}}}$

여기서 ${\displaystyle R}$과 ${\displaystyle T}$는 반사 및 투과 계수이다. 그러면 빔 스플리터와 관련된 유니터리 연산은 다음과 같다.

${\displaystyle {\hat {U}}=e^{i\theta \left({\hat {a}}_{a}^{\dagger }{\hat {a}}_{b}+{\hat {a}}_{a}{\hat {a}}_{b}^{\dagger }\right)}.}$

양자 컴퓨팅을 위한 응용

2000년 크닐, 라플람, 밀번(KLM 프로토콜)은 빔 스플리터, 위상 변환기, 광검출기 및 단일 광자 소스만으로 범용 양자 컴퓨터를 만들 수 있음을 입증했다. 이 프로토콜에서 큐비트를 형성하는 상태는 두 모드의 단일 광자 상태, 즉 두 모드의 점유 수 표현(폭 상태)에서 |01⟩ 및 |10⟩ 상태이다. 이러한 자원을 사용하여 모든 단일 큐비트 게이트 및 2-큐비트 확률 게이트를 구현할 수 있다. 빔 스플리터는 이 구성에서 필수적인 구성 요소인데, 이는 양자 얽힘을 폭 상태 사이에 생성하는 유일한 요소이기 때문이다.

연속 변수 양자 정보 처리를 위한 유사한 설정이 존재한다. 실제로, 두 모드 스퀴즈드 진공 상태가 사전 자원으로만 사용 가능하다면 빔 스플리터, 위상 변환기 및 광검출기를 사용하여 빛의 양자 상태에 대한 임의의 가우시안 (보골류보프) 변환을 시뮬레이션할 수 있다 (이 설정은 따라서 KLM 프로토콜의 가우시안 대응물과 특정 유사점을 공유한다).^[7] 이 시뮬레이션 절차의 구성 요소는 빔 스플리터가 부분 시간 역전 대칭 하에서 스퀴즈 변환과 동등하다는 사실이다.

회절 빔 스플리터

 이 부분의 본문은 회절 빔 스플리터입니다.

반사 빔 스플리터

파이로전기 센서(4개 광학 채널)에서 반사 빔 스플리터의 원리 도면

반사 빔 스플리터는 입사 복사의 일부를 다른 방향으로 반사시킨다. 이 부분 빔들은 정확히 동일한 강도를 보인다. 일반적으로 반사 빔 스플리터는 금속으로 만들어지며 광대역 스펙트럼 특성을 갖는다.

콤팩트한 설계 덕분에 이러한 유형의 빔 스플리터는 적외선 검출기에 특히 쉽게 설치할 수 있다.^[8] 이 응용 분야에서 복사는 검출기의 조리개 개구를 통해 유입되어 내부 고반사 미세 구조에 의해 동일한 강도이지만 다른 방향의 여러 빔으로 분할된다. 각 빔은 상류의 광학 필터가 있는 센서 요소에 도달한다. 특히 NDIR 가스 분석에서 이 설계는 최소 빔 단면을 가진 단일 빔으로 측정을 가능하게 하여 측정의 간섭 면역성을 크게 높인다.

같이 보기

• 전력 분배기 및 방향성 결합기