Комплемент

Во теоријата на множества и други гранки на математиката, дефинирани се два вида на комплементи: релативен комплемент и апсолутен комплемент.

Ако A е област која е обоена во црвено на оваа слика...

...тогаш комплементот на A е се друго.

Релативен комплемент

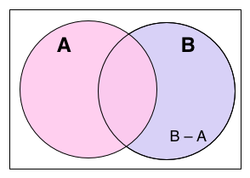
Ако A и B се множества, тогаш релативниот комплемент на A во B, познат и како разлика на множества меѓу B и A, е множеството чии елементи припаѓаат на B, но не припаѓаат на A.

B minus A

Релативниот комплемент
на A во B

Релативниот комплемент на A во B обично се пишува B − A (исто така и B \ A).

Формално:

${\displaystyle B-A=\{x\in B\,|\,x\not \in A\}.}$

Примери:

• {1,2,3} − {2,3,4}   =   {1}
• {2,3,4} − {1,2,3}   =   {4}
• Ако ${\displaystyle \mathbb {R} }$ е е множеството на реални броеви и ${\displaystyle \mathbb {Q} }$ е множеството на рационални броеви, тогаш ${\displaystyle \mathbb {R} -\mathbb {Q} }$ е множеството на ирационални броеви.

Следните изрази ги покажуваат некои важни особини на релативните комплементи во однос на операциите унија и пресек од теорија на множества.

PROPOSITION 1: Ако A, B, и C се множества, тогаш важат следните идентитети:

• C − (A ∩B)  =  (C − A) ∪(C − B)
• C − (A ∪B)  =  (C − A) ∩(C − B)
• C − (B − A)  =  (A ∩C) ∪(C − B)
• (B − A) ∩C  =  (B ∩C) − A  =  B ∩(C − A)
• (B − A) ∪C  =  (B ∪C) − (A − C)
• A − A  =  Ø
• Ø − A  =  Ø
• A − Ø  =  A

Апсолутен комплемент

A complement

Комплементот на A во U

Ако е дефинирано универзално множество U, тогаш релативниот комплемент на A во U се нарекува апсолутен комплемент (или едноставно комплемент) на A, и се означува со A^C, што значи:

A^C  = U − A

На пример, ако универзалното множество е множеството на природни броеви, тогаш комплементот на множеството непарни броеви е множеството парни броеви.

Следниот израз ги покажува некои важни особини на апсолутните комплементи во однос на операциите унија и пресек од теорија на множества.

Ако A и B се подможества на универзално множество U, тогаш важат следните идентитети:

Де Морганови закони:

• (A ∪ B)^C  = A^C ∩ B^C
• (A ∩ B)^C  = A^C ∪ B^C

Закони за комплемент:

• A ∪ A^C  =  U
• A ∩ A^C  =  Ø
• Ø^C  =  U
• U^C  =  Ø
• Ако A⊆B, тогаш B^C⊆A^C

Инволуција или закон за двоен комплемент:

• A^CC  =  A.

Релации помеѓу релативен и апсолутен комплемент:

• A − B = A ∩ B^C
• (A − B)^C = A^C ∪ B

Првите два горенаведени закони за комплемент покажуваат дека ако A е непразно подмножество на U, тогаш {A, A^C} е партиција на U.