അവകലജം

വാസ്തവികസംഖ്യകൾ ( real numbers) മൂല്യമായി എടുക്കുന്ന ചരത്തിന്റെ ( variable) ഒരു ഫലനം ( function) ഉണ്ടെന്നു കരുതുക. ഈ ഫലനത്തിലേയ്ക്ക് ഓരോ സംഖ്യ ഇൻപുട്ട് കൊടുക്കുമ്പോളും മറ്റൊരു സംഖ്യ ഔട്ട്പുട്ട് ആയി തിരിച്ചുകിട്ടുന്നു. വേറൊരു തരത്തിൽ പറഞ്ഞാൽ ഇൻപുട്ട് മാറും തോറും ഫലനത്തിന്റെ ഔട്ട്പുട്ടും മാറുന്നു. ഇൻപുട്ടിൽ ഉള്ള ഓരോ ചെറിയ മാറ്റത്തിനനുസരിച്ച് ഒരു ഫലനത്തിന്റെ ഔട്ട്പുട്ടിൽ എന്തുമാത്രം മാറ്റമുണ്ടാകുന്നു എന്ന വിലയാണ് ആ ഫലനത്തിന്റെ അവകലജം.( derivative).^[1]

ഒരു ഫലനത്തിന്റെ ആരേഖം, കറുത്ത നിറത്തിൽ ചിത്രീകരിച്ചിരിയ്ക്കുന്നു. അതിന്റെ ഒരു സ്പർശകം ( tangent) ചുവന്ന നിറത്തിലും. ആ സ്പർശരേഖയുടെ ആനതിയും ( slope) ആ ഫലനത്തിന്റെ ആ അടയാളപ്പെടുത്തിയിട്ടുള്ള ബിന്ദുവിലെ അവകലജത്തിന്റ വിലയും തുല്യമായിരിയ്ക്കും.

ഉദാഹരണത്തിന് ചലിച്ചുകൊണ്ടിരിയ്ക്കുന്ന ഒരു വസ്തുവിന്റെ ഒരു വസ്തുവിന്റെ സ്ഥാനം (position) സമയത്തിനനുസരിച്ച് മാറിക്കൊണ്ടിരിയ്ക്കുന്നു. ഇവിടെ സമയത്തിന്റെ ഒരു ഫലനമാണ് സ്ഥാനം എന്ന് പറയാം. ഇനി സമയത്തിലുള്ള ഓരോ ചെറിയ വ്യത്യാസത്തിനും സ്ഥാനത്തിൽ എന്തു വ്യത്യാസം വരുന്നുണ്ടെന്നു നമുക്കു കണക്കാക്കാം. (എങ്ങനെ എന്നത് പിന്നീട് കാണാം). ഈ വ്യത്യാസത്തെയാണ് വസ്തുവിന്റെ പ്രവേഗം ( velocity) എന്ന് വിളിയ്ക്കുന്നത്.^[2] (പൊതുവെ സംസാരഭാഷയിലെ വേഗത / സ്പീഡ് എന്നതിന്റെ ഭൗതികശാസ്ത്രത്തിലെ കുറച്ചുകൂടി കൃത്യതയാർന്ന ഒരു നിർവചനമാണ് പ്രവേഗം. വേഗതയ്ക്ക് ദിശയില്ല, പ്രവേഗത്തിന് ഒരു നിശ്ചിത ദിശയുണ്ട്). ഇവിടെ ഒരു കാര്യം ശ്രദ്ധിക്കാനുള്ളത് പൊതുവേ പറയുമ്പോൾ പ്രവേഗം എപ്പോഴും സ്ഥിരമായിരിയ്ക്കണം എന്നില്ല. അതായത് പ്രവേഗവും സമയത്തിന്റെ ഒരു ഫലനമായി കണക്കാക്കാം. അതായത് ഒരു ഫലനത്തിന്റെ അവകലജം മറ്റൊരു ഫലനം ആയിരിയ്ക്കും.^[3]

ഒരു ചരത്തെ അടിസ്ഥാനമായുള്ള ഒരു ഫലനത്തിന്റെ ഗ്രാഫിലെ ഒരു ബിന്ദുവിലൂടെ ആ ഫലനത്തിന് ഒരു സ്പർശരേഖ ( tangent) വരച്ചാൽ അതിന്റെ ആനതിയും ( slope) ആ ഫലനത്തിന്റെ അതേ ബിന്ദുവിലെ അവകലജത്തിന്റ വിലയും തുല്യമായിരിയ്ക്കും.^[4] ഒരു ഫലനത്തിലെ ഓരോ ബിന്ദുവിലും വെച്ച് ഫലനത്തിന്റെ ഔട്ട്പുട്ട് വില എത്രമാത്രം മാറുന്നു എന്നുള്ളതിന്റെ വിലയാണ് അവകലജം. അതിനാൽ അവകലജത്തെ ഒരു ഫലനത്തിന്റെ ഒരോ ബിന്ദുവിലെയും തൽസ്ഥലമാറ്റത്തിന്റെ നിരക്ക് എന്നും വിശേഷിപ്പിയ്ക്കാറുണ്ട്.

അവകലജം കണ്ടുപിടിയ്ക്കുന്ന പ്രക്രിയയാണ് അവകലനം (differentiation).

ഇനി ഫലനത്തിന്റെ മേൽപ്പറഞ്ഞ നിർവചനത്തെ വിപുലീകരിയ്ക്കാം. ഫലനം ഒരു ചരത്തിന്റെ തന്നെ ആകണമെന്നില്ല. വാസ്തവികസംഖ്യകൾ വിലകളായി എടുക്കുന്ന പല ചരങ്ങളുടെയും ആകാം. ഇത്തരം ഫലനങ്ങളുടെ അവകലജം കണക്കാക്കുമ്പോൾ ഓരോ ചരത്തെയായി പ്രത്യേകം എടുത്തു അവകലനം ചെയ്യേണ്ടിവരും. ഓരോ ബിന്ദുവിലും ഈ ഭാഗിക അവകലനം ( partial differentiation) ചെയ്തുകിട്ടുന്ന വിലകൾ ഒരു സംഖ്യ ആകില്ല, പകരം ഒരു സദിശം അഥവാ വെക്റ്റർ ആകും. ഇതിനെ ഗ്രേഡിയന്റ് വെക്റ്റർ എന്ന് വിളിയ്ക്കുന്നു.^[5]

അവകലനം

അവകലജം കണ്ടുപിടിയ്ക്കുന്ന പ്രക്രിയയാണ് അവകലനം (differentiation). y = f(x) എന്ന x 'ന്റെ ഫലനത്തിൽ x 'നു അനുസരിച്ച y മാറുന്ന നിരക്കാണ് f ന്റെ അവകലജം. xഉം yഉം വാസ്തവികസംഖ്യകൾ ആണെങ്കിൽ അവയെ ഒരു ആരേഖത്തിൽ(graph) വരച്ചാൽ കിട്ടുന്ന നിഷ്കോണവക്രത്തിന്റെ ഓരോ ബിന്ദുവിലുമുള്ള ആനതിയാണ് (slope) ആ ബിന്ദുവിലെ f അവകലജവില.^[1] f ഒരു രേഖീയഫലനം (linear function) ആണെങ്കിൽ f'ന്റെ അവകലജം എല്ലാ ബിന്ദുവിലും സ്ഥിരമായിരിയ്ക്കും. പൊതുവേ f 'ന്റെ അവകലജം വീണ്ടും ഒരു ഫലനം ആയിരിയ്ക്കും.^[3]

നോറ്റെഷൻ

അടയാളയപ്പെടുത്തിയിരിയ്ക്കുന്ന ബിന്ദുവിൽ സ്റ്റെപ് ഫലനത്തിന് ഒരു അവകലജം കണ്ടുപിടിയ്ക്കാൻ സാധ്യമല്ല. അതിനാൽ ആ ബിന്ദുവിൽ അത് ഡിഫറെൻഷ്യബിൾ അല്ല.

രണ്ടുതരം ചിഹ്നങ്ങൾ വഴി അവകലജത്തെ രേഖപ്പെടുത്താറുണ്ട്. ലെയ്‌ബ്‌നിസ് നോറ്റെഷൻ : x'ലെ അനന്തസൂക്ഷ്മമായ ( Infinitesimal) മാറ്റം dx ആണെന്ന് കരുതിയാൽ x'നെ അപേക്ഷിച്ച് y 'ടെ (അല്ലെങ്കിൽ f 'ന്റെ) അവകലജത്തെ ഇങ്ങനെ രേഖപ്പെടുത്തുന്നു.^[6]

${\displaystyle {\frac {dy}{dx}}}$

ഇവിടെ അവകലജം രണ്ടു അതിസൂക്ഷ്മവിലകളുടെ അംശബന്ധം ആണെന്ന് സൂചന (യഥാർത്ഥത്തിൽ ഇതൊരു അംശബന്ധം അല്ല എന്നോർക്കുക. ഇതൊരു നോറ്റെഷൻ മാത്രമാണ്. മുകളിലും താഴെയുമുള്ള d വെട്ടിക്കളയാൻ പാടില്ല.)

ലഗ്രാഞ്ഞെ നോറ്റെഷൻ : x'നെ അപേക്ഷിച്ച് y 'ടെ (അല്ലെങ്കിൽ f 'ന്റെ) അവകലജത്തെ f'(x) എന്ന് രേഖപ്പെടുത്തുന്നു.^[7]

നിർവചനം

കേവലവിലകളുടെ ഫലനം അനുസ്യൂതം ആണ്. എന്നാൽ x = 0 എന്ന ബിന്ദുവിൽ ഇതിന്റെ ആനതി കണ്ടുപിടിയ്ക്കാൻ ശ്രമിച്ചാൽ നമുക്ക് രണ്ടു വിലകൾ കിട്ടും. ഇടത്തുനിന്നും ആനതിയുടെ ലിമിറ്റ് കണ്ടുപിടിയ്ക്കാൻ ശ്രമിച്ചാൽ കിട്ടുന്ന അതേ വിലയല്ല വലത്തുനിന്നും കണ്ടുപിടിയ്ക്കാൻ ശ്രമിച്ചാൽ കിട്ടുന്നത്.

y = f(x) എന്ന x 'ന്റെ ഫലനത്തിന്റെ അവകലജം ${\displaystyle {\frac {dy}{dx}}}$ താഴെക്കൊടുത്തിട്ടുള്ളതാണ്.^[8]

${\displaystyle {\frac {dy}{dx}}=\lim _{\Delta x\to 0}{\frac {f(x+\Delta x)-f(x)}{\Delta x}}}$

സാധാരണഭാഷയിൽ ഈ സൂത്രവാക്യത്തെ ഇങ്ങനെ വിശദീകരിയ്ക്കാം. ഇൻപുട്ട് വിലകളുടെ ചെറിയ മാറ്റത്തിനനുസരിച്ച് ഒരു ഫലനത്തിന്റെ ഔട്ട്പുട്ട് വിലയിൽ ഉണ്ടാകുന്ന മാറ്റത്തിന്റെ നിരക്കാണ് അവകലജം എന്ന് മുകളിൽ പറഞ്ഞല്ലോ.

ഇൻപുട്ട് വിലകൾ ആണ് x എന്നതുകൊണ്ട് സൂചിപ്പിയ്ക്കുന്നത്.

ഇൻപുട്ട് വിലകളുടെ ചെറിയ മാറ്റം ആണ് ${\displaystyle \Delta x}$ (x ന്റെ ചെറിയ മാറ്റം).

x ലും അല്പം മാറിയ ${\displaystyle x+\Delta x}$ ലും ഉള്ള ഫലനത്തിന്റ ഔട്ട്പുട്ട് വിലകൾ ആണ് യഥാക്രമം f(x) ഉം f(${\displaystyle x+\Delta x}$) ഉം.

അവയുടെ വ്യത്യാസം f(${\displaystyle x+\Delta x}$) - f(x).

അതിന്റെ നിരക്ക് ${\displaystyle {\frac {f(x+\Delta x)-f(x)}{\Delta x}}}$.

ഇനി ഇതിന്റെ ലിമിറ്റ് എടുക്കുക. അതായത് അതിസൂക്ഷ്മമായ ${\displaystyle \Delta x}$ എത്ര കുറയ്ക്കാമോ അത്രയ്ക്കും കുറയ്ക്കുക. ഈ പറയുന്ന പ്രസ്താവനയുടെ ഗണിതരൂപമാണ് ${\displaystyle \lim _{\Delta x\to 0}}$ എന്നത്.

ഈ പ്രസ്താവന മുകളിൽ കൊടുത്തിരിയ്ക്കുന്ന നിരക്കിന്റെ സൂത്രവാക്യത്തിൽ പ്രയോഗിയ്ക്കുക. അപ്പോൾ അവകലജത്തിന്റെ സൂത്രവാക്യം ആയി.

ഉദാഹരണം:

f(x) = x² എന്ന ഫലനം എടുക്കുക. ഇതിന്റെ a എന്ന വിലയ്ക്കുള്ള അവകലജം മുകളിൽ പറഞ്ഞ ലിമിറ്റ് ഉപയോഗിച്ചുള്ള സൂത്രവാക്യം ഉപയോഗിച്ച് കണ്ടെത്താൻ ശ്രമിയ്ക്കാം.

${\displaystyle {\begin{aligned}f'(a)&=\lim _{h\to 0}{\frac {f(a+h)-f(a)}{h}}=\lim _{h\to 0}{\frac {(a+h)^{2}-a^{2}}{h}}\\[0.3em]&=\lim _{h\to 0}{\frac {a^{2}+2ah+h^{2}-a^{2}}{h}}=\lim _{h\to 0}{\frac {2ah+h^{2}}{h}}\\[0.3em]&=\lim _{h\to 0}{(2a+h)}=2a\end{aligned}}}$

അനുസ്യൂതിയും അവകലനതയും (ഡിഫറെൻഷ്യബിലിറ്റി)

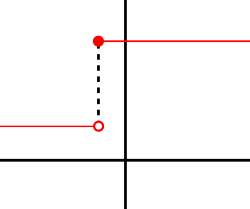
x ന്റെ എല്ലാ വിലകൾക്കും ഈ ലിമിറ്റ് വില കണ്ടുപിടിയ്ക്കാൻ പറ്റണം എന്നില്ല. അങ്ങനെ പറ്റുമെങ്കിൽ f എന്ന ഫലനത്തിന് അവകലനത (ഡിഫറെൻഷ്യബിൾ ( differentiable)) പറയുന്നു.^[9] അവകലനത ഇല്ലാത്ത ഒരു ഫലനത്തിന്റെ ഉദാഹരണമാണ് സ്റ്റെപ് ഫലനം. ഉദാഹരണത്തിന് a എന്ന ബിന്ദുവിൽ വെച്ച് പെട്ടെന്ന് വില മാറുന്ന (ഇതാണ് സ്റ്റെപ്) സ്റ്റെപ് ഫലനത്തെ വലതുവശത്ത് വരച്ചിരിയ്ക്കുന്ന ആരേഖത്തിൽ കാണിച്ചിരിയ്ക്കുന്ന. a എന്ന ബിന്ദുവിൽ ഫലനം അനുസ്യൂതം (continuous) അല്ല. തൽഫലമായി a എന്ന ബിന്ദുവിലൂടെ ഇതിന്റെ ആരേഖത്തിന് ഒരു ആനതി വരയ്ക്കാൻ സാധ്യമല്ല. ഒരു ഫലനത്തിന് അവകലനത ഉണ്ടാകണമെങ്കിൽ അത് അനുസ്യൂതം ആയിരിയ്ക്കണം. എന്നാൽ അനുസ്യൂതം ആയിരുന്നതുകൊണ്ടു മാത്രം ഒരു ഫലനത്തിന് അവകലനത ഉണ്ടാകണമെന്നില്ല.^[9] കേവലവിലകളുടെ ഫലനം (y = |x|) ശ്രദ്ധിയ്ക്കുക. ഇത് അനുസ്യൂതം ആണ്. എന്നാൽ 0 എന്ന x വിലയിൽ വച്ച് ഫലനത്തിന് ഒരു 'ഒടിവ്' സംഭവിയ്ക്കുന്നത് കാണുക. ഈ ബിന്ദുവിൽ ഇതിന്റെ ആനതി കണ്ടുപിടിയ്ക്കാൻ ശ്രമിച്ചാൽ നമുക്ക് രണ്ടു വിലകൾ കിട്ടും. ഇടത്തുനിന്നും ആനതിയുടെ ലിമിറ്റ് (ആനതിയുടെ ലിമിറ്റ് ആണല്ലോ അവകലജം) കണ്ടുപിടിയ്ക്കാൻ ശ്രമിച്ചാൽ കിട്ടുന്ന അതേ വിലയല്ല വലത്തുനിന്നും കണ്ടുപിടിയ്ക്കാൻ ശ്രമിച്ചാൽ കിട്ടുന്നത്. അതായത് ഈ ബിന്ദുവിൽ ഈ ഫലനത്തിന് അവകലനത ഇല്ല എന്നർത്ഥം.

ചില സാധാരണ ഫലങ്ങളുടെ അവകലജങ്ങൾ

• ഘാത നിയമം ([[Derivatives of powers]]):

${\displaystyle f(x)=x^{r},}$

r ഒരു വാസ്തവികസംഖ്യ യാണെങ്കിൽ,

${\displaystyle f'(x)=rx^{r-1},}$

ഉദാഹരണത്തിന്, ${\displaystyle f(x)=x^{1/4}}$ ആണെങ്കിൽ,

${\displaystyle f'(x)=(1/4)x^{-3/4},}$

• ഘാതഫലനവും (Exponential) ലോഗരിതഫലനവും ( logarithmic function):

${\displaystyle {\frac {d}{dx}}e^{x}=e^{x}.}$

${\displaystyle {\frac {d}{dx}}a^{x}=a^{x}\ln(a).}$

${\displaystyle {\frac {d}{dx}}\ln(x)={\frac {1}{x}},\qquad x>0.}$

${\displaystyle {\frac {d}{dx}}\log _{a}(x)={\frac {1}{x\ln(a)}}.}$

• ത്രികോണമിതി ഫലനങ്ങൾ ( Trigonometric function):

${\displaystyle {\frac {d}{dx}}\sin(x)=\cos(x).}$

${\displaystyle {\frac {d}{dx}}\cos(x)=-\sin(x).}$

${\displaystyle {\frac {d}{dx}}\tan(x)=\sec ^{2}(x)={\frac {1}{\cos ^{2}(x)}}=1+\tan ^{2}(x).}$

• ത്രികോണമിതി എതിർ ഫലനങ്ങൾ ( Inverse trigonometric function):

${\displaystyle {\frac {d}{dx}}\arcsin(x)={\frac {1}{\sqrt {1-x^{2}}}},-1<x<1.}$

${\displaystyle {\frac {d}{dx}}\arccos(x)=-{\frac {1}{\sqrt {1-x^{2}}}},-1<x<1.}$

${\displaystyle {\frac {d}{dx}}\arctan(x)={\frac {1}{1+x^{2}}}}$

പല ഫലനങ്ങൾ ചേർന്നുള്ള സൂത്രവാക്യങ്ങളുടെ അവകലജം

പല സന്ദർഭങ്ങളിലും നമുക്ക് സങ്കീർണമായ ഫലനങ്ങളുടെ അവകലജം കണ്ടുപിടിയ്ക്കേണ്ടി വരും. അവയെ ഒന്നിലേറെ ഫലനങ്ങളുടെ സംയോഗം ആക്കി എഴുതിയാൽ താഴെകൊടുത്തിരിയ്ക്കുന്ന നിയമങ്ങൾ വഴി അവയുടെ അവകലജം കണ്ടുപിടിയ്ക്കാൻ.

• '''സ്ഥിരവിലനിയമം''': f(x) എന്നത് സ്ഥിരവില (constant) ആണെങ്കിൽ

${\displaystyle f'=0.}$^[10]

ഒരു സ്ഥിരവിലയുടെ ആരേഖം എപ്പോഴും തിരശ്ചീന രേഖ ആയിരിയ്ക്കും. ഇതിന്റ ആനതി 0 ആണല്ലോ.

• അവകലനത്തിന്റ രേഖീയത ( Sum rule):

${\displaystyle (\alpha f+\beta g)'=\alpha f'+\beta g'}$ എല്ലാ f, g എന്ന ഫലനങ്ങൾക്കും എല്ലാ ${\displaystyle \alpha }$ and ${\displaystyle \beta }$ എന്ന വാസ്തവികസംഖ്യകൾക്കും.^[10]

• '''ഗുണനനിയമം''' ( Product rule):

${\displaystyle (fg)'=f'g+fg'}$ എല്ലാ f, g എന്ന ഫലനങ്ങൾക്കും.^[10] ഇതിന്റെ ഒരു പ്രത്യേക കേസ് ആണ് ${\displaystyle \alpha }$ ഒരു സ്ഥിരവില ആകുമ്പോൾ ${\displaystyle (\alpha f)'=\alpha f'}$ എന്നത്, കാരണം

${\displaystyle (\alpha f)'=\alpha f'+f\alpha '}$

${\displaystyle f\alpha '=f\cdot 0=0}$, സ്ഥിരവില നിയമം മൂലം. അതുകൊണ്ട് ${\displaystyle (\alpha f)'=\alpha f'}$

• '''ഛേദനിയമം''' ( Quotient rule):

${\displaystyle \left({\frac {f}{g}}\right)'={\frac {f'g-fg'}{g^{2}}}}$ എല്ലാ f, g എന്ന ഫലനങ്ങൾക്കും g ≠ 0 ആയ എല്ലാ ഇന്പുട് വിലകൾക്കും.^[10]

• '''ശൃംഖലനിയമം''': ${\displaystyle f(x)=h(g(x))}$ ആണെങ്കിൽ,

${\displaystyle f'(x)=h'(g(x))\cdot g'(x).}$^[10]

ഇവ കൂടി കാണുക

• അവകലനം
• അവകലസമവാക്യം
• സമാകലനം