အာကာသ

အာကာသ (ခေါ်) ရပ်ဝန်း (သို့မဟုတ်) နေရာအကျယ်အဝန်းသဘော (အင်္ဂလိပ်: space) သည် အရာဝတ္ထု အစအနလေး၂ခု တစ်နေရာတည်း၊ တစ်မှတ်တည်း၌ ရှိမနေမှု ဖြစ်ပေါ်အောင် ဆောက်ရွက်သကဲ့သို့ ရှိသော သဘောတရား ဖြစ်သည်။ တနည်းအားဖြင့် ဆိုသော် အာကာသသည် နေရာအကျယ်အဝန်းသဘော ဖြစ်သည်။
ကျွန်ုပ်တို့ ကျွမ်းဝင်နေထိုင်ရာ လောကအကြောင်း ဖော်ပြသော ကံဇနဗေဒ(ရူပဗေဒ) အပိုင်းတွင် အရာဝတ္ထုနှင့်ဖြစ်ရပ်များထဲတွင် တည်နေရာနှင့် လားရာနှင့်ဆက်နွယ်ပြီး ဘောင်စည်းမျည်းမရှိသော သုံးဘက်မြင် (three dimensional) နေရာလွတ်ပင်ဖြစ်သည်။^[၁] “အာကာသ” ဟု ဆိုလိုက်လျှင် အချို့လူများက ကမ္ဘာ့အပြင်ဘက်ကိုချည်း ဆိုလိုသည် ထင်ကြသော်လည်း စင်စစ်အားဖြင့် ကံဇနေဗဒ(ရူပဗေဒ) ၌ “အာကာသ” (space) ဟူသည် နေရာအကျယ်အဝန်းသဘော အလုံးစုံကို ဆိုလိုပြီး “အချိန်” (time)ဟူသည့် သဘောတရားနှင့် တွဲဖက်လေ့လာဖွယ် ဖြစ်သည်။ ထို့ကြောင့် လေထုပြင်ပ လေဟာနယ် ဖြစ်သွားသည့် အပိုင်းကို ကွက်၍ ရည်ညွှန်းလိုလျှင် “အပြင်အာကာသ (outer space)” ဟု စနစ်တကျ ခွဲခြားသုံးနှုန်းနိုင်သည်။
သင်္ချာတွင်မူကား “အာကာသ(space)” ဆိုသည်မှာ ထို့ထက် ပိုမိုနက်နဲသွားသည်။

အာကာသတွင် တည်နေရာအားဖော်ပြရန်သုံးသည့် သုံးဒိုင်မင်းရှင်း Cartesian ကိုဩဒိနိတ်စနစ်

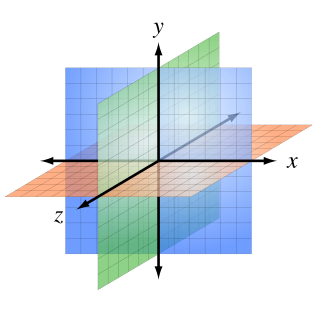
အာကာသ (ရပ်ဝန်း) သဘောတရားတစ်ခု၏ အဓိပ္ပါယ်မှာ အတိုင်းဆက သက်ရောက်ဖော်ပြမှ ပေါ်လွင်သည်။

ရုပ်ပိုင်းဆိုင်ရာ အာကာသအား လီနီယာ ဒိုင်မင်ရှင်း (linear dimensions) အဖြစ် စဉ်းစားသော်လည်းကံဇနပညာရှင်များသည် အချိန်ကိုပါထပ်ပေါင်းကာ လေးဘက်မြင်(four dimensional) အဖြစ် စဉ်းစားကြသည်။ ယင်းအား အာကာသအချိန် (spacetime)ဟု သိထားသည်။ အာကာသ အယူအဆသည် ခပ်သိမ်းလောကအားနားလည်ရန်အတွက် အခြေခံအရေးပါချက်ဖြစ်သည်။ အာကာသသည် စစ်စစ် ဗလနတ္ထိဟု ယခင် ပညာရှိကဝိများက တွေးဆခဲ့ကြလေသည်။ ယင်းတို့တွင် ပလေတို၊ အရစ္စတိုတယ်၊ ဆိုကရေးတီး၊ အစရှိသည်ဖြင့် ပါဝင်ကြသည်။ ဂန္ဓဝင် မက္ကင်းနစ်တွင် နယူတန်က အာကာသဆိုသည်မှာ ပုံသေဖြစ်ပြီး ယင်းတွင် မည်သည့်အရာဝတ္တု ရှိသည်ဖြစ်စေ အမြဲတမ်းနှင့် အမှီအခိုကင်းမဲ့သည်ဟု ဆိုလေသည်။^[၂] ၁၉ ရာစုနှင့် ၂ဝ ရာစုများတွင် အာကာသသည် ကွေးညွတ်နိုင်သည်ဟု တွေးဆခဲ့ကြလေသည်။ အိုင်းစတိုင်း၏ အထွေထွေနှိုင်းရသီအိုရီအရ အာကာသသည် အနီးအနားမှ ဒြပ်ဆွဲငင်အားများကြောင့် ပြောင်းလဲသည်ဟုဆိုသည်။^[၃]

သင်္ချာအားဖြင့် အာကာသ (သို့) ရပ်ဝန်း အမျိုးမျိုး

အတိုင်းဆဖော် ရပ်ဝန်းများ (အတိုင်းဆဖော် အာကာသများ)

ယူကလစ်ဒ် စပေ့စ်၏ အတိုင်းဆ(metric) ကိုသုံးသည့်အခါ ဤအမှတ်၂ခုကြား အကွာအဝေးသည် အစိမ်းမျဉ်းနှင့် ပြထားသည့်အတိုင်း ${\displaystyle 6{\sqrt {2}}\approx 8.49}$ ဟု ရပ်ဝန်းအတွင်း အတိုဆုံး လမ်းဖြောင့်ကို ရရှိ၏။ အနီ၊ အဝါ၊ အပြာတို့ဖြင့် ပြထားသည်မှာ တက္ကစီကားစပေ့စ် (taxicab space) ၏ အတိုင်းဆဖြင့် တွက်ထုတ်ထားသော အကွာအဝေးများ ဖြစ်ပြီး အလျား 12 ရှိ၏။

သင်္ချာတွင် အတိုင်းဆဖော် စပေ့စ် (သို့) အာကာသ (သို့) ရပ်ဝန်း ဆိုသည်မှာ ၎င်းအတွင်းပါဝင်သော အမှတ်တိုင်း၏ ကြား၌ အကွာအဝေးဟူသည့် သဘောတရားရှိသော အမှတ်အစုအအုံများ ဖြစ်လေ၏။ ထိုအကွာအဝေးသဘောကို ပေါ်လွင်စေသည့် တွက်ထုတ်ပုံကို အတိုင်းဆဟု ခေါ်သည်။^[၄]

ယူကလစ်ဒ် စပေ့စ်

သမားရိုးကျ တပြန့်ညီ ယူကလစ်ဒ် စပေ့စ် (flat Euclidean Space) ၏ အတိုင်းဆ တွက်ထုတ်နည်းမှာ ဤသို့ဖြစ်သည်။ $${\displaystyle d((x_{1},y_{1}),(x_{2},y_{2}))={\sqrt {(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}}.}$$ ဤသည်မှာ ကျောင်းသားအများစုနှင့်လည်း ရင်းနှီးသော ပိုက်သာဂိုရပ်စ်နည်းဖြင့် ထောင့်ဖြတ်အလျား တွက်ထုတ်သည့်သဖွယ်ပင် ဖြစ်သည်။

တက္ကစီကား စပေ့စ်

တက္ကစီကား စပေ့စ် (Taxicab Space) ၏ အတိုင်းဆ တွက်ထုတ်နည်းကို တွက်လျှင်မူ ဤသို့ ဖြစ်မည်။ $${\displaystyle ((x_{1},y_{1}),(x_{2},y_{2}))=|x_{2}-x_{1}|+|y_{2}-y_{1}|}$$ ဤအတိုင်းဆ (ဤ ကြားအကွာအဝေး တွက်ထုတ်နည်း)မှာ လေးထောင့်ကျသော မြို့ပြလမ်းကွက်များ၌ တက္ကစီကား မောင်းလျှင် သွားရမည့်အတိုင်း အကွာအဝေးကို အဖြေထုတ်ပေးသည်။

မင်ခေါ့ဗ်ရှကီး စပေ့စ်

မင်ခေါ့ဗ်ရှကီး စပေ့စ်^{(ဂျာမန်အမည် ဖြစ်၌ ဂျာမန်အသံထွက်ဖြင့်)} (Minkowski space) ၌မူ အမှတ်၂ခုတိုင်းကြားရှိ အကွာအဝေးသဘောကို ရှာထုတ်နိုင်ခြင်း မရှိသော်လည်း အချိန်ခြား (time-like) ဆက်စပ်မှုရှိသော အမှတ်၂ခု၏ အကွာအဝေးသဘောကိုမူ ဤသို့တွက်ထုတ်ရမည်ဟု ၎င်း၏ အတိုင်းဆက ဖှော်မျူလာ ပေး၏။ $${\displaystyle \left\|u\right\|={\sqrt {\eta (u,u)}}={\sqrt {c^{2}t^{2}-x^{2}-y^{2}-z^{2}}}}$$

အပိုင်းသဘော ရပ်ဝန်းများ

အပိုင်းသဘော (en:Topology) ဟူသော သင်္ချာအပိုင်း၌ ပါဝင်သော အပိုင်းသဘော ရပ်ဝန်း (en:topological space) ကိုကား ပိုမို ယေဘုယျကျနက်နဲသော မှတ်ရည်ချက်(axiom) များဖြင့် ဖွင့်ဆိုကြရသည်။