Ellipsoïde

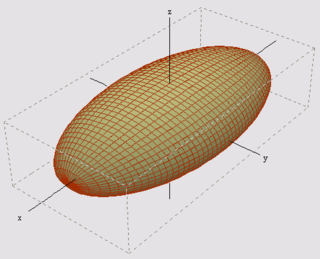
Een ellipsoïde is een lichaam met drie loodrechte symmetrievlakken. Een referentie-ellipsoïde is een omwentelingsellipsoïde, die een benadering voor de vorm van de Aarde vormt. Het oppervlak van een ellipsoïde is een kwadratisch oppervlak, maar wordt zelf ook ellipsoïde genoemd. Een ellipsoïde waarvan twee stralen gelijk zijn, is een sferoïde en sferoïden zijn een omwentelingslichaam. De drie doorsneden van een ellipsoïde met de genoemde symmetrievlakken zijn een ellips.

Ellipsoïde met ${\displaystyle (a,b,c)=(4,2,1)}$

Constructie van een oblate ellipsoïde

 ellips

 korte as

■ ongelijke ellipsoïde

■ prolate sferoïde

■ oblate sferoïde

De vergelijking van het oppervlak van een ellipsoïde in het cartesische coördinatenstelsel is:

${\displaystyle {x^{2} \over a^{2}}+{y^{2} \over b^{2}}+{z^{2} \over c^{2}}=1}$

${\displaystyle a,b}$ en ${\displaystyle c}$ leggen de vorm van de ellipsoïde vast:

• ${\displaystyle a={\tfrac {1}{2}}L}$ : helft van maximale lengte
• ${\displaystyle b={\tfrac {1}{2}}B}$ : helft van maximale breedte
• ${\displaystyle c={\tfrac {1}{2}}H}$ : helft van maximale hoogte

${\displaystyle a,b}$ en ${\displaystyle c}$ zijn groter dan nul. Wanneer ${\displaystyle a=b=c}$ gaat het om een bol.

Met ${\displaystyle a\geq b\geq c}$ zijn er de volgende mogelijkheden:

• ${\displaystyle a>b>c\ }$ een ongelijke ellipsoïde
• a ≠ b, a ≠ c en ${\displaystyle \ b=c\ }$ een sferoïde met de vorm van een sigaar, de prolate vorm
• ${\displaystyle a=b\ }$, a ≠ c en b ≠ c een sferoïde met de vorm van een pil, de oblate vorm
• ${\displaystyle a=b=c\ }$ een bol.

Elke ellipsoïde kan worden gevormd door een bol in een of twee richtingen langs orthogonale assen te verschalen. De ellips is een ontaarde vorm van een ellipsoïde.

Parametervergelijking

De volgende parametervergelijking stelt een ellips in het ${\displaystyle xy}$-vlak voor:

${\displaystyle [\ a\cos(\theta ),\ b\sin(\theta ),\ 0\ ]\ }$ met ${\displaystyle \theta }$ van 0 tot ${\displaystyle 2\pi }$,

na rotatie van deze ellips rond bijvoorbeeld de ${\displaystyle x}$-as wordt de parametervergelijking van een ellipsoïde

${\displaystyle [\ a\cos(\theta ),\ b\sin(\theta )\cos(\phi ),\ b\sin(\theta )\sin(\phi )\ ]\ }$ met ${\displaystyle \theta }$ en ${\displaystyle \phi }$ van 0 tot ${\displaystyle 2\pi }$.

Hiermee kan een prolate of oblate ellipsoïde worden geconstrueerd, maar geen ongelijke.

Volume

Het volume van een ellipsoïde is:

${\displaystyle V={\tfrac {4}{3}}\pi abc}$

Uitgaande van de maximale lengte, breedte en hoogte wordt het volume uitgedrukt door:

${\displaystyle V={\tfrac {1}{6}}\pi LBH\approx 0{,}524\ LBH}$

Oppervlakte

De oppervlakte is moeilijker om te berekenen:

${\displaystyle A=2\pi \left(c^{2}+{\frac {bc^{2}}{\sqrt {a^{2}-c^{2}}}}F(\theta ,m)+b{\sqrt {a^{2}-c^{2}}}E(\theta ,m)\right)}$

waarvoor geldt:

${\displaystyle m={\frac {a^{2}(b^{2}-c^{2})}{b^{2}(a^{2}-c^{2})}}}$

${\displaystyle \theta =\arcsin {\left(e\right)}}$

${\displaystyle e={\sqrt {1-{\frac {c^{2}}{a^{2}}}}}}$

en ${\displaystyle F(\theta ,m)}$ en ${\displaystyle E(\theta ,m)}$ zijn onvolledige elliptische integralen van de eerste en tweede orde.

Bij benadering levert dit de volgende relaties op:

platte ellips: ${\displaystyle =2\pi \left(ab\right)}$, factor twee vanwege bovenste plak en onderste plak

prolate ellipsoïde: ${\displaystyle \approx 2\pi \left(c^{2}+ac{\frac {\arcsin {\left(e\right)}}{e}}\right)}$

oblate ellipsoïde: ${\displaystyle \approx 2\pi \left(a^{2}+c^{2}{\frac {\operatorname {arctanh} {\left(e\right)}}{e}}\right)}$

ongelijke ellipsoïde: ${\displaystyle \approx 4\pi \left({\frac {a^{p}b^{p}+a^{p}c^{p}+b^{p}c^{p}}{3}}\right)^{1/p}}$

Voor ${\displaystyle p\approx 1,6075}$ geeft dit volgens Knud Thomsen een relatieve fout van maximaal 1,061%. Een waarde van ${\displaystyle p=8/5=1,6}$ is optimaal voor bijna sferische ellipsoïden, met volgens DW Cantrell een relatieve fout van maximaal.