Kwadratuur van de cirkel

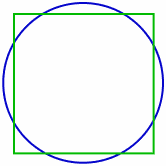
De kwadratuur van de cirkel is een wiskundig vraagstuk, dat voor het eerst is geformuleerd door meetkundigen in het oude Griekenland, onder meer Anaxagoras, Hippocrates en Archimedes. De vraag is of het mogelijk is om, met behulp van alleen passer en liniaal in een eindig aantal stappen een vierkant te construeren met dezelfde oppervlakte als een gegeven cirkel. De Griek Oenopides is wellicht de eerste geweest die de restricties omschreef van de toegestane middelen.

Vierkant en cirkel met dezelfde oppervlakte

Onmogelijkheid

Het vraagstuk dateert uit de tijd van de uitvinding van de meetkunde en heeft duizenden jaren lang veel wiskundigen beziggehouden. Pas in 1882 werd door Ferdinand von Lindemann onomstotelijk bewezen dat het niet kan, al had men al lang het idee dat het onmogelijk was.

Transcendentie van π {\displaystyle \pi }

Voor de oplossing van het vraagstuk van de kwadratuur van de cirkel met passer en liniaal is de constructie van een lijnstuk met lengte ${\displaystyle {\sqrt {\pi \ }}}$ en daarmee van π nodig. Al eerder was bewezen dat een constructie met passer en liniaal altijd kan worden 'vertaald' in het oplossen van een kwadratische vergelijking met hele coëfficiënten, en andersom is elke kwadratische vergelijking met gehele coëfficiënten om te zetten in een constructie met passer en liniaal. Maar in 1882 bewees Carl Louis Ferdinand von Lindemann dat ${\displaystyle \pi }$ een transcendent oftewel een niet-algebraïsch getal is. Omdat π niet kan optreden als oplossing van een algebraïsche vergelijking in het algemeen, laat staan van een kwadratische vergelijking, is de constructie van het gevraagde lijnstuk onmogelijk en daarmee ook de kwadratuur van de cirkel.

Als er een rationaal getal wordt gebruikt als benadering voor ${\displaystyle \pi }$, wordt het construeren van een vierkant met bij benadering dezelfde oppervlakte als van de gegeven cirkel wel mogelijk, afhankelijk van de gekozen waarde. Verscheidene wiskundigen hebben werkbare procedures laten zien, gebaseerd op verschillende benaderingen. Door het verruimen van de eisen heeft het vraagstuk wel oplossingen. Zo zijn er voor het vraagstuk binnen de niet-euclidische meetkunde wel oplossingen.

Gelijke vraagstukken

• Driedeling van de hoek
• Verdubbeling van de kubus
• Benaderingen van π door middel van meetkundige constructies

Mediabestanden

Zie de categorie Squaring the circle van Wikimedia Commons voor mediabestanden over dit onderwerp.