Hyperbolsk funksjon

Ein hyperbolsk funksjon er funksjonane sinh (sinus hyperbolicus), cosh (cosinus hyperbolicus), tanh (tangens hyperbolicus), coth (cotangens hyperbolicus), sech (secans hyperbolicus) og csch (cosecans hyperbolicus).

Her er e grunntalet i det naturlege logaritmesystemet.

Dei hyperbolske funksjonane har eigenskapar som er analoge med dei trigonometriske funksjonane. På same måte som ${\displaystyle \sin x}$ og ${\displaystyle \cos x}$ kan nyttast til å parametrisere ein sirkel, kan dei hyperbolske funksjonane ${\displaystyle \sinh x}$ og ${\displaystyle \cosh x}$ parametrisere ein hyperbel.

Standard algebraiske uttrykk

sinh, cosh og tanh

csch, sech og coth

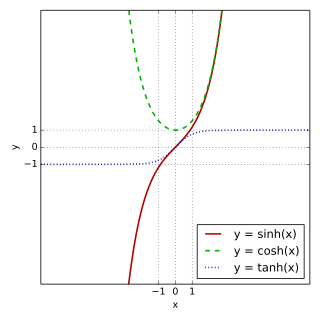
Dei hyperbolske funksjonane er :

• Hyperbolsk sinus:

${\displaystyle \sinh x={\frac {e^{x}-e^{-x}}{2}}={\frac {e^{2x}-1}{2e^{x}}}}$

• Hyperbolsk cosinus:

${\displaystyle \cosh x={\frac {e^{x}+e^{-x}}{2}}={\frac {e^{2x}+1}{2e^{x}}}}$

• Hyperbolsk tangens:

${\displaystyle \tanh x={\frac {\sinh x}{\cosh x}}={\frac {e^{x}-e^{-x}}{e^{x}+e^{-x}}}={\frac {e^{2x}-1}{e^{2x}+1}}}$

• Hyperbolsk cotangens:

${\displaystyle \coth x={\frac {\cosh x}{\sinh x}}={\frac {e^{x}+e^{-x}}{e^{x}-e^{-x}}}={\frac {e^{2x}+1}{e^{2x}-1}}}$

• Hyperbolsk secans:

${\displaystyle \operatorname {sech} \,x=\left(\cosh x\right)^{-1}={\frac {2}{e^{x}+e^{-x}}}={\frac {2e^{x}}{e^{2x}+1}}}$

• Hyperbolsk cosecans:

${\displaystyle \operatorname {csch} \,x=\left(\sinh x\right)^{-1}={\frac {2}{e^{x}-e^{-x}}}={\frac {2e^{x}}{e^{2x}-1}}}$

Hyperbolske funksjonane kan introduserast via imaginære sirkelvinklar:

• Hyperbolsk sinus:

${\displaystyle \sinh x=-{\rm {i}}\sin {\rm {i}}x\!}$

• Hyperbolsk cosinus:

${\displaystyle \cosh x=\cos {\rm {i}}x\!}$

• Hyperbolsk tangens:

${\displaystyle \tanh x=-{\rm {i}}\tan {\rm {i}}x\!}$

• Hyperbolsk cotangens:

${\displaystyle \coth x={\rm {i}}\cot {\rm {i}}x\!}$

• Hyperbolsk sekant:

${\displaystyle \operatorname {sech} \,x=\sec {{\rm {i}}x}\!}$

• Hyperbolsk cosecant:

${\displaystyle \operatorname {csch} \,x={\rm {i}}\,\csc \,{\rm {i}}x\!}$

der i er den imaginære eininga definert som i² = −1.

Dei komplekse formene i definisjonane over kjem frå Eulerformelen.

Nyttige forhold

${\displaystyle \sinh(-x)=-\sinh x\,\!}$

${\displaystyle \cosh(-x)=\cosh x\,\!}$

Dermed:

${\displaystyle \tanh(-x)=-\tanh x\,\!}$

${\displaystyle \coth(-x)=-\coth x\,\!}$

${\displaystyle \operatorname {sech} (-x)=\operatorname {sech} \,x\,\!}$

${\displaystyle \operatorname {csch} (-x)=-\operatorname {csch} \,x\,\!}$

Ein kan sjå at cosh x og sech x er jamne funksjonar, medan dei andre er odde funksjonar.

${\displaystyle \operatorname {arsech} \,x=\operatorname {arcosh} {\frac {1}{x}}}$

${\displaystyle \operatorname {arcsch} \,x=\operatorname {arsinh} {\frac {1}{x}}}$

${\displaystyle \operatorname {arcoth} \,x=\operatorname {artanh} {\frac {1}{x}}}$

Hyperbolsk sinus og cosinus tilfredsstiller identiteten

${\displaystyle \cosh ^{2}x-\sinh ^{2}x=1\,}$

som liknar den pythagoreiske trigonometriske identiteten. Ein har òg

${\displaystyle \tanh ^{2}x=1-\operatorname {sech} ^{2}x}$

${\displaystyle \coth ^{2}x=1+\operatorname {csch} ^{2}x}$

for dei andre funksjonane.

Den hyperbolske tangensen er løysinga til det ikkje-lineære grenseverdiproblemet^[1]:

${\displaystyle {\frac {1}{2}}f''=f^{3}-f\qquad$ ;\qquad f(0)=f'(\infty )=0}

Det kan visast at arealet under kurva til cosh x alltid er like bogelengda:^[2]

${\displaystyle {\text{areal}}=\int _{a}^{b}{\cosh {x}}\ dx=\int _{a}^{b}{\sqrt {1+\left({\frac {d}{dx}}\cosh {x}\right)^{2}}}\ dx={\text{bogelengd}}.}$

Inverse funksjonar som logaritmar

${\displaystyle \operatorname {arsinh} \,x=\ln \left(x+{\sqrt {x^{2}+1}}\right)}$

${\displaystyle \operatorname {arcosh} \,x=\ln \left(x+{\sqrt {x^{2}-1}}\right);x\geq 1}$

${\displaystyle \operatorname {artanh} \,x={\tfrac {1}{2}}\ln {\frac {1+x}{1-x}};\left|x\right|<1}$

${\displaystyle \operatorname {arcoth} \,x={\tfrac {1}{2}}\ln {\frac {x+1}{x-1}};\left|x\right|>1}$

${\displaystyle \operatorname {arsech} \,x=\ln {\frac {1+{\sqrt {1-x^{2}}}}{x}};0<x\leq 1}$

${\displaystyle \operatorname {arcsch} \,x=\ln \left({\frac {1}{x}}+{\frac {\sqrt {1+x^{2}}}{\left|x\right|}}\right)}$

Deriverte

${\displaystyle {\frac {d}{dx}}\sinh x=\cosh x\,}$

${\displaystyle {\frac {d}{dx}}\cosh x=\sinh x\,}$

${\displaystyle {\frac {d}{dx}}\tanh x=1-\tanh ^{2}x={\hbox{sech}}^{2}x=1/\cosh ^{2}x\,}$

${\displaystyle {\frac {d}{dx}}\coth x=1-\coth ^{2}x=-{\hbox{csch}}^{2}x=-1/\sinh ^{2}x\,}$

${\displaystyle {\frac {d}{dx}}\ {\hbox{csch}}\,x=-\coth x\ {\hbox{csch}}\,x\,}$

${\displaystyle {\frac {d}{dx}}\ {\hbox{sech}}\,x=-\tanh x\ {\hbox{sech}}\,x\,}$

${\displaystyle {\frac {d}{dx}}\,\operatorname {arsinh} \,x={\frac {1}{\sqrt {x^{2}+1}}}}$

${\displaystyle {\frac {d}{dx}}\,\operatorname {arcosh} \,x={\frac {1}{\sqrt {x^{2}-1}}}}$

${\displaystyle {\frac {d}{dx}}\,\operatorname {artanh} \,x={\frac {1}{1-x^{2}}}}$

${\displaystyle {\frac {d}{dx}}\,\operatorname {arcsch} \,x=-{\frac {1}{\left|x\right|{\sqrt {1+x^{2}}}}}}$

${\displaystyle {\frac {d}{dx}}\,\operatorname {arsech} \,x=-{\frac {1}{x{\sqrt {1-x^{2}}}}}}$

${\displaystyle {\frac {d}{dx}}\,\operatorname {arcoth} \,x={\frac {1}{1-x^{2}}}}$

Standardintegral

${\displaystyle \int \sinh ax\,dx=a^{-1}\cosh ax+C}$

${\displaystyle \int \cosh ax\,dx=a^{-1}\sinh ax+C}$

${\displaystyle \int \tanh ax\,dx=a^{-1}\ln(\cosh ax)+C}$

${\displaystyle \int \coth ax\,dx=a^{-1}\ln(\sinh ax)+C}$

${\displaystyle \int {\frac {du}{\sqrt {a^{2}+u^{2}}}}=\sinh ^{-1}\left({\frac {u}{a}}\right)+C}$

${\displaystyle \int {\frac {du}{\sqrt {u^{2}-a^{2}}}}=\cosh ^{-1}\left({\frac {u}{a}}\right)+C}$

${\displaystyle \int {\frac {du}{a^{2}-u^{2}}}=a^{-1}\tanh ^{-1}\left({\frac {u}{a}}\right)+C;u^{2}<a^{2}}$

${\displaystyle \int {\frac {du}{a^{2}-u^{2}}}=a^{-1}\coth ^{-1}\left({\frac {u}{a}}\right)+C;u^{2}>a^{2}}$

${\displaystyle \int {\frac {du}{u{\sqrt {a^{2}-u^{2}}}}}=-a^{-1}\operatorname {sech} ^{-1}\left({\frac {u}{a}}\right)+C}$

${\displaystyle \int {\frac {du}{u{\sqrt {a^{2}+u^{2}}}}}=-a^{-1}\operatorname {csch} ^{-1}\left|{\frac {u}{a}}\right|+C}$

Where C is the constant of integration.

Taylorrekkjer

Det er mogeleg å uttrykke funksjonane over som Taylorrekkje:

${\displaystyle \sinh x=x+{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}+{\frac {x^{7}}{7!}}+\cdots =\sum _{n=0}^{\infty }{\frac {x^{2n+1}}{(2n+1)!}}}$

Funksjonen sinh x har ei Taylorrekkje med berre odde eksponentar for x. Dermed er han ein oddefunksjon, som er −sinh x = sinh(−x), og sinh 0 = 0.

${\displaystyle \cosh x=1+{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}+{\frac {x^{6}}{6!}}+\cdots =\sum _{n=0}^{\infty }{\frac {x^{2n}}{(2n)!}}}$

Funksjonen cosh x har ei Taylorrekkje med berre jamne eksponentar for x. Derfor er han ein jamn funksjon, altså symmetrisk med omsyn til y-aksen. Summen av sinh- og cosh-rekkjene er ei uendeleg rekkje av eksponentialfunksjonen.

${\displaystyle \tanh x=x-{\frac {x^{3}}{3}}+{\frac {2x^{5}}{15}}-{\frac {17x^{7}}{315}}+\cdots =\sum _{n=1}^{\infty }{\frac {2^{2n}(2^{2n}-1)B_{2n}x^{2n-1}}{(2n)!}},\left|x\right|<{\frac {\pi }{2}}}$

${\displaystyle \coth x=x^{-1}+{\frac {x}{3}}-{\frac {x^{3}}{45}}+{\frac {2x^{5}}{945}}+\cdots =x^{-1}+\sum _{n=1}^{\infty }{\frac {2^{2n}B_{2n}x^{2n-1}}{(2n)!}},0<\left|x\right|<\pi }$ (Laurentrekkje)

${\displaystyle \operatorname {sech} \,x=1-{\frac {x^{2}}{2}}+{\frac {5x^{4}}{24}}-{\frac {61x^{6}}{720}}+\cdots =\sum _{n=0}^{\infty }{\frac {E_{2n}x^{2n}}{(2n)!}},\left|x\right|<{\frac {\pi }{2}}}$

${\displaystyle \operatorname {csch} \,x=x^{-1}-{\frac {x}{6}}+{\frac {7x^{3}}{360}}-{\frac {31x^{5}}{15120}}+\cdots =x^{-1}+\sum _{n=1}^{\infty }{\frac {2(1-2^{2n-1})B_{2n}x^{2n-1}}{(2n)!}},0<\left|x\right|<\pi }$ (Laurentrekkje)

der

${\displaystyle B_{n}\,}$ er det n-te Bernoullitalet

${\displaystyle E_{n}\,}$ er det n-te Eulertalet