Rozkład Benforda

Rozkład Benforda – rozkład prawdopodobieństwa występowania określonej pierwszej cyfry w wielu rzeczywistych danych statystycznych, np. dotyczących powierzchni jezior, danych z rocznika statystycznego, wartościach stałych fizycznych. Ogólnie rozkład ten sprawdza się w przypadku wielkości, które mogą przyjmować różne rzędy wielkości. Fakt częstego występowania tego rozkładu w obserwowanych danych zwany jest prawem Benforda.

Rozkład Benforda

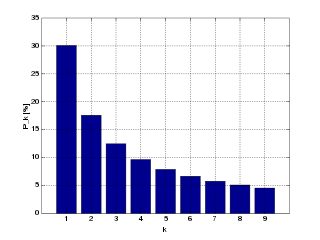
Prawdopodobieństwo wystąpienia cyfry ${\displaystyle k}$ to

${\displaystyle P_{k}=\log _{10}{\frac {k+1}{k}}=\log _{10}\left(1+{\frac {1}{k}}\right)}$

Przykład rozkładu wielkości, gdzie pierwsza cyfra spełnia w przybliżeniu prawo Benforda. Czerwony obszar odpowiada cyfrze 1, niebieski cyfrze 8.

Rozkłady wielkości, które obejmują tylko jeden rząd wielkości, zwykle nie spełniają prawa Benforda.

Rozkład Benforda jest stosowany do sprawdzania poprawności zeznań podatkowych bądź defraudacji, gdyż ludzie wpisując liczby tak, żeby wydawały się przypadkowe, nie są świadomi, że pewne cyfry występują częściej na pierwszej pozycji.

Częstotliwości występowania cyfr na pierwszej pozycji są przedstawione w tabeli poniżej.

Pierwsza cyfra	Częstość
1	30,1%
2	17,6%
3	12,5%
4	9,7%
5	7,9%
6	6,7%
7	5,8%
8	5,1%
9	4,6%

Historia

Charakterystyczna zależność została po raz pierwszy odnotowana w 1881 roku przez kanadyjskiego astronoma i matematyka Simona Newcomba. Przebywając w bibliotece United States Naval Observatory, Newcomb zauważył, że strony tablic logarytmicznych są brudniejsze na początku i coraz czystsze na dalszych kartkach. Wywnioskował, że korzystający z tablic logarytmicznych częściej szukają liczb rozpoczynających się od niższych cyfr – te znajdują się na początku tablic. Swoje odkrycie (bez dowodu ogólnej prawidłowości) opublikował na stronach American Journal of Mathematics^[1]. Jego artykuł nie spotkał się jednak z szerokim zainteresowaniem i niezwykle ciekawe zjawisko zostało zapomniane na 57 lat.

W 1938 roku Frank Benford, inżynier General Electric, nie zdając sobie sprawy z istnienia pracy Newcomba, dokonał tego samego odkrycia na podstawie stanu czystości tablic logarytmicznych. Zafascynowany tym zjawiskiem, Benford zaczął sprawdzać, czy jego teoria znajduje potwierdzenie również w innych zbiorach danych, m.in. w powierzchniach rzek, liczbach drukowanych w gazetach, czy nawet cenach. Wyniki swoich badań przedstawił w artykule wydrukowanym w Proceedings of the American Philosophical Society^[2]. Podobnie jak w artykule Newcomba, formalny dowód nie został przedstawiony.

Dowód twierdzenia podał w 1995 roku Theodore Hill^[3].

Przykłady zastosowania

Defraudacja Jamesa Nelsona

Zastosowanie rozkładu Benforda pomogło w wykryciu fałszerstw dokonanych przez Jamesa Nelsona, głównego księgowego i zarządzającego Arizona State Treasurer. W 1992 roku w miasteczku Wayne (Arizona, USA) został uznany za winnego zdefraudowania 1 878 687,58 dolarów. Dokonał tego wystawiając 23 fałszywe czeki.

• oszustwo rozpoczęło się małą kwotą (najmniejszą w całym procederze), przy czym kolejne kwoty fałszywych czeków stopniowo rosły,
• większość czeków wystawiono na kwotę poniżej 100 000 dolarów,
• wykrycie przestępstwa umożliwił rozkład pierwszych cyfr poszczególnych kwot.

Wybory prezydenckie w Iranie 2009

Boudewijn F. Roukema z toruńskiego Uniwersytetu Mikołaja Kopernika zaobserwował, iż rozkład pierwszych cyfr liczby głosów oddanych w wyborach w Iranie w 2009 roku w poszczególnych okręgach na kandydata małej partii opozycyjnej Mehdiego Karroubiego nie zgadza się z rozkładem Benforda – wśród pierwszych cyfr dwukrotnie częściej niż powinna pojawia się siódemka (poziom istotności 0,007). Anomalie występują w trzech z sześciu największych okręgów i są to właśnie okręgi, w których aktualny prezydent Mahmud Ahmadineżad miał proporcjonalnie wyższe poparcie niż w reszcie kraju^[4].

Jednakże statystycy Nate Silver^[5] i Andrew Gelman^[6] wyrazili sceptycyzm w kwestii znaczenia tego wyniku. Powszechnie uważa się, że odchylenie od rozkładu Benforda nie dowodzi, że doszło do oszustwa wyborczego^[7][8].

Zastosowanie podczas egzaminów

Badacze podejrzewali, że gdy poradzą studentom, aby na teście wielokrotnego wyboru z fizyki sugerowali się rozkładem Benforda, to osiągną oni nieprzeciętnie dobre wyniki. Tak się jednak nie stało, gdyż okazało się, że niepoprawne odpowiedzi również spełniają rozkład Benforda. Naukowcy nie wiedzą dlaczego^[9].

Fizyka kwantowa

Rozkład Benforda częściej daje poprawne wyniki zachowania przejść fazowych w kwantowych modelach XY niż inne teorie (wykorzystują one magnetyzację, splątanie kwantowe czy kwantową niezgodę („quantum discord”)^[10].

Zakres stosowalności

Rozkłady podlegające prawu Benforda

Niektóre dobrze znane nieskończone ciągi liczb całkowitych spełniają prawo Benforda dokładnie (w sensie granicznym, gdy uwzględnia się coraz więcej wyrazów ciągu). Należą do nich liczby Fibonacciego^[11][12], silnie^[13], potęgi liczby 2, a także niemal każdej innej liczby^[14].

Podobnie, niektóre procesy ciągłe również dokładnie spełniają prawo Benforda (w sensie granicznym, gdy proces trwa przez dłuższy czas). Przykładem jest proces wykładniczego wzrostu lub rozpadu: jeśli dana wielkość rośnie lub maleje wykładniczo w czasie, to odsetek czasu, przez jaki jej pierwsza cyfra ma określoną wartość, spełnia prawo Benforda asymptotycznie (czyli z rosnącą dokładnością w miarę trwania procesu).

Rozkłady niepodlegające prawu Benforda

Pierwiastki kwadratowe i odwrotności kolejnych liczb naturalnych nie podlegają temu rozkładowi^[15]. Liczby pierwsze w skończonym zakresie podlegają uogólnionemu rozkładowi Benforda, który dąży do rozkładu jednostajnego, w miarę jak rozmiar zakresu zbliża się do nieskończoności^[16]. Listy lokalnych numerów telefonów naruszają rozkład Benforda^[17]. Rozkład Benforda naruszają dane o wielkości populacje wszystkich miejsc, w których mieszka co najmniej 2500 osób z pięciu stanów USA, zgodnie ze spisami powszechnymi z lat 1960 i 1970, gdzie tylko 19% zaczynało od cyfry 1, ale 20% zaczynało od cyfry 2, ponieważ obcięcie przez uwzględnienie wartości co najmniej 2500 wprowadza zniekształcenie^[18]. Końcowe cyfry w badaniach histopatologicznych naruszają prawo Benforda ze względu na zaokrąglenia^[19].

Rozkłady, które nie obejmują kilku rzędów wielkości, nie spełniają rozkładu Benforda. Przykładami są wzrost, waga i wyniki testów IQ^[20][21].

Kryteria zgodności dla rozkładów Benforda

Zaproponowano szereg kryteriów, mających zastosowanie zwłaszcza do danych księgowych, w przypadku których można oczekiwać zastosowania prawa Benforda^[22].

Rozkłady, które mogą podlegać prawu Benforda:

• Gdy średnia jest większa od mediany i skośność jest dodatnia
• Liczby będące wynikiem matematycznej kombinacji liczb, np. ilość razy cena
• Dane na poziomie transakcji: np. wypłaty, sprzedaż

Rozkłady, od których nie oczekuje się podlegania prawu Benforda:

• Numery są nadawane sekwencyjnie: np. numery czeków, numery faktur
• Liczby są kształtowane przez ludzkie myśli: np. ceny ustalane na podstawie progów psychologicznych (9,99 USD)
• Konta z dużą liczbą wartości charakterystycznych dla prowadzonego biznesu, np. konta z kuponami na zwroty w wysokości 100 USD
• Konta z wbudowanym minimum lub maksimum
• Rozkłady, które nie obejmują rzędu wielkości liczb.

Twierdzenie o zgodności z rozkładem Benforda

Z matematycznego punktu widzenia prawo Benforda ma zastosowanie, jeśli badany rozkład spełnia „twierdzenie o zgodności z prawem Benforda”^[23]. Z wyprowadzenia tego twierdzenia wynika, że prawo Benforda jest spełnione wtedy, gdy transformata Fouriera logarytmu funkcji gęstości prawdopodobieństwa jest równa zeru dla wszystkich całkowitych wartości. W szczególności warunek ten jest spełniony, jeśli transformata Fouriera jest zerowa (lub pomijalnie mała) dla ${\displaystyle n\geqslant 1}$. Dzieje się tak, gdy rozkład jest „szeroki” (ponieważ szeroki rozkład implikuje wąską transformatę Fouriera). Smith podsumowuje to w następujący sposób:

Prawo Benforda jest spełnione przez rozkłady, które są szerokie w porównaniu z jednostkową odległością na skali logarytmicznej. Z kolei nie jest spełnione przez rozkłady, które są wąskie względem tej jednostki… Jeśli rozkład jest szeroki względem jednostkowej odległości na osi logarytmicznej, oznacza to, że rozpiętość analizowanego zbioru liczb jest znacznie większa niż dziesięć^[23].

W praktyce oznacza to, że aby rozkład spełniał prawo Benforda, dane muszą obejmować więcej niż jeden rząd wielkości.

Zobacz też

• prawo Zipfa