Najlepsze pytania
Chronologia
Czat
Perspektywa
Pochodna kierunkowa
Z Wikipedii, wolnej encyklopedii
Remove ads
Pochodna kierunkowa – pochodna funkcji wielu zmiennych obliczona w kierunku dowolnego wektora jednostkowego Pochodna kierunkowa jest uogólnieniem pojęcia pochodnej cząstkowej na dowolne kierunki, przy czym pochodne cząstkowe są tożsame z pochodnymi w kierunkach wektorów jednostkowych bazy układu współrzędnych.
Remove ads
Definicja pochodnej kierunkowej
Podsumowanie
Perspektywa

Niech dana będzie przestrzeń euklidesowa i zawarty w niej podzbiór otwarty
Pochodną kierunkową funkcji wzdłuż wektora jednostkowego w punkcie nazywamy granicę
zakładając, że granica ta istnieje.
Remove ads
Związek pochodnej kierunkowej z gradientem
Podsumowanie
Perspektywa

Twierdzenie:
Jeżeli istnieje gradient funkcji w punkcie (co oznacza, że jest różniczkowalna w )
to pochodna kierunkowa funkcji w kierunku wektora jest równa iloczynowi skalarnemu gradientu funkcji i wektora
Remove ads
Przykład
Podsumowanie
Perspektywa
(1) Niech będzie dana funkcja
(2) Gradient funkcji wynosi
(3) Pochodna kierunkowa funkcji w kierunku jednostkowego wektora dana jest zależnością
czyli
Remove ads
Twierdzenia
Podsumowanie
Perspektywa
Pochodna kierunkowa ma wiele własności identycznych jak zwykła pochodna. Wśród nich, dla funkcji i określonych w otoczeniu punktu w którym funkcje te są różniczkowalne, słuszne są reguły:
(1) reguła sumy
(2) reguła stałej: dla dowolnej stałej zachodzi
(3) reguła iloczynu (reguła Leibniza)
(4) reguła łańcuchowa: jeśli jest różniczkowalna w zaś jest różniczkowalna w to
Remove ads
Pochodna w kierunku wektora niejednostkowego
Podsumowanie
Perspektywa
(1) Definicja pochodnej w kierunku niejednostkowego i niezerowego wektora ma postać:
gdzie – długość wektora
(2) Twierdzenie
Gdy jest różniczkowalna w punkcie to
czyli pochodna ta jest identyczna jak dla wektora jednostkowego.
Uwaga:
Definicja pochodnej kierunkowej dla wektorów niejednostkowych jest niezgodna z notacją używaną w pozostałych działach matematyki, gdzie oczekuje się, iż pochodne algebry różniczkowej tworzą przestrzeń liniową.
Remove ads
Pochodna kierunkowa pochodnej Frécheta
Dla bardziej ogólnego przypadku pochodnej Frécheta pochodną kierunkową wyznacza wzór:
Remove ads
Związek z pochodną cząstkową
Jeśli jest bazą standardową w to pochodna kierunkowa funkcji wzdłuż wektora dla jest równa pochodnej cząstkowej względem zmiennej tzn.
gdzie
Remove ads
Rozmaitości różniczkowe
Podsumowanie
Perspektywa
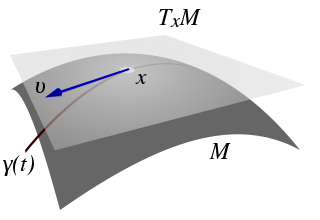
Jeżeli:
(1) jest funkcją określoną w otoczeniu punktu rozmaitości różniczkowej różniczkowalną w punkcie
(2) oznacza wektor styczny do rozmaitości w punkcie
(3) odwzorowanie generuje krzywą różniczkowalną taką że
- oraz
to pochodną kierunkową w punkcie wzdłuż wektora definiuje wzór
Tw. Dowodzi się, że pochodna ta nie zależy od wyboru krzywej
Remove ads
Przestrzenie liniowo-topologiczne
Bezpośrednim uogólnieniem pochodnej kierunkowej na lokalnie wypukłe przestrzenie liniowo-topologiczne (w tym przestrzenie Banacha) jest tzw. pochodna Gâteaux.
Różne oznaczenia pochodnej kierunkowej
Podsumowanie
Perspektywa
Istnieje wiele różnych oznaczeń pochodnej kierunkowej, np.
Remove ads
Zobacz też
Inne
Bibliografia
- Krzysztof Maurin: Analiza. Cz. I: Elementy. Warszawa: Państwowe Wydawnictwo Naukowe, 1976.
- Witold Kołodziej, Analiza matematyczna, Wydawnictwo Naukowe PWN, Warszawa 2009.
Linki zewnętrzne
- Eric W. Weisstein, Directional Derivative, [w:] MathWorld, Wolfram Research (ang.). [dostęp 2025-07-16].
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads
![{\displaystyle \mathbf {x} =[x_{1},\ldots ,x_{n}]\in \mathbb {R} ^{n}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/02c0f4af82d95209789484e8ed4a000a40a52cae)
![{\displaystyle \mathbf {u} =[u_{1},\ldots ,u_{n}].}](http://wikimedia.org/api/rest_v1/media/math/render/svg/cb19e6b4de0db9fc6bf73d115d42f6d68bef919e)




![{\displaystyle \mathbf {u} =[u_{1},\ldots ,u_{n}]\in \mathbb {R} ^{n}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/c6e58809810ebeac4f10476c302a91b6f0208546)
![{\displaystyle \mathbf {x} =[x_{1},\ldots ,x_{n}]\in A}](http://wikimedia.org/api/rest_v1/media/math/render/svg/6c58fdaf726c25e6bda74658191f791ae3e338d8)






![{\displaystyle \nabla f=\left[{\frac {\partial f}{\partial x_{1}}},\dots ,{\frac {\partial f}{\partial x_{n}}}\right],}](http://wikimedia.org/api/rest_v1/media/math/render/svg/c533dd0a1631b5d3656a14be7995ac509eda18da)


![{\displaystyle \nabla f(x,y)=\left[{\frac {\partial f(x,y)}{\partial x}},\ {\frac {\partial f(x,y)}{\partial y}}\right]=\left[2x+y,\ x-2y\right].}](http://wikimedia.org/api/rest_v1/media/math/render/svg/08e0894ea314cfd45de8bfabf7163472254a609f)
![{\displaystyle \mathbf {u} =\left[{\frac {1}{\sqrt {5}}},\ {\frac {2}{\sqrt {5}}}\right]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/60ac8df132dd3e3046259e342ac33b45612f08de)
![{\displaystyle \nabla _{\mathbf {u} }f(x,y)=\nabla f(x,y)\cdot \mathbf {u} =\left[2x+y,\ x-2y\right]\left[{\frac {1}{\sqrt {5}}},\ {\frac {2}{\sqrt {5}}}\right],}](http://wikimedia.org/api/rest_v1/media/math/render/svg/ba79d8da4bdbe6b6c5b6cff095731d6acd434d09)























![{\displaystyle \mathrm {x} =[x_{1},\dots ,x_{n}].}](http://wikimedia.org/api/rest_v1/media/math/render/svg/df1e28d089141e307fcbc10a0d1c05c4d4ee739e)









![{\displaystyle {\vec {\gamma }}\colon [-1,1]\to M}](http://wikimedia.org/api/rest_v1/media/math/render/svg/1c8b6f0431fdfb460e811bfff8289d27d25a08f7)





