Deltaedru

În geometrie un deltaedru este un poliedru ale cărui fețe sunt toate triunghiuri echilaterale. Numele este preluat din litera majusculă delta din alfabetul grec, (Δ), care are forma unui triunghi echilateral. Există infinit de multe deltaedre, toate având un număr par de fețe conform lemei care afirmă că orice graf are un număr par de noduri impare.^[1] Dintre acestea doar opt sunt convexe, având 4, 6, 8, 10, 12, 14, 16 și 20 de fețe.^[2] Numărul de fețe, laturi și vârfuri este dat mai jos pentru fiecare dintre cele opt deltaedre convexe.

Cel mai mare deltaedru strict convex este icosaedrul regulat

Acesta este un tetraedru trunchiat cu hexagoanele subdivizate în triunghiuri. Această figură nu este un deltaedru strict convex deoarece fețele coplanare nu sunt permise de definiție.

Cele opt deltaedre convexe

Există doar opt deltaedre strict convexe: trei sunt poliedre regulate, iar cinci sunt poliedre Johnson. Cele trei poliedre regulate convexe sunt poliedre platonice.

Deltaedre regulate
Imagine	Nume	Fețe	Laturi	Vârfuri	Configurațiile vârfurilor	Grup de simetrie
	tetraedru	4	6	4	4 × 33	Td, [3,3]
	octaedru	8	12	6	6 × 34	Oh, [4,3]
	icosaedru	20	30	12	12 × 35	Ih, [5,3]
Deltaedre Johnson
Imagine	Nume	Fețe	Laturi	Vârfuri	Configurațiile vârfurilor	Grup de simetrie
	bipiramidă triunghiulară	6	9	5	2 × 33 3 × 34	D3h, [3,2]
	bipiramidă pentagonală	10	15	7	5 × 34 2 × 35	D5h, [5,2]
	bisfenoid snub	12	18	8	4 × 34 4 × 35	D2d, [2,2]
	prismă triunghiulară triaugmentată	14	21	9	3 × 34 6 × 35	D3h, [3,2]
	bipiramidă pătrată giroalungită	16	24	10	2 × 34 8 × 35	D4d, [4,2]

În deltaedrul cu 6 fețe, unele vârfuri au gradul 3 și unele gradul 4. În deltaedrele cu 10, 12, 14 și 16 fețe, unele vârfuri au gradul 4 și unele gradul 5. Aceste cinci deltaedre neregulate aparțin clasei poliedrelor Johnson: poliedre convexe cu fețe poligonale regulate.

Deltaedrele își păstrează forma chiar dacă laturile sunt libere să se rotească în jurul vârfurilor lor, astfel încât unghiurile dintre laturi să fie fluide. Nu toate poliedrele au această proprietate: de exemplu, dacă se relaxează unele dintre unghiurile unui cub, cubul poate fi deformat într-o prismă pătrată oblică.

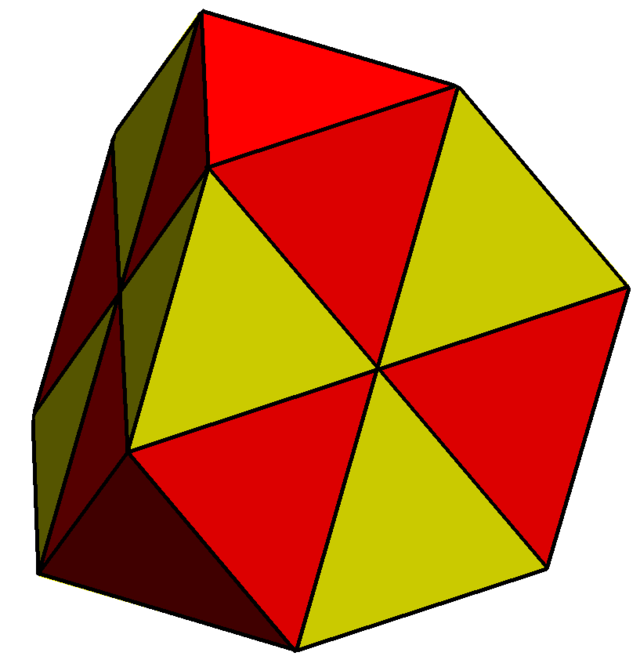
Nu există vreun deltaedru convex cu 18 fețe.^[3] Totuși, un icosaedru cu laturile contractate oferă un exemplu de octadecaedru care poate fi fie convex cu 18 fețe triunghiulare neregulate, fie realizat cu triunghiuri echilaterale, însă cu două seturi coplanare de trei triunghiuri.

Cazuri care nu sunt strict convexe

Există infinit de multe cazuri cu triunghiuri coplanare, permițând secțiuni ale pavărilor triunghiulare infinite. Dacă seturile de triunghiuri coplanare sunt considerate o singură față, se poate considera un set mai mic de fețe, laturi și vârfuri. Fețele triunghiulare coplanare pot fi îmbinate în fețe rombice, trapezoidale, hexagonale sau alte fețe poligonale echilaterale. Fiecare față trebuie să fie un polimino de triunghiuri convex, cum ar fi , , , , , , și , ...^[4]

Câteva exemple mai mici:

Deltaedre coplanare

Imagine	Nume	Fețe	Laturi	Vârfuri	Configurațiile vârfurilor	Grup de simetrie
	Octaedru augmentat Augmentare 1 tetr. + 1 octa.	10	15	7	1 × 33 3 × 34 3 × 35 0 × 36	C3v, [3]
		4 3	12
	Trapezoedru trigonal Augmentare 2 tetr. + 1 octa.	12	18	8	2 × 33 0 × 34 6 × 35 0 × 36	C3v, [3]
		6	12
	Augmentare 2 tetr. + 1 octa.	12	18	8	2 × 33 1 × 34 4 × 35 1 × 36	C2v, [2]
		2 2 2	11	7
	Trunchi triunghiular Augmentare 3 tetr. + 1 octa.	14	21	9	3 × 33 0 × 34 3 × 35 3 × 36	C3v, [3]
		1 3 1	9	6
	Octaedru alungit Augmentare 2 tetr. + 2 octa.	16	24	10	0 × 33 4 × 34 4 × 35 2 × 36	D2h, [2,2]
		4 4	12	6
	Tetraedru Augmentare 4 tetr. + 1 octa.	16	24	10	4 × 33 0 × 34 0 × 35 6 × 36	Td, [3,3]
		4	6	4
	Augmentare 3 tetr. + 2 octa.	18	27	11	1 × 33 2 × 34 5 × 35 3 × 36	D2h, [2,2]
		2 1 2 2	14	9
	Icosaedru cu fețe contractate	18	27	11	0 × 33 2 × 34 8 × 35 1 × 36	C2v, [2]
		12 2	22	10
	Bitrunchi triunghiular Augmentare 6 tetr. + 2 octa.	20	30	12	0 × 33 3 × 34 6 × 35 3 × 36	D3h, [3,2]
		2 6	15	9
	Cupolă triunghiulară Augmentare 4 tetr. + 3 octa.	22	33	13	0 × 33 3 × 34 6 × 35 4 × 36	C3v, [3]
		3 3 1 1	15	9
	Bipiramidă triunghiulară Augmentare 8 tetr. + 2 octa.	24	36	14	2 × 33 3 × 34 0 × 35 9 × 36	D3h, [3]
		6	9	5
	Antiprismă hexagonală	24	36	14	0 × 33 0 × 34 12 × 35 2 × 36	D6d, [12,2+]
		12 2	24	12
	Tetraedru trunchiat Augmentare 6 tetr. + 4 octa.	28	42	16	0 × 33 0 × 34 12 × 35 4 × 36	Td, [3,3]
		4 4	18	12
	Cuboctaedru tetrakis Octaedru Augmentare 8 tetr. + 6 octa.	32	48	18	0 × 33 12 × 34 0 × 35 6 × 36	Oh, [4,3]
		8	12	6

Forme neconvexe

Există un număr infinit de forme neconvexe.

Câteva exemple de deltaedre cu fețe autointersectate:

Marele icosaedru

• Marele icosaedru - un poliedru Kepler–Poinsot cu 20 de triunghiuri care se intersectează.

Alte deltaedre neconvexe pot fi generate prin adăugarea de piramide echilaterale pe fețele tuturor celor 5 poliedre platonice:

tetraedru triakis	hexaedru tetrakis	octaedru triakis (stella octangula)	dodecaedru pentakis	icosaedru triakis
12 triunghiuri	24 triunghiuri		60 triunghiuri

Alte augmentări ale tetraedrului:

Exemple: Tetraedre augmentate

8 triunghiuri	10 triunghiuri	12 triunghiuri

De asemenea, prin adăugarea pe fețe a unor piramide inversate:

• Dodecaedru excavat

Dodecaedru excavat	Un deltaedru toroidal
60 triunghiuri	48 triunghiuri