Radian

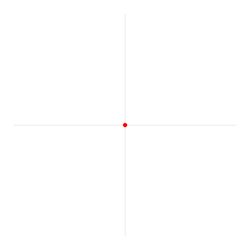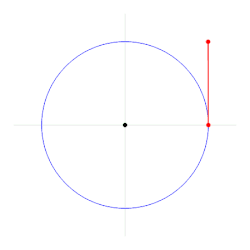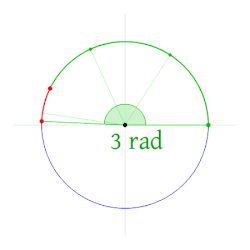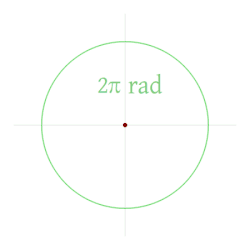
Un radian, având simbolul rad, este o unitate de măsură pentru măsura unghiurilor. Este unghiul care, având vârful în centrul unui cerc, intersectează pe circumferința acestuia un arc a cărui lungime este egală cu lungimea razei cercului. Măsura în radiani a unui unghi la centru este numeric egală cu lungimea arcului de cerc unitate (cu raza 1) corespunzător.

Radian
Un arc de cerc egal in lungime cu raza cercului corespunde unui unghi de 1 radian. Un cerc corespunde unui unghi de 2π radian.
Nume	radian
Mărime	Distanță unghiulară[1][2]
Unitatea în SI	1 radian
Modifică date / text

Un radian este egal 180°/π sau aproximativ 57,2958° sau 57°17'45.

Lungimea unui arc de cerc este egală cu raza înmulțită cu măsura în radiani a arcului.

Radianul face parte din Sistemul Internațional.

În matematică, unghiurile se exprimă de obicei în radiani, fără a scrie însă unitatea de măsură.

O rotație completă este rad 2π

Transformarea dintre radiani și grade

O diagramă folosită pentru transformarea între grade și radiani

Un radian este egal cu 180°/π. Pentru a transforma din radiani în grade, numărul radianilor se înmulțește cu 180/π. De exemplu:

${\displaystyle 1{\mbox{ rad}}=1\cdot {\frac {180^{\circ }}{\pi }}\approx 57,2958^{\circ }}$

${\displaystyle 2,5{\mbox{ rad}}=2.5\cdot {\frac {180^{\circ }}{\pi }}\approx 143,2394^{\circ }}$

${\displaystyle {\frac {\pi }{3}}{\mbox{ rad}}={\frac {\pi }{3}}\cdot {\frac {180^{\circ }}{\pi }}=60^{\circ }}$

Invers, pentru a transforma din grade în radiani, numărul gradelor se înmulțește cu π/180. De exemplu:

${\displaystyle 1^{\circ }=1\cdot {\frac {\pi }{180^{\circ }}}\approx 0.0175{\mbox{ rad}}}$

${\displaystyle 23^{\circ }=23\cdot {\frac {\pi }{180^{\circ }}}\approx 0.4014{\mbox{ rad}}}$

Istoric

Conceptul de radian ca unitate de măsură e atribuit de obicei lui Roger Cotes. Era cunoscut și matematicienilor arabo-persani ca de exemplu Al-Kashi.

Avantajele pentru a măsura în radiani

Some common angles, measured in radians. All the polygons are regular polygons.

În calcule și cele mai multe alte ramuri ale matematicii dincolo de geometrie practică, unghiurile sunt universal măsurate în radiani. Acest lucru se datorează faptului că radianii au o "naturalețe" matematică, care conduce la o formulare mai elegantă a unui număr de rezultate importante.

Statut dimensional

Este o unitate de măsură pentru o mărime adimensională deoarece este definit ca raport a două lungimi.

Vezi și

• Miliradian sau miime