Логнормальное распределение

Логнорма́льное распределе́ние (логарифмически-нормальное) в теории вероятностей — это двухпараметрическое семейство абсолютно непрерывных распределений. Если случайная величина имеет логнормальное распределение, то её логарифм имеет нормальное распределение.

Логнормальное
μ=0Плотность вероятности
μ=0Функция распределения
Обозначение	${\displaystyle \ln N(\mu ,\sigma ^{2})}$, ${\displaystyle LN(\mu ,\sigma ^{2})}$
Параметры	${\displaystyle \sigma >0}$ ${\displaystyle -\infty <\mu <\infty }$
Носитель	${\displaystyle x\in (0;+\infty )}$
Плотность вероятности	${\displaystyle \exp \left(-\left.\left[{\frac {\ln(x)-\mu }{\sigma }}\right]^{2}\right/2\right)\left/\left(x\sigma {\sqrt {2\pi }}\right)\right.}$
Функция распределения	${\displaystyle {\frac {1}{2}}+{\frac {1}{2}}\mathrm {erf} \left[{\frac {\ln(x)-\mu }{\sigma {\sqrt {2}}}}\right]}$
Математическое ожидание	${\displaystyle e^{\mu +\sigma ^{2}/2}}$
Медиана	${\displaystyle e^{\mu }}$
Мода	${\displaystyle e^{\mu -\sigma ^{2}}}$
Дисперсия	${\displaystyle (e^{\sigma ^{2}}\!\!-1)e^{2\mu +\sigma ^{2}}}$
Коэффициент асимметрии	${\displaystyle (e^{\sigma ^{2}}\!\!+2){\sqrt {e^{\sigma ^{2}}\!\!-1}}}$
Коэффициент эксцесса	${\displaystyle e^{4\sigma ^{2}}\!\!+2e^{3\sigma ^{2}}\!\!+3e^{2\sigma ^{2}}\!\!-6}$
Дифференциальная энтропия	${\displaystyle {\frac {1}{2}}+{\frac {1}{2}}\ln(2\pi \sigma ^{2})+\mu }$
Производящая функция моментов	${\displaystyle \operatorname {E} [X^{s}]=e^{s\mu +{\tfrac {1}{2}}s^{2}\sigma ^{2}}.}$
Характеристическая функция	${\displaystyle \sum _{n=0}^{\infty }{\frac {(it)^{n}}{n!}}e^{n\mu +n^{2}\sigma ^{2}/2}}$

Определение

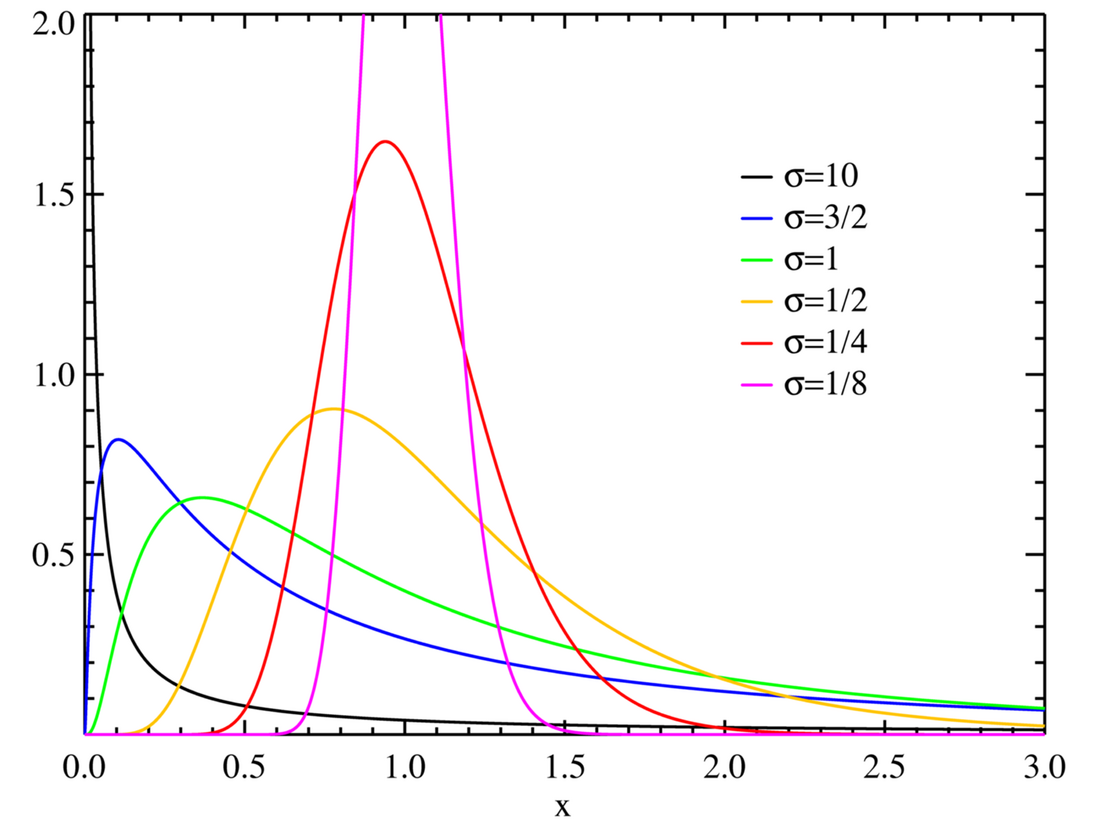
Пусть распределение случайной величины ${\displaystyle X}$ задаётся плотностью вероятности, имеющей вид^[1]:

$${\displaystyle f_{X}(x)={\frac {1}{x{\sqrt {2\pi }}\sigma }}e^{-(\ln x-\mu )^{2}/2\sigma ^{2}},}$$

где ${\displaystyle x>0,\;\sigma >0,\;\mu \in \mathbb {R} }$. Тогда говорят, что ${\displaystyle X}$ имеет логнормальное распределение с параметрами ${\displaystyle \mu }$ и ${\displaystyle \sigma }$^[1]. Пишут: ${\displaystyle X\sim \mathrm {LogN} (\mu ,\sigma ^{2})\ }$.

Моменты

Формула для ${\displaystyle k}$-го момента логнормальной случайной величины ${\displaystyle X}$ имеет вид^[1]:

${\displaystyle \mathbb {E} \left[X^{k}\right]=e^{k\mu +{\frac {k^{2}\sigma ^{2}}{2}}},\;k\in \mathbb {N} ,}$

откуда, в частности^[1]:

• ${\displaystyle \mathbb {E} [X]=e^{\mu +{\sigma ^{2} \over 2}}}$ — математическое ожидание,
• ${\displaystyle \mathrm {D} [X]=\left(e^{\sigma ^{2}}-1\right)e^{2\mu +\sigma ^{2}}}$ — дисперсия,
• Асимметрия всегда положительна.

Любые нецентральные моменты n-мерного совместного логнормального распределения могут быть вычислены по простой формуле^{[источник не указан 519 дней]}:

${\displaystyle \alpha _{n}=e^{(\mu ,n)+{\frac {1}{2}}(n,\Sigma n)}}$, где ${\displaystyle \mu }$ и ${\displaystyle \Sigma }$ — параметры многомерного совместного распределения. ${\displaystyle n}$ — вектор, компоненты которого задают порядок момента. (Например, в двухмерном случае, ${\displaystyle n=(2,0)}$ — второй нецентральный момент первой компоненты, ${\displaystyle n=(1,1)}$ — смешанный второй момент). Круглые скобки обозначают скалярное произведение.

Свойства логнормального распределения

• Если ${\displaystyle X_{1},\ldots ,X_{n}}$ — независимые логнормальные случайные величины, такие что ${\displaystyle X_{i}\sim \mathrm {LogN} (\mu ,\sigma _{i}^{2})}$, то их произведение также логнормально^[1]:

  ${\displaystyle Y=\prod \limits _{i=1}^{n}X_{i}\sim \mathrm {LogN} \left(n\mu ,\sum \limits _{i=1}^{n}\sigma _{i}^{2}\right)}$.

Связь с другими распределениями

• Если ${\displaystyle X\sim \mathrm {LogN} (\mu ,\sigma ^{2})\ }$, то ${\displaystyle Y=\ln(X)\sim \mathrm {N} (\mu ,\sigma ^{2})\ }$.

И наоборот, если ${\displaystyle Y\sim \mathrm {N} (\mu ,\sigma ^{2})\ }$, то ${\displaystyle X=\exp(Y)\sim \mathrm {LogN} (\mu ,\sigma ^{2})\ }$.

Моделирование логнормальных случайных величин

Для моделирования обычно используется связь с нормальным распределением. Поэтому, достаточно сгенерировать нормально распределённую случайную величину, например, используя преобразование Бокса — Мюллера, и вычислить её экспоненту^{[источник не указан 519 дней]}.

Вариации и обобщения

Одним из возможных обобщений является усечённое логнормальное распределение, описываемое плотностью вероятности^[2]:

${\displaystyle f_{X}(x)={\frac {1}{(x-\gamma ){\sqrt {2\pi }}\sigma }}e^{-(\ln(x-\gamma )-\mu )^{2}/2\sigma ^{2}},}$

где ${\displaystyle 0<\gamma <x}$.

Приложения

Логнормальное распределение часто возникает в природе и широко используется для описания разных параметров в различных дисциплинах. Например, в медицине его могут применять для инкубационных периодов случаев какого-либо заболевания, в геологии — для концентрации редких элементов в горных породах, в лингвистике — для количества слов в предложениях. Распределение частиц по размерам в разных системах также часто оказывается близко к логнормальному^[1][3]. Однако здесь есть исключения, например, распределение астероидов по размерам в Солнечной системе подчиняется степенному закону^[4].