Размерность графа

Размерность графа — наименьшее целое n такое, что существует «классическое представление» графа в евклидовом пространстве размерности n с единичными длинами рёбер.

Размерность графа Петерсена равна 2.

В классическом представлении все вершины должны быть различны, но рёбра могут пересекаться^[1].

Размерность графа G записывается как ${\displaystyle \dim G}$.

Например, граф Петерсена может быть нарисован с единичными рёбрами в ${\displaystyle E^{2}}$, но не в ${\displaystyle E^{1}}$, его размерность поэтому равна 2 (см. рисунок справа).

Концепцию предложили в 1965 году Пал Эрдёш, Фрэнк Харари и Уильям Татт^[2]. Она обобщает концепцию графа единичных расстояний для размерностей более 2.

Примеры

Для 4 равноудалённых точек нужна размерность 3.

Полный граф

В худшем случае каждая пара вершин соединена, что даёт полный граф.

Для погружения полного графа ${\displaystyle K_{n}}$ со всеми рёбрами единичной длины нам необходимо евклидово пространство размерности ${\displaystyle n-1}$^[3]. Например, нужно двухмерное пространство для погружения ${\displaystyle K_{3}}$ (равносторонний треугольник) и трёхмерное для погружения ${\displaystyle K_{4}}$ (правильный тетраэдр) как показано справа.

${\displaystyle \dim K_{n}=n-1}$

Другими словами, размерность полного графа совпадает с размерностью симплекса, имеющего то же самое число вершин.

Полный двудольный граф ${\displaystyle K_{4,2}}$ нарисованный в евклидовом 3-мерном пространстве.

Полные двудольные графы

Граф-звезда, нарисованный на плоскости с рёбрами единичной длины.

Все звёзды ${\displaystyle K_{m,1}}$ для ${\displaystyle m\geqslant 3}$ имеют размерность 2 как показано на рисунке слева. Для звёзд с m равным 1 или 2 достаточна размерность 1.

Полный двудольный граф ${\displaystyle K_{m,2}}$ для ${\displaystyle m\geqslant 3}$ может быть нарисован как на рисунке справа путём расположения m вершин на окружности, радиус которой меньше единицы, другие две точки располагаем по обеим сторонам от плоскости окружности на соответствующем расстоянии. ${\displaystyle K_{2,2}}$ имеет размерность 2, так как он может быть нарисован на плоскости в виде ромба.

Размерность полного двудольного графа ${\displaystyle K_{m,n}}$ для ${\displaystyle m\geqslant 3}$ и ${\displaystyle n\geqslant 3}$ равна 4. Доказательство Чтобы показать, что 4-мерного пространства достаточно, как и в предыдущем случае используем окружности. Обозначим координаты 4-мерного пространства ${\displaystyle w,x,y,z}$. Расположим один набор вершин произвольно на окружности ${\displaystyle w^{2}+x^{2}=a,y=0,z=0}$, где ${\displaystyle 0<a<1}$, а другой произвольно на окружности ${\displaystyle y^{2}+z^{2}=1-a,w=0,x=0}$. Мы видим, что расстояние между любой вершиной из первого множества и любой вершиной из второго множества равно ${\displaystyle {\sqrt {w^{2}+x^{2}+y^{2}+z^{2}}}={\sqrt {a+1-a}}=1}$. Мы также можем показать, что подграф ${\displaystyle K_{3,3}}$ не позволяет такого представления в размерности, меньшей 4: Если такое представление существует, то три точки ${\displaystyle A_{1}}$, ${\displaystyle A_{2}}$ и ${\displaystyle A_{3}}$ лежат на единичной сфере с центром ${\displaystyle B_{1}}$. Аналогично, они лежат на единичных сферах с центрами ${\displaystyle B_{2}}$ и ${\displaystyle B_{3}}$. Первые две сферы должны пересекаться по окружности, в точке или не пересекаться вообще. Для размещения трёх различных точек ${\displaystyle A_{1}}$, ${\displaystyle A_{2}}$ и ${\displaystyle A_{3}}$ мы должны предположить пересечение по окружности. Либо эта окружность лежит полностью на третьей единичной сфере, откуда следует, что третья сфера совпадает с одной из первых двух, так что ${\displaystyle B_{1}}$, ${\displaystyle B_{2}}$ и ${\displaystyle B_{3}}$ не все различны. Если же окружности не пересекаются по окружности, они пересекаются с третьей сферой не более чем в двух точках, а этого недостаточно, чтобы расположить три точки ${\displaystyle A_{1}}$, ${\displaystyle A_{2}}$ и ${\displaystyle A_{3}}$.

В итоге:

${\displaystyle \dim K_{m,n}=1,2,3,4}$, в зависимости от значений m и n.

Размерность и хроматическое число

Размерность графа G всегда меньше или равна удвоенному хроматическому числу:

${\displaystyle \dim G\leqslant 2\,\chi (G)}$

Доказательство

Это доказательство использует окружности.

Обозначим через n хроматическое число графа G и назначим целые числа ${\displaystyle (1..n)}$ для n цветов. В ${\displaystyle 2n}$-мерном евклидовом пространстве с размерностями, обозначенными через ${\displaystyle x_{1},x_{2},..x_{2n}}$, мы располагаем все вершины цвета n произвольно на окружности, заданной формулой ${\displaystyle x_{2n-2}^{2}+x_{2n-1}^{2}=1/2,\quad x_{i}|(i\neq 2{n-2},i\neq 2{n-1})=0}$.

Тогда расстояние от вершины цвета p до вершины цвета q задаётся формулой ${\displaystyle {\sqrt {x_{2p-2}^{2}+x_{2p-1}^{2}+x_{2q-2}^{2}+x_{2q-1}^{2}}}={\sqrt {1/2+1/2}}=1}$.

Евклидова размерность

Колесо с одной удалённой спицей имеет размерность 2.

То же самое колесо имеет евклидову размерность 3.

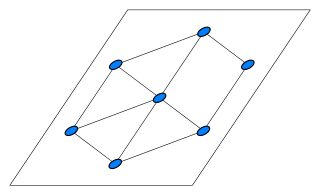
Определение размерности графа, данное выше, утверждает для n-минимального представления:

• если две вершины графа G связаны ребром, они должны быть на расстоянии единица;
• однако две вершины на расстоянии единица не обязательно должны быть соединены ребром.

Это определение отвергается некоторыми авторами. Другое определение предложил в 1991 годуАлександр Сойфер^[англ.], которое он называет евклидовой размерностью графа^[4]. Перед этим в 1980 году Пал Эрдёш и Миклош Шимонович^[англ.] уже предложили это же определение под названием истинная размерность^[5]. По этому определению n-минимальное представление — это то, в котором две вершины графа соединены тогда и только тогда, когда их представление находится на расстоянии 1.

Рисунок напротив показывает разницу между этими определениями для случая колеса, имеющего центральную вершину и шесть периферийных вершин с удалённой одной спицей. Представление графа на плоскости позволяет двум вершинам находиться на расстоянии 1, но при этом они не соединены.

Мы записываем евклидово расстояние как ${\displaystyle \operatorname {Edim} G}$. Оно никогда не меньше расстояния, определённого выше:

${\displaystyle \dim G\leqslant \operatorname {Edim} G}$

Евклидова размерность и максимальная степень

Пал Эрдёш и Миклош Шимонович доказали в 1980 году следующий результат^[5]:

Евклидова размерность графа G не больше чем его удвоенная максимальная степень + 1:

${\displaystyle \operatorname {Edim} G\leqslant 2\,\Delta (G)+1}$

Вычислительная сложность

Задача NP-трудна, и более конкретно, для экзистенциальной теории вещественных чисел полна задача определения, больше или нет размерность или евклидова размерность данного графа заданного значения. Задача остаётся трудной даже для проверки, равна ли двум размерность или евклидова размерность^[6].